Question Number 98616 by bemath last updated on 15/Jun/20

Answered by bobhans last updated on 15/Jun/20
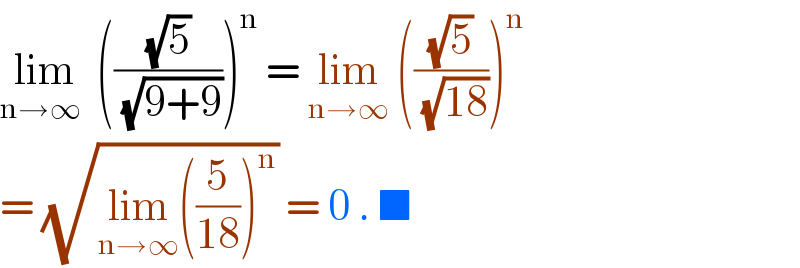
$$\underset{\mathrm{n}\rightarrow\infty\:} {\mathrm{lim}}\:\left(\frac{\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{9}+\mathrm{9}}}\right)^{\mathrm{n}} \:=\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{18}}}\right)^{\mathrm{n}} \\ $$$$=\:\sqrt{\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{5}}{\mathrm{18}}\right)^{\mathrm{n}} }\:=\:\mathrm{0}\:.\:\blacksquare \\ $$
Answered by mathmax by abdo last updated on 15/Jun/20
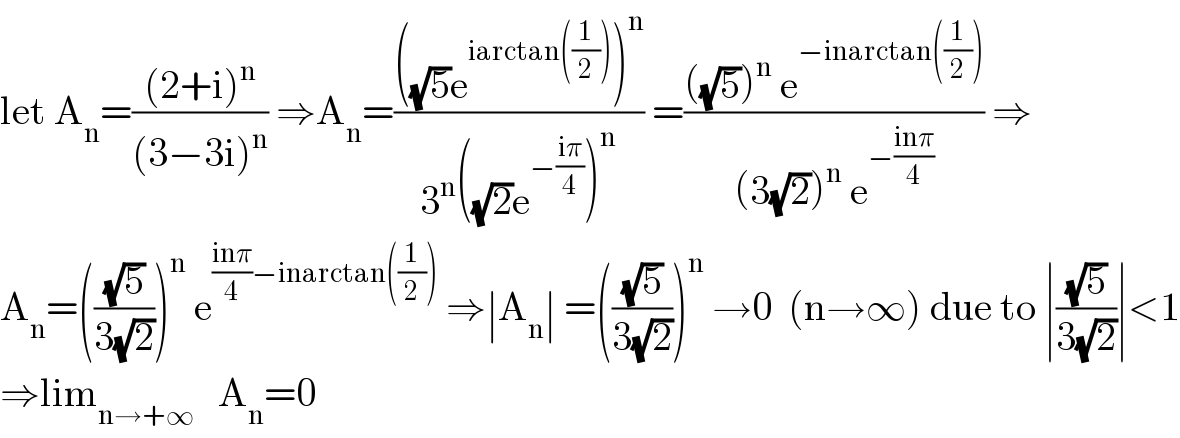
$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\frac{\left(\mathrm{2}+\mathrm{i}\right)^{\mathrm{n}} }{\left(\mathrm{3}−\mathrm{3i}\right)^{\mathrm{n}} }\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\frac{\left(\sqrt{\mathrm{5}}\mathrm{e}^{\mathrm{iarctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \right)^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}} \left(\sqrt{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{n}} }\:=\frac{\left(\sqrt{\mathrm{5}}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{inarctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} }{\left(\mathrm{3}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \:\mathrm{e}^{−\frac{\mathrm{in}\pi}{\mathrm{4}}} }\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{3}\sqrt{\mathrm{2}}}\right)^{\mathrm{n}} \:\mathrm{e}^{\frac{\mathrm{in}\pi}{\mathrm{4}}−\mathrm{inarctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \:\Rightarrow\mid\mathrm{A}_{\mathrm{n}} \mid\:=\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{3}\sqrt{\mathrm{2}}}\right)^{\mathrm{n}} \:\rightarrow\mathrm{0}\:\:\left(\mathrm{n}\rightarrow\infty\right)\:\mathrm{due}\:\mathrm{to}\:\mid\frac{\sqrt{\mathrm{5}}}{\mathrm{3}\sqrt{\mathrm{2}}}\mid<\mathrm{1} \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\:\mathrm{A}_{\mathrm{n}} =\mathrm{0} \\ $$
