Question Number 98621 by abony1303 last updated on 15/Jun/20
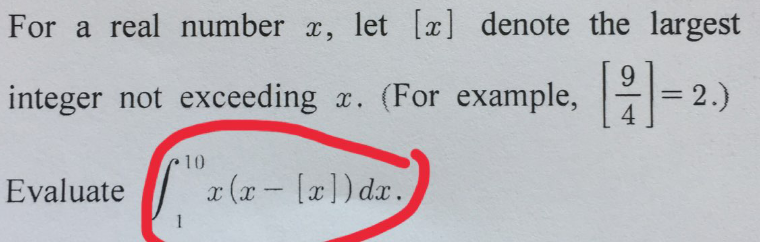
Commented by abony1303 last updated on 15/Jun/20

$$\mathrm{pls}\:\mathrm{help} \\ $$
Answered by mr W last updated on 15/Jun/20
![let x=n+t with 0≤t<1 ∫_1 ^(10) x(x−[x])dx =Σ_(n=1) ^9 ∫_n ^(n+1) x(x−[x])dx =Σ_(n=1) ^9 ∫_0 ^1 (n+t)tdt =Σ_(n=1) ^9 ((n/2)+(1/3)) =(1/2)×((9×10)/2)+(9/3) =((51)/2)](https://www.tinkutara.com/question/Q98630.png)
$${let}\:{x}={n}+{t}\:{with}\:\mathrm{0}\leqslant{t}<\mathrm{1} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{10}} {x}\left({x}−\left[{x}\right]\right){dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\int_{{n}} ^{{n}+\mathrm{1}} {x}\left({x}−\left[{x}\right]\right){dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \left({n}+{t}\right){tdt} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{9}} {\sum}}\left(\frac{{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{9}×\mathrm{10}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{51}}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 15/Jun/20
![I =∫_1 ^(10) x(x−[x])dx ⇒I =∫_1 ^(10) x^2 dx−∫_1 ^(10) x[x]dx ∫_1 ^(10) x^2 dx =[(x^3 /3)]_1 ^(10) =(1/3)(10^3 −1) =((999)/3) =333 ∫_1 ^(10) x[x] =Σ_(k=1) ^9 ∫_k ^(k+1) kx dx =Σ_(k=1) ^9 k((((k+1)^2 )/2)−(k^2 /2)) =(1/2)Σ_(k=1) ^9 k(2k+1) =Σ_(k=1) ^9 k^2 +(1/2)Σ_(k=1) ^9 k =((9(9+1)(2.9+1))/6) +(1/2)((9(9+1))/2) =((9×10×19)/6) +(1/4)×9×10 =3×5×19 +((45)/2) =15×19 +((45)/2) =285+((45)/2) ⇒ I =333−285−((45)/2) =48−((45)/2) =((96−45)/2) =((51)/2)](https://www.tinkutara.com/question/Q98639.png)
$$\mathrm{I}\:=\int_{\mathrm{1}} ^{\mathrm{10}} \:\mathrm{x}\left(\mathrm{x}−\left[\mathrm{x}\right]\right)\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{1}} ^{\mathrm{10}} \mathrm{x}^{\mathrm{2}} \:\mathrm{dx}−\int_{\mathrm{1}} ^{\mathrm{10}} \:\mathrm{x}\left[\mathrm{x}\right]\mathrm{dx} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{10}} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{dx}\:=\left[\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{1}} ^{\mathrm{10}} \:=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{10}^{\mathrm{3}} −\mathrm{1}\right)\:=\frac{\mathrm{999}}{\mathrm{3}}\:=\mathrm{333} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{10}} \:\mathrm{x}\left[\mathrm{x}\right]\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{9}} \:\int_{\mathrm{k}} ^{\mathrm{k}+\mathrm{1}} \mathrm{kx}\:\mathrm{dx}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{9}} \:\mathrm{k}\left(\frac{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{9}} \mathrm{k}\left(\mathrm{2k}+\mathrm{1}\right)\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{9}} \:\mathrm{k}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{9}} \:\mathrm{k} \\ $$$$=\frac{\mathrm{9}\left(\mathrm{9}+\mathrm{1}\right)\left(\mathrm{2}.\mathrm{9}+\mathrm{1}\right)}{\mathrm{6}}\:+\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{9}\left(\mathrm{9}+\mathrm{1}\right)}{\mathrm{2}}\:=\frac{\mathrm{9}×\mathrm{10}×\mathrm{19}}{\mathrm{6}}\:+\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{9}×\mathrm{10} \\ $$$$=\mathrm{3}×\mathrm{5}×\mathrm{19}\:+\frac{\mathrm{45}}{\mathrm{2}}\:=\mathrm{15}×\mathrm{19}\:+\frac{\mathrm{45}}{\mathrm{2}}\:=\mathrm{285}+\frac{\mathrm{45}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{333}−\mathrm{285}−\frac{\mathrm{45}}{\mathrm{2}}\:=\mathrm{48}−\frac{\mathrm{45}}{\mathrm{2}}\:=\frac{\mathrm{96}−\mathrm{45}}{\mathrm{2}}\:=\frac{\mathrm{51}}{\mathrm{2}} \\ $$$$ \\ $$
