Question Number 98675 by Algoritm last updated on 15/Jun/20
Commented by Algoritm last updated on 16/Jun/20
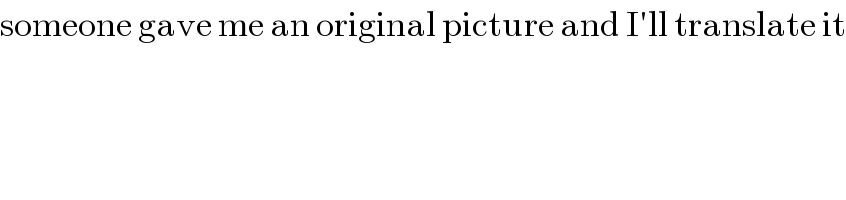
$$\mathrm{someone}\:\mathrm{gave}\:\mathrm{me}\:\mathrm{an}\:\mathrm{original}\:\mathrm{picture}\:\mathrm{and}\:\mathrm{I}'\mathrm{ll}\:\mathrm{translate}\:\mathrm{it} \\ $$
Commented by mr W last updated on 15/Jun/20

$${no}\:{further}\:{information}? \\ $$$${then}\:{you}\:{can}'{t}\:{determine}\:{x}\:{uniquely}. \\ $$
Commented by mr W last updated on 15/Jun/20

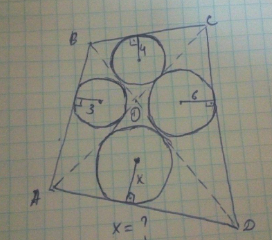
$${i}\:{understand}\:{the}\:{question}\:{well}.\:{your} \\ $$$${machine}\:{translation}\:{makes}\:{the}\:{thing} \\ $$$${even}\:{more}\:{unclear}.\:{please}\:{delete}\:{it}! \\ $$$$ \\ $$$${as}\:{i}\:{said}\:{you}\:{can}\:{not}\:{determine}\:{the} \\ $$$${radius}\:{of}\:{the}\:{fourth}\:{circle}\:{if}\:{only} \\ $$$${the}\:{radii}\:{of}\:{other}\:{three}\:{circles}\:{are} \\ $$$${given}. \\ $$$$ \\ $$$${ONLY}\:{if}\:{the}\:{quadrilateral}\:{is}\:{a}\:{so}− \\ $$$${called}\:{tangential}\:{quadrilateral},\:{then} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow{x}=\mathrm{4} \\ $$$$ \\ $$$${a}\:{tangential}\:{quadrilateral}\:{is}\:{a} \\ $$$${quadrilateral}\:{whose}\:{sides}\:{all} \\ $$$${tangent}\:{the}\:{same}\:{circle}. \\ $$
Commented by Algoritm last updated on 16/Jun/20

Commented by Algoritm last updated on 16/Jun/20
Commented by Algoritm last updated on 16/Jun/20
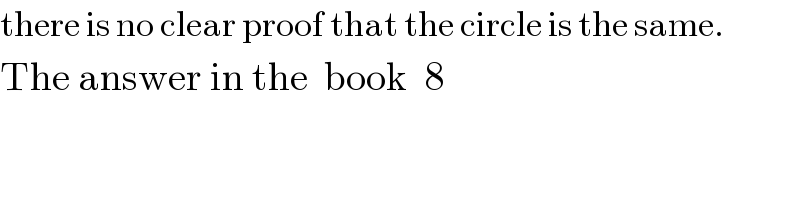
$$\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{clear}\:\mathrm{proof}\:\mathrm{that}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}. \\ $$$$\mathrm{The}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{the}\:\:\mathrm{book}\:\:\mathrm{8} \\ $$
Commented by Algoritm last updated on 16/Jun/20

$$\mathrm{Mr}\:\:\mathrm{W}\:\:\: \\ $$
Commented by mr W last updated on 16/Jun/20

$${i}\:{have}\:{said}:\:{there}\:{is}\:{no}\:{unique} \\ $$$${solution}\:{for}\:{the}\:{radius}\:{of}\:{the}\:{fourth} \\ $$$${circle}. \\ $$
Commented by mr W last updated on 16/Jun/20

$${question}\:{is}\:{wrong}\:{or}\:{there}\:{is}\:{additional} \\ $$$${information}.\:{please}\:{translate}\:{the} \\ $$$${question}\:{exactly}\:{into}\:{english}. \\ $$
Commented by mr W last updated on 16/Jun/20

