Question Number 98808 by bemath last updated on 16/Jun/20
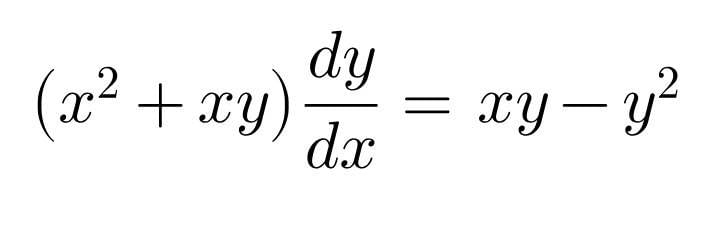
Answered by john santu last updated on 16/Jun/20
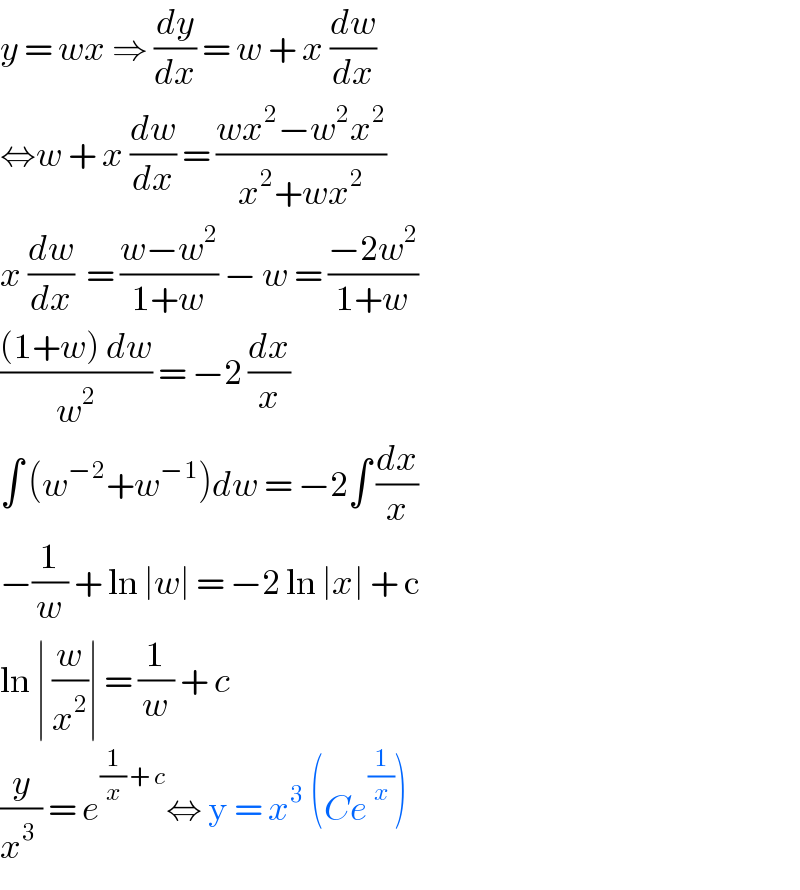
$${y}\:=\:{wx}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:{w}\:+\:{x}\:\frac{{dw}}{{dx}} \\ $$$$\Leftrightarrow{w}\:+\:{x}\:\frac{{dw}}{{dx}}\:=\:\frac{{wx}^{\mathrm{2}} −{w}^{\mathrm{2}} {x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{wx}^{\mathrm{2}} } \\ $$$${x}\:\frac{{dw}}{{dx}}\:\:=\:\frac{{w}−{w}^{\mathrm{2}} }{\mathrm{1}+{w}}\:−\:{w}\:=\:\frac{−\mathrm{2}{w}^{\mathrm{2}} }{\mathrm{1}+{w}} \\ $$$$\frac{\left(\mathrm{1}+{w}\right)\:{dw}}{{w}^{\mathrm{2}} }\:=\:−\mathrm{2}\:\frac{{dx}}{{x}} \\ $$$$\int\:\left({w}^{−\mathrm{2}} +{w}^{−\mathrm{1}} \right){dw}\:=\:−\mathrm{2}\int\:\frac{{dx}}{{x}} \\ $$$$−\frac{\mathrm{1}}{{w}}\:+\:\mathrm{ln}\:\mid{w}\mid\:=\:−\mathrm{2}\:\mathrm{ln}\:\mid{x}\mid\:+\:\mathrm{c} \\ $$$$\mathrm{ln}\:\mid\:\frac{{w}}{{x}^{\mathrm{2}} }\mid\:=\:\frac{\mathrm{1}}{{w}}\:+\:{c}\: \\ $$$$\frac{{y}}{{x}^{\mathrm{3}} \:}\:=\:{e}^{\frac{\mathrm{1}}{{x}}\:+\:{c}} \Leftrightarrow\:\mathrm{y}\:=\:{x}^{\mathrm{3}} \:\left({Ce}^{\frac{\mathrm{1}}{{x}}} \right) \\ $$
