Question Number 98823 by john santu last updated on 16/Jun/20

Commented by bramlex last updated on 16/Jun/20
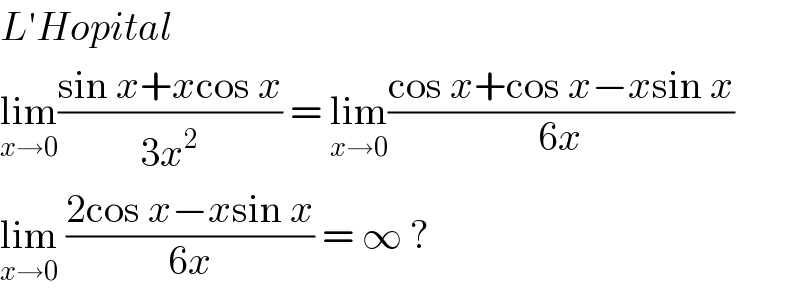
$${L}'{Hopital}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}+{x}\mathrm{cos}\:{x}}{\mathrm{3}{x}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:{x}+\mathrm{cos}\:{x}−{x}\mathrm{sin}\:{x}}{\mathrm{6}{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:{x}−{x}\mathrm{sin}\:{x}}{\mathrm{6}{x}}\:=\:\infty\:?\: \\ $$
Commented by bemath last updated on 16/Jun/20
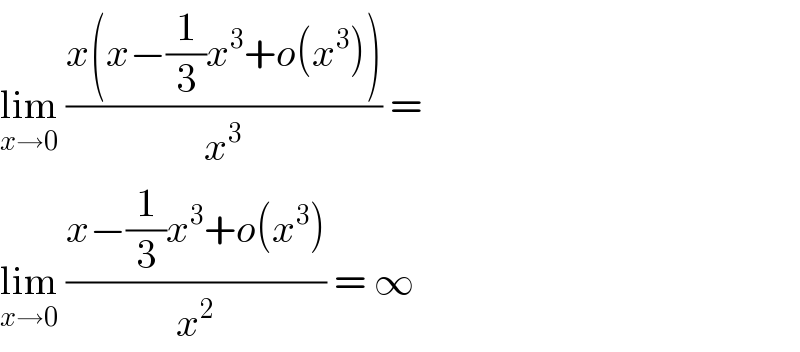
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left({x}−\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} +{o}\left({x}^{\mathrm{3}} \right)\right)}{{x}^{\mathrm{3}} }\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}−\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} +{o}\left({x}^{\mathrm{3}} \right)}{{x}^{\mathrm{2}} }\:=\:\infty \\ $$
