Menu Close

Question-98859

Tinku Tara 0 Comments
Pin




Question Number 98859 by peter frank last updated on 16/Jun/20
Commented by mr W last updated on 16/Jun/20
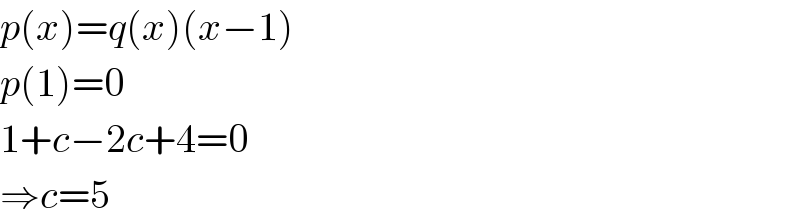
p(x)=q(x)(x−1) p(1)=0 1+c−2c+4=0 ⇒c=5
$${p}\left({x}\right)={q}\left({x}\right)\left({x}−\mathrm{1}\right) \\ $$$${p}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{1}+{c}−\mathrm{2}{c}+\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{c}=\mathrm{5} \\ $$
Answered by Rasheed.Sindhi last updated on 16/Jun/20
(((1)),1,( c),(−2c),( 4)),(,,( 1),( c+1),(−c+1)),(,1,(c+1),(−c+1),(−c+5)) ) −c+5=0⇒c=5
$$\begin{pmatrix}{\left.\mathrm{1}\right)}&{\mathrm{1}}&{\:\:\:{c}}&{−\mathrm{2}{c}}&{\:\:\:\:\:\mathrm{4}}\\{}&{}&{\:\:\:\mathrm{1}}&{\:\:{c}+\mathrm{1}}&{−{c}+\mathrm{1}}\\{}&{\mathrm{1}}&{{c}+\mathrm{1}}&{−{c}+\mathrm{1}}&{−{c}+\mathrm{5}}\end{pmatrix}\:\: \\ $$$$−{c}+\mathrm{5}=\mathrm{0}\Rightarrow{c}=\mathrm{5} \\ $$
Commented by Rio Michael last updated on 17/Jun/20
please i will love to study this method of yours.. please hint me on how to use it.
$$\mathrm{please}\:\mathrm{i}\:\mathrm{will}\:\mathrm{love}\:\mathrm{to}\:\mathrm{study}\:\mathrm{this}\:\mathrm{method}\:\mathrm{of} \\ $$$$\mathrm{yours}..\:\mathrm{please}\:\mathrm{hint}\:\mathrm{me}\:\mathrm{on}\:\mathrm{how}\:\mathrm{to}\:\mathrm{use}\:\mathrm{it}. \\ $$
Commented by Rasheed.Sindhi last updated on 17/Jun/20
Let a polynomial P(x) is divided by x−r (Synthetically). 1. Write P(x) in descending order including missing terms with coefficients 0. For example if P(x)=3x^2 −8+4x^3 then P(x)=4x^3 +3x^2 +0x−8 2.The divisor should be of type x−r. r is called multiplyer In x−3,the multiplyer 3 and in x+3=x−(−3) the multiplyer is −3. 3.First row consist of multiplyer,separator & coefficients of p(x) Process Example. (C_0 x^3 +C_1 x^2 +C_2 x+C_3 )÷(x−r) (1),...,(7) are entries processed in order. (((r)),( C_0 ),C_1 ,C_2 ,C_3 ),(,,( (2)),((4)),((6))),(,( (1)),( (3)),((5)),((7))) ) (1)=C_0 (2)=(1).r=C_0 .r (3)=C_1 +(2) (4)=(3).r (5)=C_2 +(4) (6)=(5).r (7)=C_3 +(6)=remainder (1)x^2 +(3)x+(5)=quotient
$${Let}\:{a}\:{polynomial}\:{P}\left({x}\right)\:{is}\:{divided} \\ $$$${by}\:{x}−{r}\:\left({Synthetically}\right). \\ $$$$\mathrm{1}.\:{Write}\:{P}\left({x}\right)\:{in}\:{descending}\:{order} \\ $$$${including}\:{missing}\:{terms}\:{with} \\ $$$${coefficients}\:\mathrm{0}.\:{For}\:{example} \\ $$$${if}\:{P}\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{8}+\mathrm{4}{x}^{\mathrm{3}} \\ $$$$\:{then}\:\:\:\:{P}\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{0}{x}−\mathrm{8} \\ $$$$\mathrm{2}.{The}\:{divisor}\:{should}\:{be}\:{of}\:{type} \\ $$$${x}−{r}.\:{r}\:{is}\:{called}\:{multiplyer} \\ $$$${In}\:{x}−\mathrm{3},{the}\:{multiplyer}\:\mathrm{3}\:{and} \\ $$$${in}\:{x}+\mathrm{3}={x}−\left(−\mathrm{3}\right)\:{the}\:{multiplyer} \\ $$$${is}\:−\mathrm{3}. \\ $$$$\mathrm{3}.{First}\:{row}\:{consist}\:{of} \\ $$$${multiplyer},{separator}\:\&\:{coefficients}\:{of}\:{p}\left({x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Process} \\ $$$$\mathcal{E}{xample}. \\ $$$$\left({C}_{\mathrm{0}} {x}^{\mathrm{3}} +{C}_{\mathrm{1}} {x}^{\mathrm{2}} +{C}_{\mathrm{2}} {x}+{C}_{\mathrm{3}} \right)\boldsymbol{\div}\left({x}−{r}\right) \\ $$$$\left(\mathrm{1}\right),…,\left(\mathrm{7}\right)\:{are}\:{entries}\:{processed}\:{in}\:{order}. \\ $$$$\begin{pmatrix}{\left.{r}\right)}&{\:\:\:\:{C}_{\mathrm{0}} }&{{C}_{\mathrm{1}} }&{{C}_{\mathrm{2}} }&{{C}_{\mathrm{3}} }\\{}&{}&{\:\left(\mathrm{2}\right)}&{\left(\mathrm{4}\right)}&{\left(\mathrm{6}\right)}\\{}&{\:\left(\mathrm{1}\right)}&{\:\left(\mathrm{3}\right)}&{\left(\mathrm{5}\right)}&{\left(\mathrm{7}\right)}\end{pmatrix} \\ $$$$\left(\mathrm{1}\right)={C}_{\mathrm{0}} \\ $$$$\left(\mathrm{2}\right)=\left(\mathrm{1}\right).{r}={C}_{\mathrm{0}} .{r} \\ $$$$\left(\mathrm{3}\right)={C}_{\mathrm{1}} +\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{4}\right)=\left(\mathrm{3}\right).{r} \\ $$$$\left(\mathrm{5}\right)={C}_{\mathrm{2}} +\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{6}\right)=\left(\mathrm{5}\right).{r} \\ $$$$\left(\mathrm{7}\right)={C}_{\mathrm{3}} +\left(\mathrm{6}\right)={remainder} \\ $$$$\left(\mathrm{1}\right){x}^{\mathrm{2}} +\left(\mathrm{3}\right){x}+\left(\mathrm{5}\right)={quotient} \\ $$
Commented by Rio Michael last updated on 17/Jun/20
wow, nice method sir..thanks thanks alot sir.
$$\mathrm{wow},\:\mathrm{nice}\:\mathrm{method}\:\mathrm{sir}..\mathrm{thanks} \\ $$$$\mathrm{thanks}\:\mathrm{alot}\:\mathrm{sir}. \\ $$
Commented by bemath last updated on 18/Jun/20
Horner method sir
$$\mathrm{Horner}\:\mathrm{method}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 16/Jun/20
p(x) =x^3 −1 +cx^2 −c −2c(x−1)−2c +4 +1+c =(x−1)(x^2 +x+1)+c(x−1)(x+1) −2c(x−1) +5−c =(x−1){x^2 +x+1 +cx−c) +5−c x−1 divide p(x) ⇒5−c =0 ⇒c=5 and p(x)=(x−1)Q(x) with Q(x)=x^2 +6x−4
$$\mathrm{p}\left(\mathrm{x}\right)\:=\mathrm{x}^{\mathrm{3}} −\mathrm{1}\:+\mathrm{cx}^{\mathrm{2}} −\mathrm{c}\:−\mathrm{2c}\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{2c}\:+\mathrm{4}\:+\mathrm{1}+\mathrm{c} \\ $$$$=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+\mathrm{c}\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)\:−\mathrm{2c}\left(\mathrm{x}−\mathrm{1}\right)\:+\mathrm{5}−\mathrm{c} \\ $$$$=\left(\mathrm{x}−\mathrm{1}\right)\left\{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\:+\mathrm{cx}−\mathrm{c}\right)\:+\mathrm{5}−\mathrm{c} \\ $$$$\mathrm{x}−\mathrm{1}\:\mathrm{divide}\:\mathrm{p}\left(\mathrm{x}\right)\:\Rightarrow\mathrm{5}−\mathrm{c}\:=\mathrm{0}\:\Rightarrow\mathrm{c}=\mathrm{5}\:\mathrm{and}\:\mathrm{p}\left(\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{1}\right)\mathrm{Q}\left(\mathrm{x}\right)\:\mathrm{with} \\ $$$$\mathrm{Q}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{6x}−\mathrm{4} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *