Question-99123

Question Number 99123 by Mr.D.N. last updated on 18/Jun/20

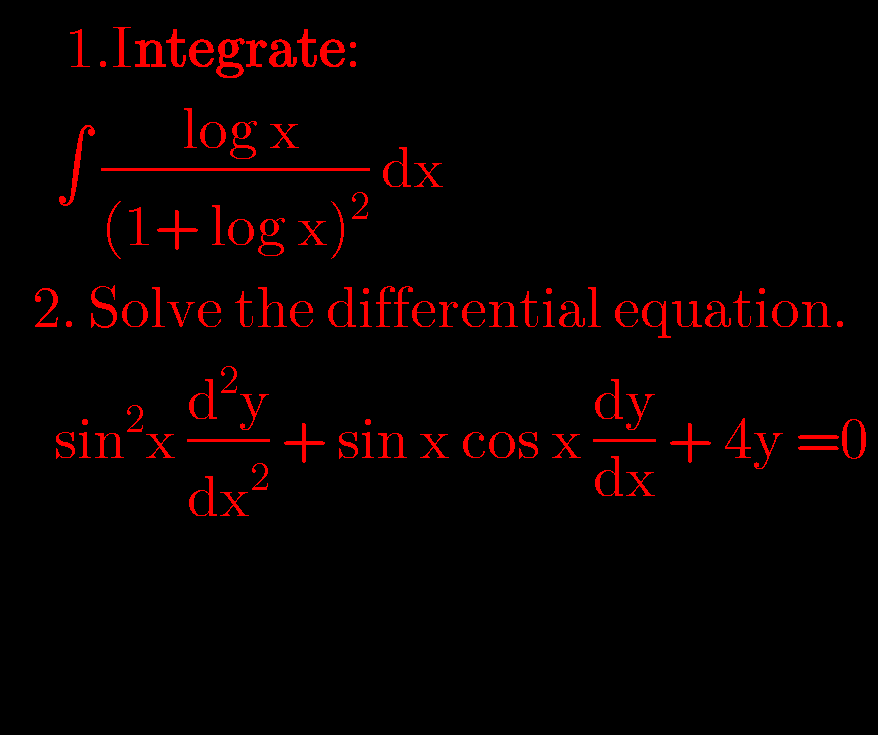
Commented by Rasheed.Sindhi last updated on 18/Jun/20

$${It}\:{seems}\:{that}\:{you}'{re}\:{experimenting} \\ $$$${about}\:{colour}\:{schemes}.\:{If}\:{you} \\ $$$${allow}\:{me}\:{to}\:{express}\:{my}\:{personal} \\ $$$${openion}\:{then}\:{I}\:{say}\:{that}\:{red}\:{text} \\ $$$${on}\:{black}\:{background}\:{is}\:{not}\:{so}\: \\ $$$${good}\:{for}\:{my}\:{eyes}! \\ $$

Answered by som(math1967) last updated on 18/Jun/20

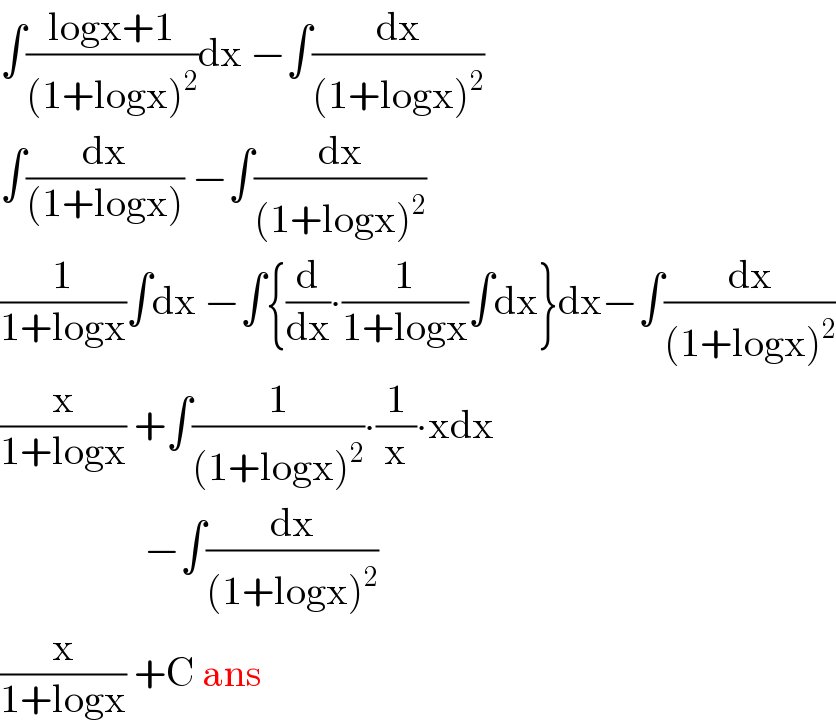
∫((logx+1)/((1+logx)^2 ))dx −∫(dx/((1+logx)^2 )) ∫(dx/((1+logx))) −∫(dx/((1+logx)^2 )) (1/(1+logx))∫dx −∫{(d/dx)∙(1/(1+logx))∫dx}dx−∫(dx/((1+logx)^2 )) (x/(1+logx)) +∫(1/((1+logx)^2 ))∙(1/x)∙xdx −∫(dx/((1+logx)^2 )) (x/(1+logx)) +C ans

$$\int\frac{\mathrm{logx}+\mathrm{1}}{\left(\mathrm{1}+\mathrm{logx}\right)^{\mathrm{2}} }\mathrm{dx}\:−\int\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{logx}\right)^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{logx}\right)}\:−\int\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{logx}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{logx}}\int\mathrm{dx}\:−\int\left\{\frac{\mathrm{d}}{\mathrm{dx}}\centerdot\frac{\mathrm{1}}{\mathrm{1}+\mathrm{logx}}\int\mathrm{dx}\right\}\mathrm{dx}−\int\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{logx}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{x}}{\mathrm{1}+\mathrm{logx}}\:+\int\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{logx}\right)^{\mathrm{2}} }\centerdot\frac{\mathrm{1}}{\mathrm{x}}\centerdot\mathrm{xdx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\int\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{logx}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{x}}{\mathrm{1}+\mathrm{logx}}\:+\mathrm{C}\:\mathrm{ans} \\ $$

Commented by Mr.D.N. last updated on 18/Jun/20

thanks mr.som you are greatest answering.

Answered by Dwaipayan Shikari last updated on 20/Jun/20

∫((logx)/((1+logx)^2 ))dx=∫(dx/((1+logx)))−∫(dx/((1+logx)^2 ))=∫((xdx)/(x(1+logx)))−∫((xdx)/(x(1+logx)^2 )) suppose[](1+logx)=t so,(1/x)=(dt/dx) And[]x=e^(t−1) This[]is[]another[]form ∫((xdx)/(x(1+logx)))−∫((xdx)/(x(1+logx)^2 ))=∫e^(t−1) ((1/t)−(1/t^2 ))dt =(1/e)∫e^t ((1/t)−(1/t^2 ))dt =(1/e)e^t ((1/t))+Constant =(x/((1+logx)))+Constant

$$\int\frac{{logx}}{\left(\mathrm{1}+{logx}\right)^{\mathrm{2}} }{dx}=\int\frac{{dx}}{\left(\mathrm{1}+{logx}\right)}−\int\frac{{dx}}{\left(\mathrm{1}+{logx}\right)^{\mathrm{2}} }=\int\frac{{xdx}}{{x}\left(\mathrm{1}+{logx}\right)}−\int\frac{{xdx}}{{x}\left(\mathrm{1}+{logx}\right)^{\mathrm{2}} } \\ $$$${suppose}\left[\right]\left(\mathrm{1}+{logx}\right)={t} \\ $$$${so},\frac{\mathrm{1}}{{x}}=\frac{{dt}}{{dx}} \\ $$$${And}\left[\right]{x}={e}^{{t}−\mathrm{1}} \\ $$$${This}\left[\right]{is}\left[\right]{another}\left[\right]{form} \\ $$$$\int\frac{{xdx}}{{x}\left(\mathrm{1}+{logx}\right)}−\int\frac{{xdx}}{{x}\left(\mathrm{1}+{logx}\right)^{\mathrm{2}} }=\int{e}^{{t}−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){dt} \\ $$$$=\frac{\mathrm{1}}{{e}}\int{e}^{{t}} \left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){dt} \\ $$$$=\frac{\mathrm{1}}{{e}}{e}^{{t}} \left(\frac{\mathrm{1}}{{t}}\right)+{Constant} \\ $$$$=\frac{{x}}{\left(\mathrm{1}+{logx}\right)}+{Constant} \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply