Question Number 99159 by bemath last updated on 19/Jun/20

Commented by som(math1967) last updated on 19/Jun/20
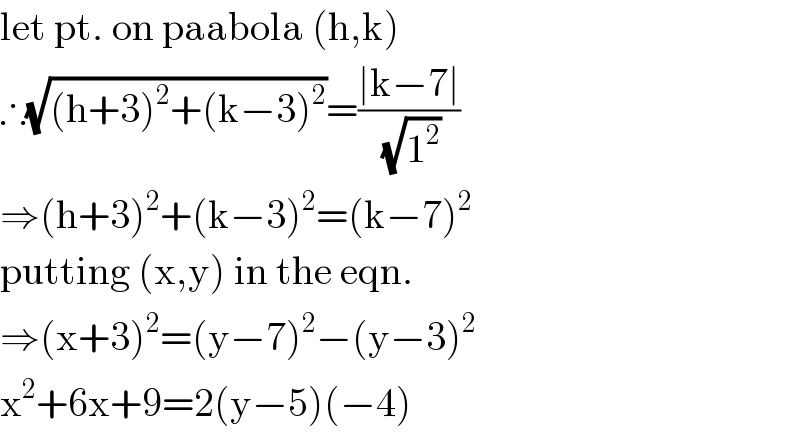
$$\mathrm{let}\:\mathrm{pt}.\:\mathrm{on}\:\mathrm{paabola}\:\left(\mathrm{h},\mathrm{k}\right) \\ $$$$\therefore\sqrt{\left(\mathrm{h}+\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{k}−\mathrm{3}\right)^{\mathrm{2}} }=\frac{\mid\mathrm{k}−\mathrm{7}\mid}{\:\sqrt{\mathrm{1}^{\mathrm{2}} }} \\ $$$$\Rightarrow\left(\mathrm{h}+\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{k}−\mathrm{3}\right)^{\mathrm{2}} =\left(\mathrm{k}−\mathrm{7}\right)^{\mathrm{2}} \\ $$$$\mathrm{putting}\:\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{in}\:\mathrm{the}\:\mathrm{eqn}. \\ $$$$\Rightarrow\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} =\left(\mathrm{y}−\mathrm{7}\right)^{\mathrm{2}} −\left(\mathrm{y}−\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{9}=\mathrm{2}\left(\mathrm{y}−\mathrm{5}\right)\left(−\mathrm{4}\right) \\ $$
Commented by bemath last updated on 19/Jun/20
$$\mathrm{yes}.\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
