Question-99205

Question Number 99205 by bemath last updated on 19/Jun/20

Commented by bramlex last updated on 19/Jun/20

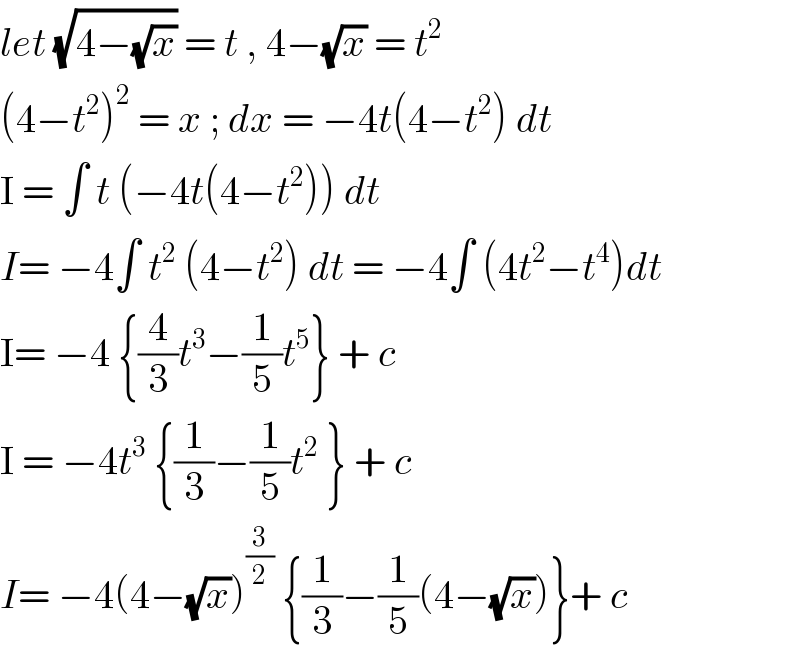
let (√(4−(√x))) = t , 4−(√x) = t^2 (4−t^2 )^2 = x ; dx = −4t(4−t^2 ) dt I = ∫ t (−4t(4−t^2 )) dt I= −4∫ t^2 (4−t^2 ) dt = −4∫ (4t^2 −t^4 )dt I= −4 {(4/3)t^3 −(1/5)t^5 } + c I = −4t^3 {(1/3)−(1/5)t^2 } + c I= −4(4−(√x))^(3/2) {(1/3)−(1/5)(4−(√x))}+ c

$${let}\:\sqrt{\mathrm{4}−\sqrt{{x}}}\:=\:{t}\:,\:\mathrm{4}−\sqrt{{x}}\:=\:{t}^{\mathrm{2}} \\ $$$$\left(\mathrm{4}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} \:=\:{x}\:;\:{dx}\:=\:−\mathrm{4}{t}\left(\mathrm{4}−{t}^{\mathrm{2}} \right)\:{dt}\: \\ $$$$\mathrm{I}\:=\:\int\:{t}\:\left(−\mathrm{4}{t}\left(\mathrm{4}−{t}^{\mathrm{2}} \right)\right)\:{dt}\: \\ $$$${I}=\:−\mathrm{4}\int\:{t}^{\mathrm{2}} \:\left(\mathrm{4}−{t}^{\mathrm{2}} \right)\:{dt}\:=\:−\mathrm{4}\int\:\left(\mathrm{4}{t}^{\mathrm{2}} −{t}^{\mathrm{4}} \right){dt} \\ $$$$\mathrm{I}=\:−\mathrm{4}\:\left\{\frac{\mathrm{4}}{\mathrm{3}}{t}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{5}}{t}^{\mathrm{5}} \right\}\:+\:{c} \\ $$$$\mathrm{I}\:=\:−\mathrm{4}{t}^{\mathrm{3}} \:\left\{\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}{t}^{\mathrm{2}} \:\right\}\:+\:{c}\: \\ $$$${I}=\:−\mathrm{4}\left(\mathrm{4}−\sqrt{{x}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\left\{\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{4}−\sqrt{{x}}\right)\right\}+\:{c} \\ $$

Answered by mathmax by abdo last updated on 19/Jun/20

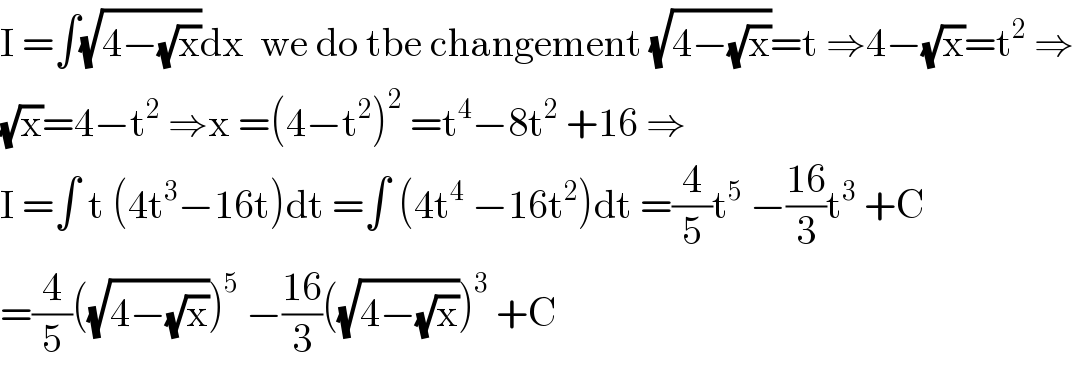
I =∫(√(4−(√x)))dx we do tbe changement (√(4−(√x)))=t ⇒4−(√x)=t^2 ⇒ (√x)=4−t^2 ⇒x =(4−t^2 )^2 =t^4 −8t^2 +16 ⇒ I =∫ t (4t^3 −16t)dt =∫ (4t^4 −16t^2 )dt =(4/5)t^5 −((16)/3)t^3 +C =(4/5)((√(4−(√x))))^5 −((16)/3)((√(4−(√x))))^3 +C

$$\mathrm{I}\:=\int\sqrt{\mathrm{4}−\sqrt{\mathrm{x}}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{changement}\:\sqrt{\mathrm{4}−\sqrt{\mathrm{x}}}=\mathrm{t}\:\Rightarrow\mathrm{4}−\sqrt{\mathrm{x}}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\sqrt{\mathrm{x}}=\mathrm{4}−\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}\:=\left(\mathrm{4}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} \:=\mathrm{t}^{\mathrm{4}} −\mathrm{8t}^{\mathrm{2}} \:+\mathrm{16}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\mathrm{t}\:\left(\mathrm{4t}^{\mathrm{3}} −\mathrm{16t}\right)\mathrm{dt}\:=\int\:\left(\mathrm{4t}^{\mathrm{4}} \:−\mathrm{16t}^{\mathrm{2}} \right)\mathrm{dt}\:=\frac{\mathrm{4}}{\mathrm{5}}\mathrm{t}^{\mathrm{5}} \:−\frac{\mathrm{16}}{\mathrm{3}}\mathrm{t}^{\mathrm{3}} \:+\mathrm{C} \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}\left(\sqrt{\mathrm{4}−\sqrt{\mathrm{x}}}\right)^{\mathrm{5}} \:−\frac{\mathrm{16}}{\mathrm{3}}\left(\sqrt{\mathrm{4}−\sqrt{\mathrm{x}}}\right)^{\mathrm{3}} \:+\mathrm{C} \\ $$

Commented by bemath last updated on 19/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$

Commented by mathmax by abdo last updated on 19/Jun/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Answered by MJS last updated on 19/Jun/20

∫(√(4−(√x)))dx= [t=(√(4−(√x))) → dx=−4(√x)(√(4−(√x)))dt] x=(t^2 −4)^2 ∧0≤t≤2 ⇔ 0≤x≤16 =4∫t^4 −4t^2 dt=(4/5)t^5 −((16)/3)t^3 = =(4/(15))(3x−4(√x)−32)(√(4−(√x))))+C

$$\int\sqrt{\mathrm{4}−\sqrt{{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{4}−\sqrt{{x}}}\:\rightarrow\:{dx}=−\mathrm{4}\sqrt{{x}}\sqrt{\mathrm{4}−\sqrt{{x}}}{dt}\right] \\ $$$$\:\:\:\:\:\:\:{x}=\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} \wedge\mathrm{0}\leqslant{t}\leqslant\mathrm{2}\:\Leftrightarrow\:\mathrm{0}\leqslant{x}\leqslant\mathrm{16} \\ $$$$=\mathrm{4}\int{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} {dt}=\frac{\mathrm{4}}{\mathrm{5}}{t}^{\mathrm{5}} −\frac{\mathrm{16}}{\mathrm{3}}{t}^{\mathrm{3}} = \\ $$$$\left.=\frac{\mathrm{4}}{\mathrm{15}}\left(\mathrm{3}{x}−\mathrm{4}\sqrt{{x}}−\mathrm{32}\right)\sqrt{\mathrm{4}−\sqrt{{x}}}\right)+{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply