Question-99218

Question Number 99218 by 9027201563 last updated on 19/Jun/20

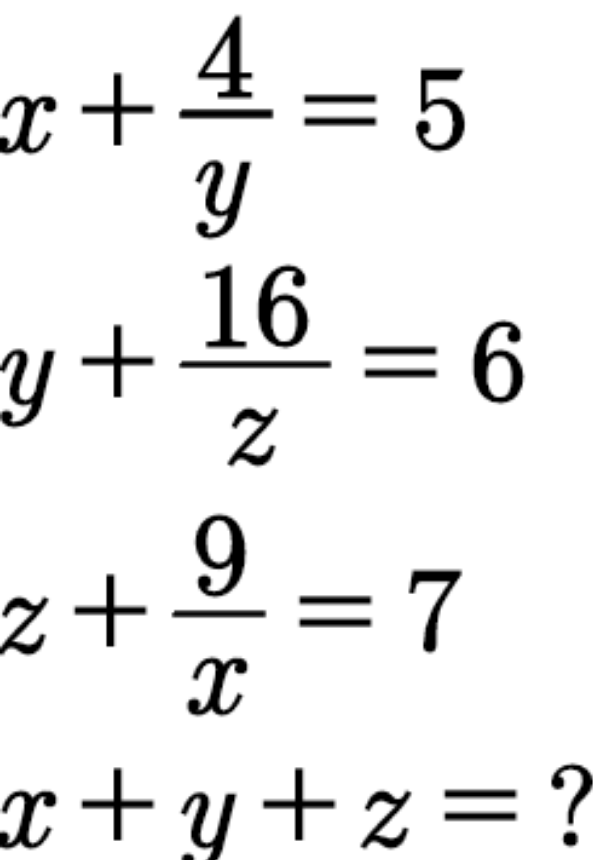
Commented by 9027201563 last updated on 19/Jun/20

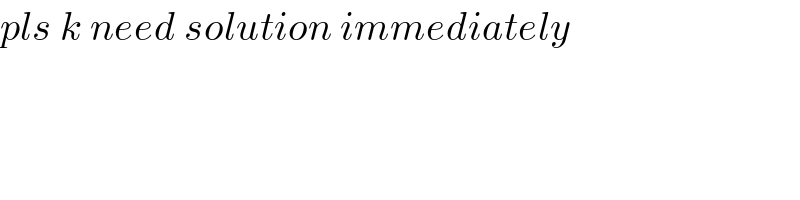
$${pls}\:{k}\:{need}\:{solution}\:{immediately} \\ $$

Commented by bobhans last updated on 19/Jun/20

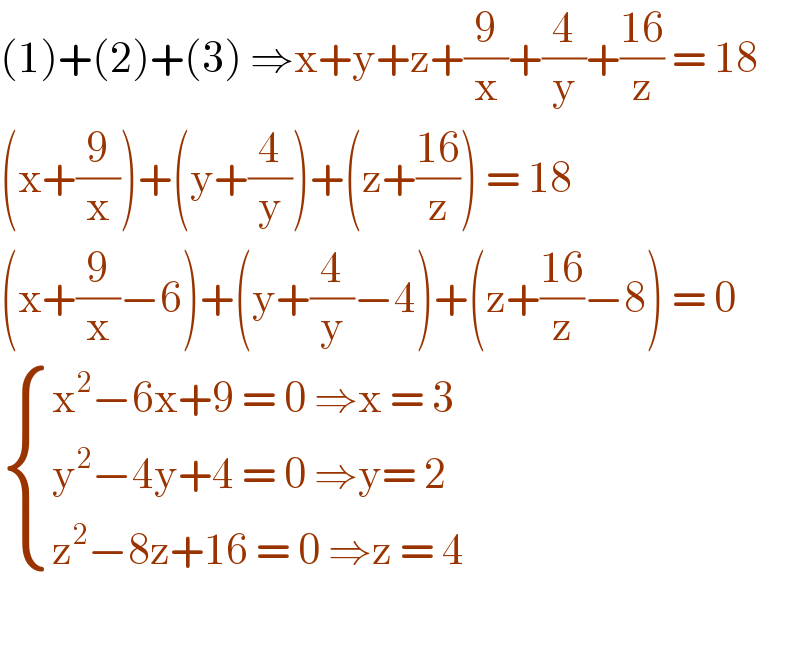
(1)+(2)+(3) ⇒x+y+z+(9/x)+(4/y)+((16)/z) = 18 (x+(9/x))+(y+(4/y))+(z+((16)/z)) = 18 (x+(9/x)−6)+(y+(4/y)−4)+(z+((16)/z)−8) = 0 { ((x^2 −6x+9 = 0 ⇒x = 3)),((y^2 −4y+4 = 0 ⇒y= 2)),((z^2 −8z+16 = 0 ⇒z = 4 )) :}

$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)+\left(\mathrm{3}\right)\:\Rightarrow\mathrm{x}+\mathrm{y}+\mathrm{z}+\frac{\mathrm{9}}{\mathrm{x}}+\frac{\mathrm{4}}{\mathrm{y}}+\frac{\mathrm{16}}{\mathrm{z}}\:=\:\mathrm{18} \\ $$$$\left(\mathrm{x}+\frac{\mathrm{9}}{\mathrm{x}}\right)+\left(\mathrm{y}+\frac{\mathrm{4}}{\mathrm{y}}\right)+\left(\mathrm{z}+\frac{\mathrm{16}}{\mathrm{z}}\right)\:=\:\mathrm{18} \\ $$$$\left(\mathrm{x}+\frac{\mathrm{9}}{\mathrm{x}}−\mathrm{6}\right)+\left(\mathrm{y}+\frac{\mathrm{4}}{\mathrm{y}}−\mathrm{4}\right)+\left(\mathrm{z}+\frac{\mathrm{16}}{\mathrm{z}}−\mathrm{8}\right)\:=\:\mathrm{0} \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{9}\:=\:\mathrm{0}\:\Rightarrow\mathrm{x}\:=\:\mathrm{3}}\\{\mathrm{y}^{\mathrm{2}} −\mathrm{4y}+\mathrm{4}\:=\:\mathrm{0}\:\Rightarrow\mathrm{y}=\:\mathrm{2}}\\{\mathrm{z}^{\mathrm{2}} −\mathrm{8z}+\mathrm{16}\:=\:\mathrm{0}\:\Rightarrow\mathrm{z}\:=\:\mathrm{4}\:}\end{cases} \\ $$$$ \\ $$

Commented by 9027201563 last updated on 19/Jun/20

Thanks Alot I really appreciate

Facebook Tweet Pin

Leave a Reply Cancel reply