Question-99259

Question Number 99259 by DGmichael last updated on 19/Jun/20

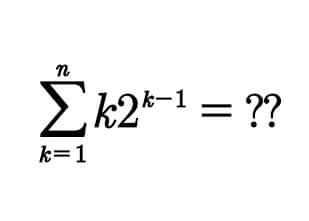
Answered by abdomathmax last updated on 19/Jun/20

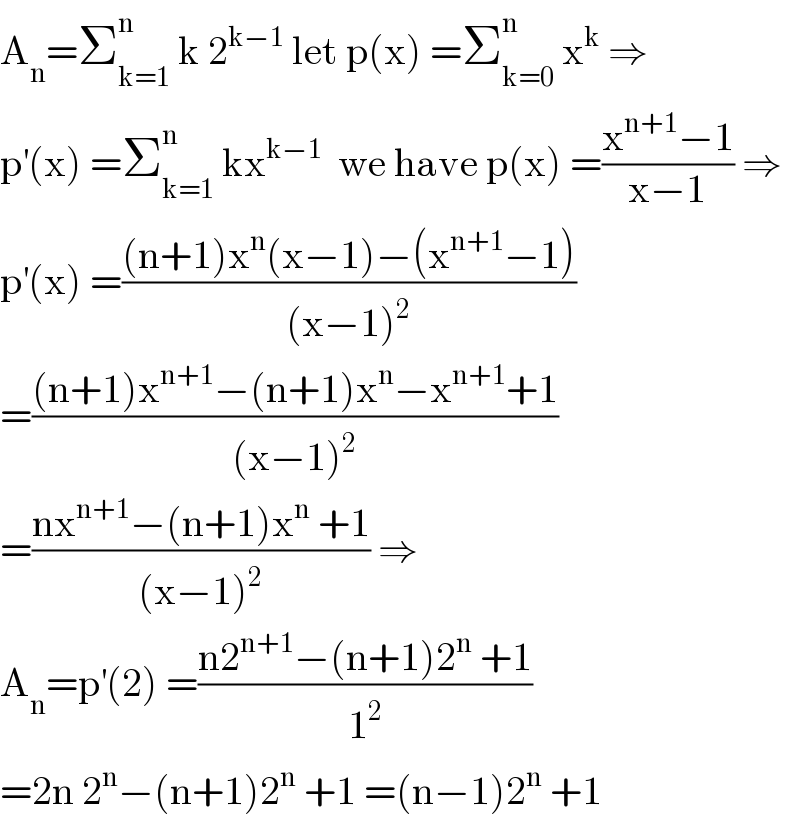
A_n =Σ_(k=1) ^n k 2^(k−1) let p(x) =Σ_(k=0) ^n x^k ⇒ p^′ (x) =Σ_(k=1) ^n kx^(k−1) we have p(x) =((x^(n+1) −1)/(x−1)) ⇒ p^′ (x) =(((n+1)x^n (x−1)−(x^(n+1) −1))/((x−1)^2 )) =(((n+1)x^(n+1) −(n+1)x^n −x^(n+1) +1)/((x−1)^2 )) =((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒ A_n =p^′ (2) =((n2^(n+1) −(n+1)2^n +1)/1^2 ) =2n 2^n −(n+1)2^n +1 =(n−1)2^n +1

$$\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}\:\mathrm{2}^{\mathrm{k}−\mathrm{1}} \:\mathrm{let}\:\mathrm{p}\left(\mathrm{x}\right)\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{x}^{\mathrm{k}} \:\Rightarrow \\ $$$$\mathrm{p}^{'} \left(\mathrm{x}\right)\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{kx}^{\mathrm{k}−\mathrm{1}} \:\:\mathrm{we}\:\mathrm{have}\:\mathrm{p}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{p}^{'} \left(\mathrm{x}\right)\:=\frac{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} \left(\mathrm{x}−\mathrm{1}\right)−\left(\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}\right)}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} −\mathrm{x}^{\mathrm{n}+\mathrm{1}} +\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$$$=\frac{\mathrm{nx}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} \:+\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\mathrm{p}^{'} \left(\mathrm{2}\right)\:=\frac{\mathrm{n2}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}} \:+\mathrm{1}}{\mathrm{1}^{\mathrm{2}} } \\ $$$$=\mathrm{2n}\:\mathrm{2}^{\mathrm{n}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}} \:+\mathrm{1}\:=\left(\mathrm{n}−\mathrm{1}\right)\mathrm{2}^{\mathrm{n}} \:+\mathrm{1} \\ $$

Commented by DGmichael last updated on 19/Jun/20

thanks sir !

Answered by mr W last updated on 19/Jun/20

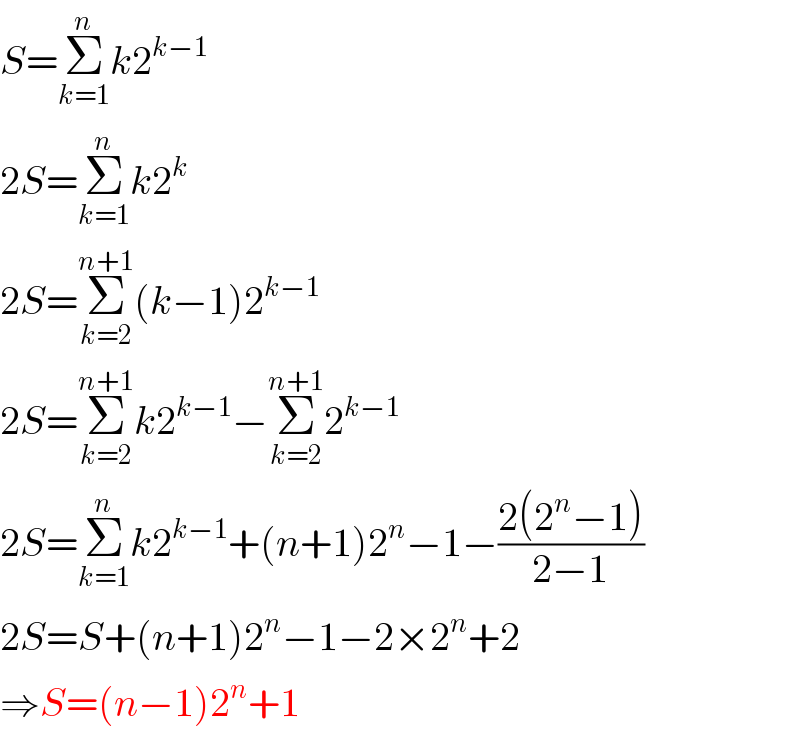
S=Σ_(k=1) ^n k2^(k−1) 2S=Σ_(k=1) ^n k2^k 2S=Σ_(k=2) ^(n+1) (k−1)2^(k−1) 2S=Σ_(k=2) ^(n+1) k2^(k−1) −Σ_(k=2) ^(n+1) 2^(k−1) 2S=Σ_(k=1) ^n k2^(k−1) +(n+1)2^n −1−((2(2^n −1))/(2−1)) 2S=S+(n+1)2^n −1−2×2^n +2 ⇒S=(n−1)2^n +1

$${S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}−\mathrm{1}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}\left({k}−\mathrm{1}\right)\mathrm{2}^{{k}−\mathrm{1}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{k}\mathrm{2}^{{k}−\mathrm{1}} −\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}\mathrm{2}^{{k}−\mathrm{1}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}−\mathrm{1}} +\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}} −\mathrm{1}−\frac{\mathrm{2}\left(\mathrm{2}^{{n}} −\mathrm{1}\right)}{\mathrm{2}−\mathrm{1}} \\ $$$$\mathrm{2}{S}={S}+\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}} −\mathrm{1}−\mathrm{2}×\mathrm{2}^{{n}} +\mathrm{2} \\ $$$$\Rightarrow{S}=\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}} +\mathrm{1} \\ $$

Commented by Ar Brandon last updated on 20/Jun/20

Cool, I erred��

Commented by DGmichael last updated on 20/Jun/20

��

Facebook Tweet Pin

Leave a Reply Cancel reply