Question Number 99286 by bobhans last updated on 20/Jun/20
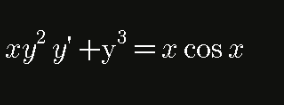
Commented by bemath last updated on 20/Jun/20

$$\mathrm{Bernoulli}\:\mathrm{equation}\: \\ $$
Commented by bemath last updated on 20/Jun/20
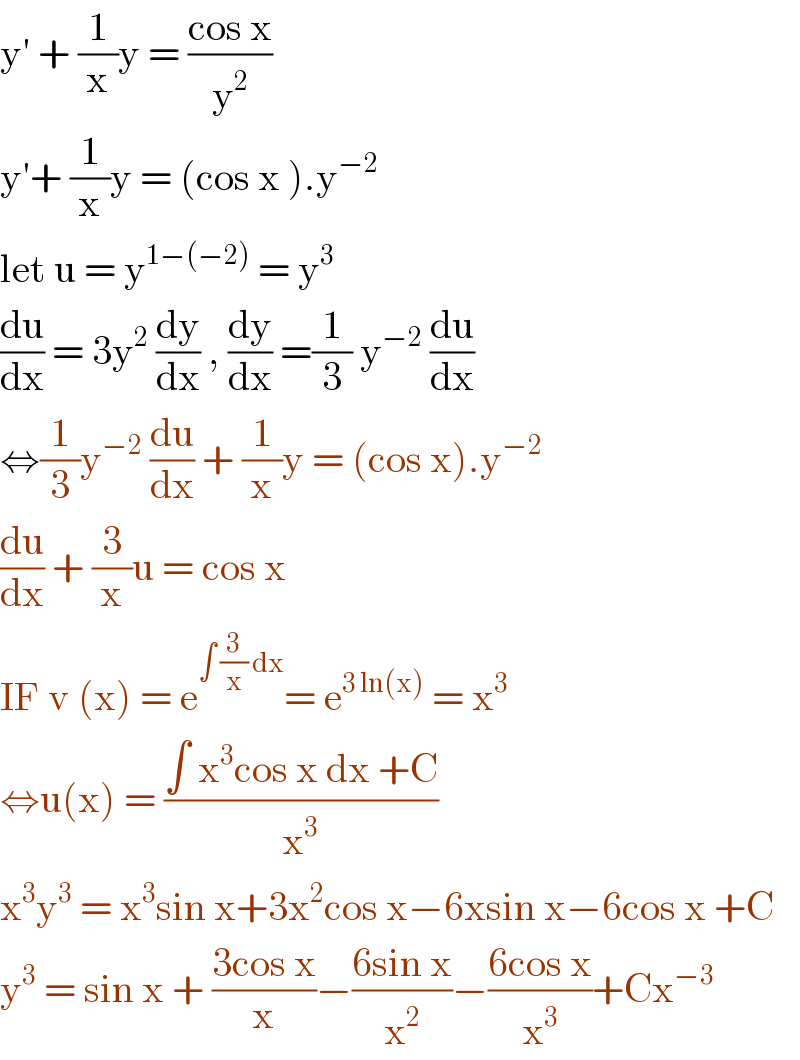
$$\mathrm{y}'\:+\:\frac{\mathrm{1}}{\mathrm{x}}\mathrm{y}\:=\:\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{y}^{\mathrm{2}} } \\ $$$$\mathrm{y}'+\:\frac{\mathrm{1}}{\mathrm{x}}\mathrm{y}\:=\:\left(\mathrm{cos}\:\mathrm{x}\:\right).\mathrm{y}^{−\mathrm{2}} \\ $$$$\mathrm{let}\:\mathrm{u}\:=\:\mathrm{y}^{\mathrm{1}−\left(−\mathrm{2}\right)} \:=\:\mathrm{y}^{\mathrm{3}} \: \\ $$$$\frac{\mathrm{du}}{\mathrm{dx}}\:=\:\mathrm{3y}^{\mathrm{2}} \:\frac{\mathrm{dy}}{\mathrm{dx}}\:,\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{y}^{−\mathrm{2}} \:\frac{\mathrm{du}}{\mathrm{dx}} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{3}}\mathrm{y}^{−\mathrm{2}} \:\frac{\mathrm{du}}{\mathrm{dx}}\:+\:\frac{\mathrm{1}}{\mathrm{x}}\mathrm{y}\:=\:\left(\mathrm{cos}\:\mathrm{x}\right).\mathrm{y}^{−\mathrm{2}} \\ $$$$\frac{\mathrm{du}}{\mathrm{dx}}\:+\:\frac{\mathrm{3}}{\mathrm{x}}\mathrm{u}\:=\:\mathrm{cos}\:\mathrm{x}\: \\ $$$$\mathrm{IF}\:\mathrm{v}\:\left(\mathrm{x}\right)\:=\:\mathrm{e}^{\int\:\frac{\mathrm{3}}{\mathrm{x}}\:\mathrm{dx}} =\:\mathrm{e}^{\mathrm{3}\:\mathrm{ln}\left(\mathrm{x}\right)} \:=\:\mathrm{x}^{\mathrm{3}} \\ $$$$\Leftrightarrow\mathrm{u}\left(\mathrm{x}\right)\:=\:\frac{\int\:\mathrm{x}^{\mathrm{3}} \mathrm{cos}\:\mathrm{x}\:\mathrm{dx}\:+\mathrm{C}}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\mathrm{x}^{\mathrm{3}} \mathrm{y}^{\mathrm{3}} \:=\:\mathrm{x}^{\mathrm{3}} \mathrm{sin}\:\mathrm{x}+\mathrm{3x}^{\mathrm{2}} \mathrm{cos}\:\mathrm{x}−\mathrm{6xsin}\:\mathrm{x}−\mathrm{6cos}\:\mathrm{x}\:+\mathrm{C} \\ $$$$\mathrm{y}^{\mathrm{3}} \:=\:\mathrm{sin}\:\mathrm{x}\:+\:\frac{\mathrm{3cos}\:\mathrm{x}}{\mathrm{x}}−\frac{\mathrm{6sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{6cos}\:\mathrm{x}}{\mathrm{x}^{\mathrm{3}} }+\mathrm{Cx}^{−\mathrm{3}} \\ $$
Commented by bobhans last updated on 20/Jun/20

$$\mathrm{great} \\ $$
