Question Number 99348 by bobhans last updated on 20/Jun/20

Commented by bemath last updated on 20/Jun/20
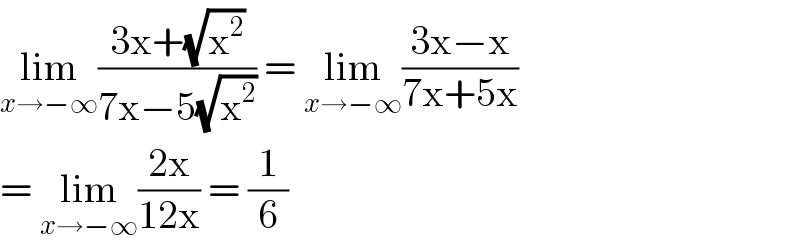
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\mathrm{3x}+\sqrt{\mathrm{x}^{\mathrm{2}} }}{\mathrm{7x}−\mathrm{5}\sqrt{\mathrm{x}^{\mathrm{2}} }}\:=\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\mathrm{3x}−\mathrm{x}}{\mathrm{7x}+\mathrm{5x}} \\ $$$$=\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\mathrm{2x}}{\mathrm{12x}}\:=\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Answered by abdomsup last updated on 20/Jun/20
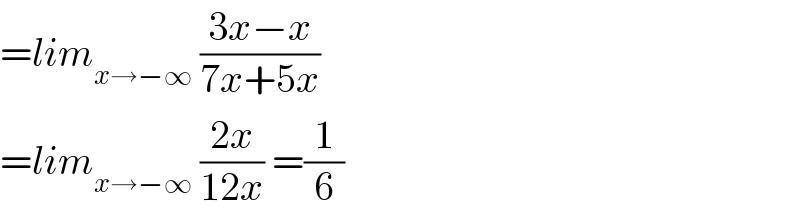
$$={lim}_{{x}\rightarrow−\infty} \:\frac{\mathrm{3}{x}−{x}}{\mathrm{7}{x}+\mathrm{5}{x}} \\ $$$$={lim}_{{x}\rightarrow−\infty} \:\frac{\mathrm{2}{x}}{\mathrm{12}{x}}\:=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
