Question Number 99392 by AwaisAhmed last updated on 20/Jun/20
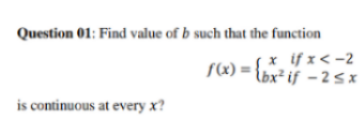
Commented by PRITHWISH SEN 2 last updated on 21/Jun/20
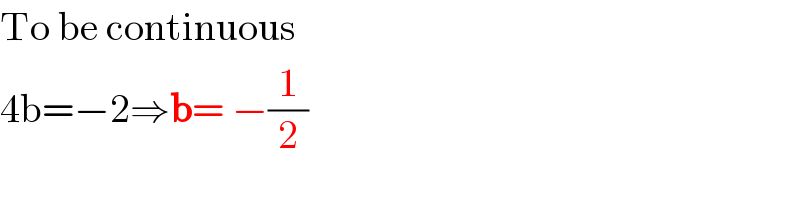
$$\mathrm{To}\:\mathrm{be}\:\mathrm{continuous}\: \\ $$$$\mathrm{4b}=−\mathrm{2}\Rightarrow\boldsymbol{\mathrm{b}}=\:−\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$
Answered by Rio Michael last updated on 20/Jun/20
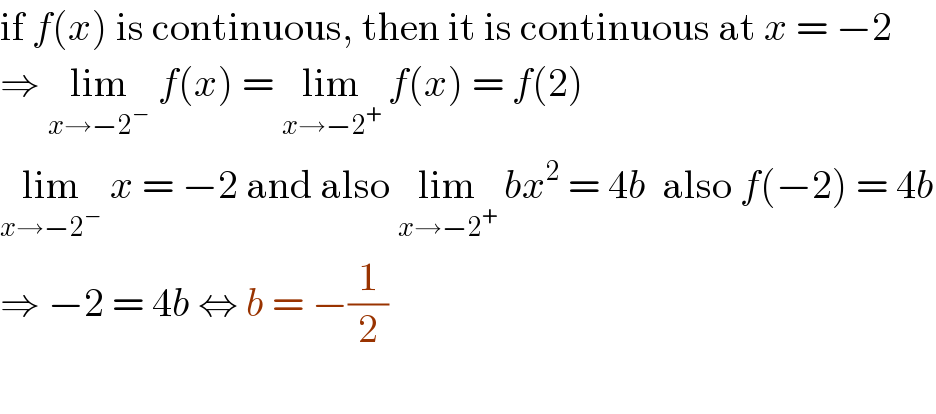
$$\mathrm{if}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{continuous},\:\mathrm{then}\:\mathrm{it}\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{at}\:{x}\:=\:−\mathrm{2} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow−\mathrm{2}^{−} } {\mathrm{lim}}\:{f}\left({x}\right)\:=\:\underset{{x}\rightarrow−\mathrm{2}^{+} } {\mathrm{lim}}\:{f}\left({x}\right)\:=\:{f}\left(\mathrm{2}\right) \\ $$$$\underset{{x}\rightarrow−\mathrm{2}^{−} } {\mathrm{lim}}\:{x}\:=\:−\mathrm{2}\:\mathrm{and}\:\mathrm{also}\:\underset{{x}\rightarrow−\mathrm{2}^{+} } {\mathrm{lim}}\:{bx}^{\mathrm{2}} \:=\:\mathrm{4}{b}\:\:\mathrm{also}\:{f}\left(−\mathrm{2}\right)\:=\:\mathrm{4}{b} \\ $$$$\Rightarrow\:−\mathrm{2}\:=\:\mathrm{4}{b}\:\Leftrightarrow\:{b}\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by PRITHWISH SEN 2 last updated on 21/Jun/20

$$\mathrm{sorry}\:\mathrm{itis}\:\mathrm{a}\:\mathrm{typo} \\ $$
