Menu Close

Question-99504

Tinku Tara 0 Comments
Pin




Question Number 99504 by pticantor last updated on 21/Jun/20
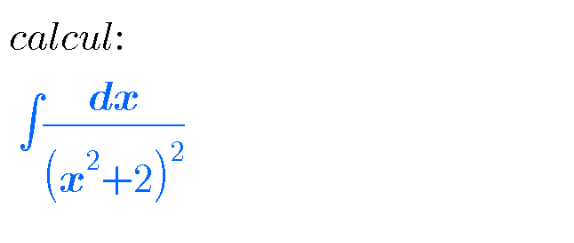
Answered by Ar Brandon last updated on 21/Jun/20
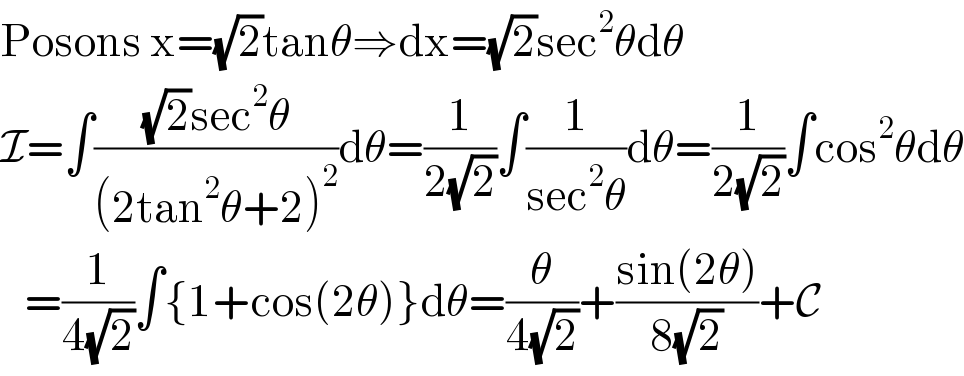
Posons x=(√2)tanθ⇒dx=(√2)sec^2 θdθ I=∫(((√2)sec^2 θ)/((2tan^2 θ+2)^2 ))dθ=(1/(2(√2)))∫(1/(sec^2 θ))dθ=(1/(2(√2)))∫cos^2 θdθ =(1/(4(√2)))∫{1+cos(2θ)}dθ=(θ/(4(√2)))+((sin(2θ))/(8(√2)))+C
$$\mathrm{Posons}\:\mathrm{x}=\sqrt{\mathrm{2}}\mathrm{tan}\theta\Rightarrow\mathrm{dx}=\sqrt{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\mathcal{I}=\int\frac{\sqrt{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} \theta}{\left(\mathrm{2tan}^{\mathrm{2}} \theta+\mathrm{2}\right)^{\mathrm{2}} }\mathrm{d}\theta=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{\mathrm{1}}{\mathrm{sec}^{\mathrm{2}} \theta}\mathrm{d}\theta=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\mathrm{cos}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\int\left\{\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)\right\}\mathrm{d}\theta=\frac{\theta}{\mathrm{4}\sqrt{\mathrm{2}}}+\frac{\mathrm{sin}\left(\mathrm{2}\theta\right)}{\mathrm{8}\sqrt{\mathrm{2}}}+\mathcal{C} \\ $$
Answered by Dwaipayan Shikari last updated on 21/Jun/20
Suppose,x=(√2)tanα so,(dx/dα)=(√2)sec^2 α ∫(((√2)sec^2 αdα)/(4(tan^2 α+1)^2 ))=(1/(2(√2)))∫cos^2 αdα=(1/(4(√2)))∫(1+cos2α)dα =(α/(4(√2)))+((sin2α)/(8(√2)))+constant =((tan^(−1) (x/( (√2))))/(4(√2)))+((sin(2tan^(−1) (x/( (√2)))))/(8(√2)))+constant
$${Suppose},{x}=\sqrt{\mathrm{2}}{tan}\alpha \\ $$$${so},\frac{{dx}}{{d}\alpha}=\sqrt{\mathrm{2}}{sec}^{\mathrm{2}} \alpha \\ $$$$\int\frac{\sqrt{\mathrm{2}}{sec}^{\mathrm{2}} \alpha{d}\alpha}{\mathrm{4}\left({tan}^{\mathrm{2}} \alpha+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int{cos}^{\mathrm{2}} \alpha{d}\alpha=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\int\left(\mathrm{1}+{cos}\mathrm{2}\alpha\right){d}\alpha \\ $$$$=\frac{\alpha}{\mathrm{4}\sqrt{\mathrm{2}}}+\frac{{sin}\mathrm{2}\alpha}{\mathrm{8}\sqrt{\mathrm{2}}}+{constant} \\ $$$$=\frac{\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{\mathrm{2}}}}{\mathrm{4}\sqrt{\mathrm{2}}}+\frac{{sin}\left(\mathrm{2tan}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{\mathrm{2}}}\right)}{\mathrm{8}\sqrt{\mathrm{2}}}+{constant} \\ $$
Answered by mathmax by abdo last updated on 21/Jun/20
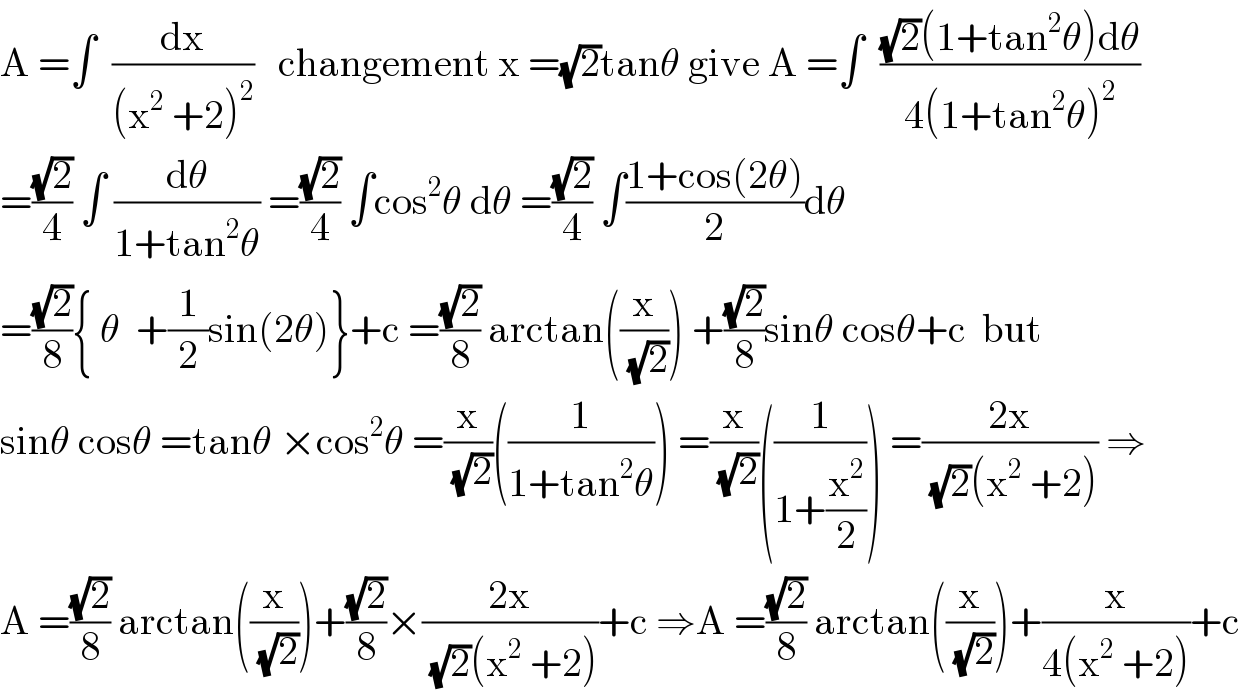
A =∫ (dx/((x^2 +2)^2 )) changement x =(√2)tanθ give A =∫ (((√2)(1+tan^2 θ)dθ)/(4(1+tan^2 θ)^2 )) =((√2)/4) ∫ (dθ/(1+tan^2 θ)) =((√2)/4) ∫cos^2 θ dθ =((√2)/4) ∫((1+cos(2θ))/2)dθ =((√2)/8){ θ +(1/2)sin(2θ)}+c =((√2)/8) arctan((x/( (√2)))) +((√2)/8)sinθ cosθ+c but sinθ cosθ =tanθ ×cos^2 θ =(x/( (√2)))((1/(1+tan^2 θ))) =(x/( (√2)))((1/(1+(x^2 /2)))) =((2x)/( (√2)(x^2 +2))) ⇒ A =((√2)/8) arctan((x/( (√2))))+((√2)/8)×((2x)/( (√2)(x^2 +2)))+c ⇒A =((√2)/8) arctan((x/( (√2))))+(x/(4(x^2 +2)))+c
$$\mathrm{A}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\right)^{\mathrm{2}} }\:\:\:\mathrm{changement}\:\mathrm{x}\:=\sqrt{\mathrm{2}}\mathrm{tan}\theta\:\mathrm{give}\:\mathrm{A}\:=\int\:\:\frac{\sqrt{\mathrm{2}}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)\mathrm{d}\theta}{\mathrm{4}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} } \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\int\:\frac{\mathrm{d}\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\int\mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{d}\theta\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\int\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\mathrm{d}\theta \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\left\{\:\theta\:\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\theta\right)\right\}+\mathrm{c}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\mathrm{arctan}\left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{sin}\theta\:\mathrm{cos}\theta+\mathrm{c}\:\:\mathrm{but} \\ $$$$\mathrm{sin}\theta\:\mathrm{cos}\theta\:=\mathrm{tan}\theta\:×\mathrm{cos}^{\mathrm{2}} \theta\:=\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\right)\:=\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}}\right)\:=\frac{\mathrm{2x}}{\:\sqrt{\mathrm{2}}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\right)}\:\Rightarrow \\ $$$$\mathrm{A}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\mathrm{arctan}\left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}×\frac{\mathrm{2x}}{\:\sqrt{\mathrm{2}}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\right)}+\mathrm{c}\:\Rightarrow\mathrm{A}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\mathrm{arctan}\left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{x}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\right)}+\mathrm{c} \\ $$
Answered by maths mind last updated on 22/Jun/20
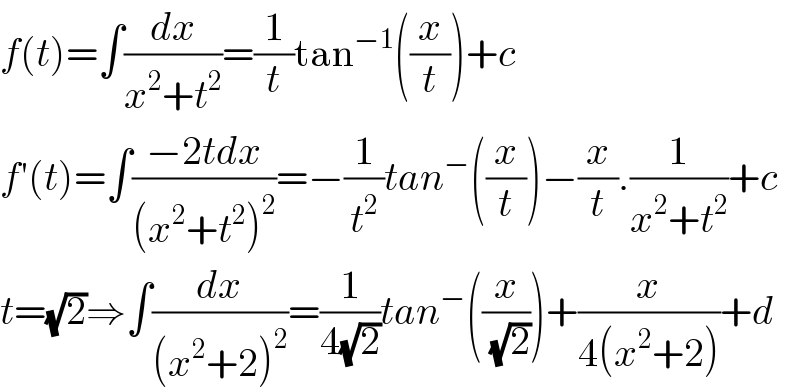
f(t)=∫(dx/(x^2 +t^2 ))=(1/t)tan^(−1) ((x/t))+c f′(t)=∫((−2tdx)/((x^2 +t^2 )^2 ))=−(1/t^2 )tan^− ((x/t))−(x/t).(1/(x^2 +t^2 ))+c t=(√2)⇒∫(dx/((x^2 +2)^2 ))=(1/(4(√2)))tan^− ((x/( (√2))))+(x/(4(x^2 +2)))+d
$${f}\left({t}\right)=\int\frac{{dx}}{{x}^{\mathrm{2}} +{t}^{\mathrm{2}} }=\frac{\mathrm{1}}{{t}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{{t}}\right)+{c} \\ $$$${f}'\left({t}\right)=\int\frac{−\mathrm{2}{tdx}}{\left({x}^{\mathrm{2}} +{t}^{\mathrm{2}} \right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{tan}^{−} \left(\frac{{x}}{{t}}\right)−\frac{{x}}{{t}}.\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{t}^{\mathrm{2}} }+{c} \\ $$$${t}=\sqrt{\mathrm{2}}\Rightarrow\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{tan}^{−} \left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)+\frac{{x}}{\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{2}\right)}+{d} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *