Question Number 99505 by bemath last updated on 21/Jun/20
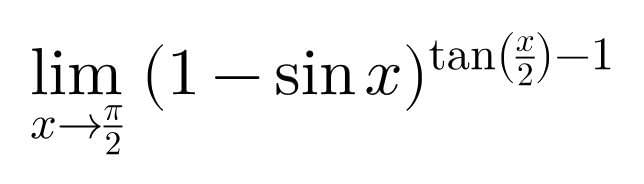
Commented by Dwaipayan Shikari last updated on 21/Jun/20

$${Ans}:\mathrm{1} \\ $$
Commented by Dwaipayan Shikari last updated on 21/Jun/20
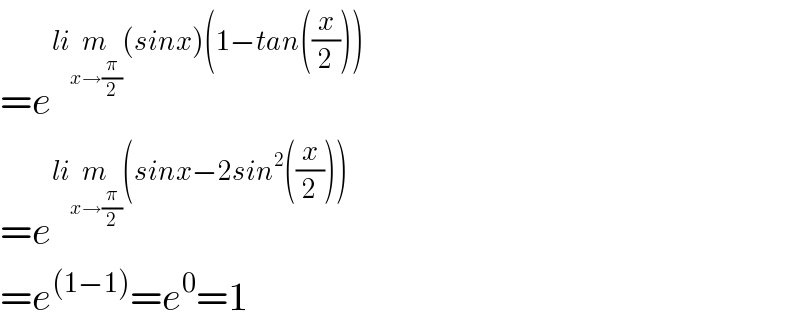
$$={e}^{{li}\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {{m}}\left({sinx}\right)\left(\mathrm{1}−{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)} \\ $$$$={e}^{{li}\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {{m}}\left({sinx}−\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)} \\ $$$$={e}^{\left(\mathrm{1}−\mathrm{1}\right)} ={e}^{\mathrm{0}} =\mathrm{1} \\ $$
Answered by john santu last updated on 22/Jun/20
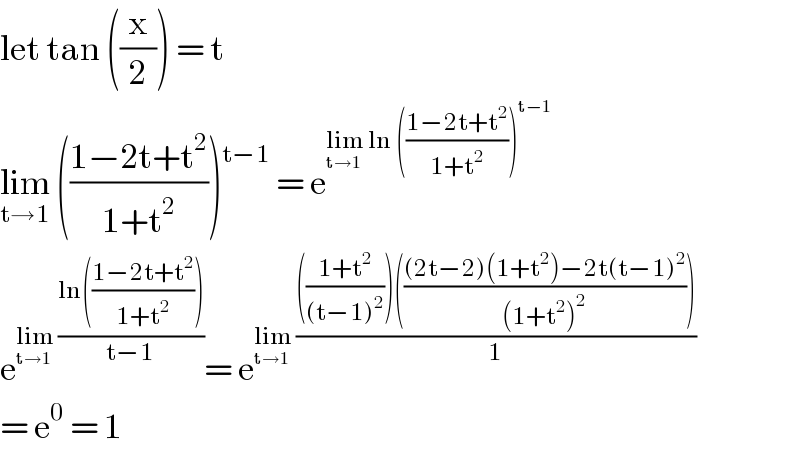
$$\mathrm{let}\:\mathrm{tan}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:=\:\mathrm{t} \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}−\mathrm{2t}+\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)\overset{\mathrm{t}−\mathrm{1}} {\:}\:=\:\mathrm{e}^{\underset{\mathrm{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\mathrm{ln}\:\left(\frac{\mathrm{1}−\mathrm{2t}+\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)^{\mathrm{t}−\mathrm{1}} } \\ $$$$\mathrm{e}^{\underset{\mathrm{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\frac{\mathrm{1}−\mathrm{2t}+\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)}{\mathrm{t}−\mathrm{1}}} =\:\mathrm{e}^{\underset{\mathrm{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }\right)\left(\frac{\left(\mathrm{2t}−\mathrm{2}\right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)−\mathrm{2t}\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\right)}{\mathrm{1}}} \\ $$$$=\:\mathrm{e}^{\mathrm{0}} \:=\:\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 21/Jun/20
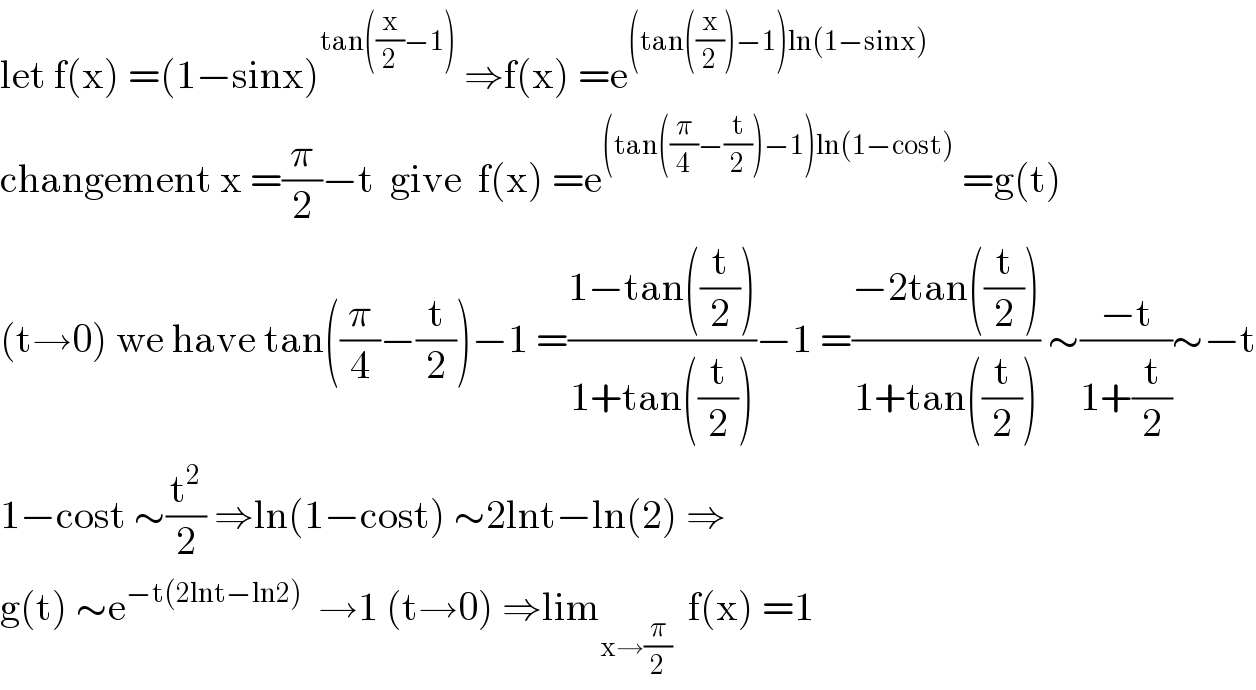
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\mathrm{1}−\mathrm{sinx}\right)^{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{1}\right)} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\left(\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{1}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{sinx}\right)} \\ $$$$\mathrm{changement}\:\mathrm{x}\:=\frac{\pi}{\mathrm{2}}−\mathrm{t}\:\:\mathrm{give}\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\left(\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{t}}{\mathrm{2}}\right)−\mathrm{1}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{cost}\right)} \:=\mathrm{g}\left(\mathrm{t}\right) \\ $$$$\left(\mathrm{t}\rightarrow\mathrm{0}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{t}}{\mathrm{2}}\right)−\mathrm{1}\:=\frac{\mathrm{1}−\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}−\mathrm{1}\:=\frac{−\mathrm{2tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}\:\sim\frac{−\mathrm{t}}{\mathrm{1}+\frac{\mathrm{t}}{\mathrm{2}}}\sim−\mathrm{t} \\ $$$$\mathrm{1}−\mathrm{cost}\:\sim\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{ln}\left(\mathrm{1}−\mathrm{cost}\right)\:\sim\mathrm{2lnt}−\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{t}\right)\:\sim\mathrm{e}^{−\mathrm{t}\left(\mathrm{2lnt}−\mathrm{ln2}\right)} \:\:\rightarrow\mathrm{1}\:\left(\mathrm{t}\rightarrow\mathrm{0}\right)\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{1} \\ $$
