Question Number 99562 by MamunSarker last updated on 21/Jun/20
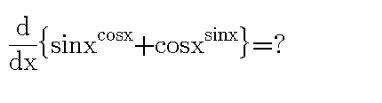
Answered by abdomathmax last updated on 21/Jun/20
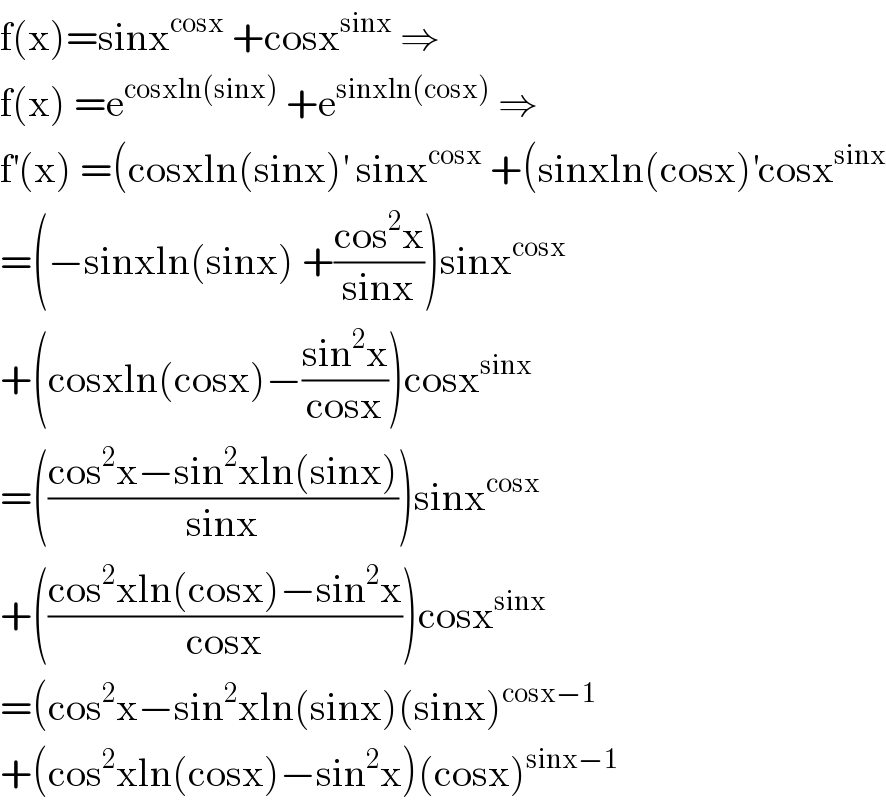
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{sinx}^{\mathrm{cosx}} \:+\mathrm{cosx}^{\mathrm{sinx}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\mathrm{cosxln}\left(\mathrm{sinx}\right)} \:+\mathrm{e}^{\mathrm{sinxln}\left(\mathrm{cosx}\right)} \:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\left(\mathrm{cosxln}\left(\mathrm{sinx}\right)^{'} \:\mathrm{sinx}^{\mathrm{cosx}} \:+\left(\mathrm{sinxln}\left(\mathrm{cosx}\right)^{'} \mathrm{cosx}^{\mathrm{sinx}} \right.\right. \\ $$$$=\left(−\mathrm{sinxln}\left(\mathrm{sinx}\right)\:+\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sinx}}\right)\mathrm{sinx}^{\mathrm{cosx}} \\ $$$$+\left(\mathrm{cosxln}\left(\mathrm{cosx}\right)−\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{cosx}}\right)\mathrm{cosx}^{\mathrm{sinx}} \\ $$$$=\left(\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{sin}^{\mathrm{2}} \mathrm{xln}\left(\mathrm{sinx}\right)}{\mathrm{sinx}}\right)\mathrm{sinx}^{\mathrm{cosx}} \\ $$$$+\left(\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{xln}\left(\mathrm{cosx}\right)−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{cosx}}\right)\mathrm{cosx}^{\mathrm{sinx}} \\ $$$$=\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{sin}^{\mathrm{2}} \mathrm{xln}\left(\mathrm{sinx}\right)\left(\mathrm{sinx}\right)^{\mathrm{cosx}−\mathrm{1}} \right. \\ $$$$+\left(\mathrm{cos}^{\mathrm{2}} \mathrm{xln}\left(\mathrm{cosx}\right)−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{cosx}\right)^{\mathrm{sinx}−\mathrm{1}} \\ $$
