Question Number 99655 by bemath last updated on 22/Jun/20

Commented by bramlex last updated on 22/Jun/20
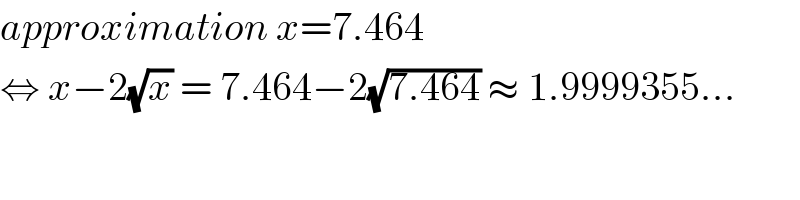
$${approximation}\:{x}=\mathrm{7}.\mathrm{464} \\ $$$$\Leftrightarrow\:{x}−\mathrm{2}\sqrt{{x}}\:=\:\mathrm{7}.\mathrm{464}−\mathrm{2}\sqrt{\mathrm{7}.\mathrm{464}}\:\approx\:\mathrm{1}.\mathrm{9999355}…\: \\ $$
Answered by Farruxjano last updated on 22/Jun/20
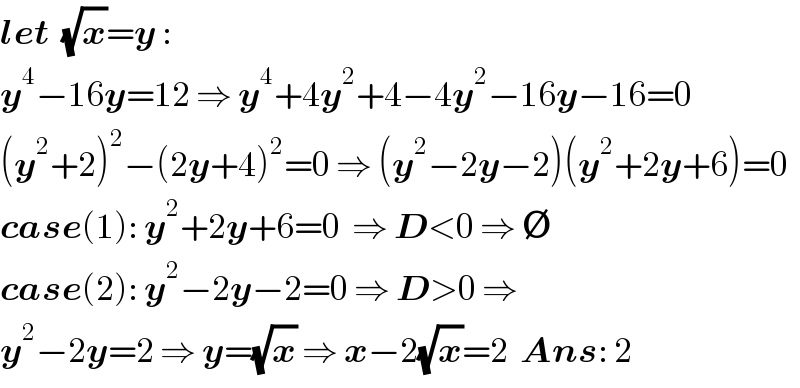
$$\boldsymbol{{let}}\:\:\sqrt{\boldsymbol{{x}}}=\boldsymbol{{y}}\:: \\ $$$$\boldsymbol{{y}}^{\mathrm{4}} −\mathrm{16}\boldsymbol{{y}}=\mathrm{12}\:\Rightarrow\:\boldsymbol{{y}}^{\mathrm{4}} +\mathrm{4}\boldsymbol{{y}}^{\mathrm{2}} +\mathrm{4}−\mathrm{4}\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{16}\boldsymbol{{y}}−\mathrm{16}=\mathrm{0} \\ $$$$\left(\boldsymbol{{y}}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} −\left(\mathrm{2}\boldsymbol{{y}}+\mathrm{4}\right)^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:\left(\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{y}}−\mathrm{2}\right)\left(\boldsymbol{{y}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{y}}+\mathrm{6}\right)=\mathrm{0} \\ $$$$\boldsymbol{{case}}\left(\mathrm{1}\right):\:\boldsymbol{{y}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{y}}+\mathrm{6}=\mathrm{0}\:\:\Rightarrow\:\boldsymbol{{D}}<\mathrm{0}\:\Rightarrow\:\boldsymbol{\varnothing} \\ $$$$\boldsymbol{{case}}\left(\mathrm{2}\right):\:\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{y}}−\mathrm{2}=\mathrm{0}\:\Rightarrow\:\boldsymbol{{D}}>\mathrm{0}\:\Rightarrow \\ $$$$\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{y}}=\mathrm{2}\:\Rightarrow\:\boldsymbol{{y}}=\sqrt{\boldsymbol{{x}}}\:\Rightarrow\:\boldsymbol{{x}}−\mathrm{2}\sqrt{\boldsymbol{{x}}}=\mathrm{2}\:\:\boldsymbol{{Ans}}:\:\mathrm{2} \\ $$
