Question Number 99761 by Lekhraj last updated on 23/Jun/20
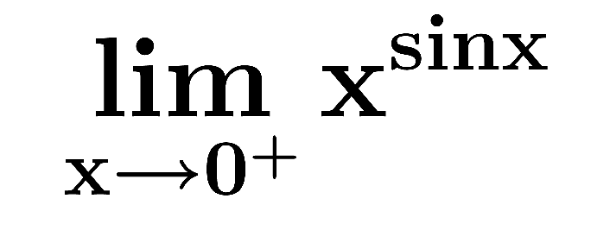
Commented by Dwaipayan Shikari last updated on 23/Jun/20

$${Ans}=\mathrm{1} \\ $$
Commented by Dwaipayan Shikari last updated on 23/Jun/20

$$={e}^{{li}\underset{{x}\rightarrow\mathrm{0}^{+} } {{m}}\left({x}−\mathrm{1}\right){sinx}} =\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 23/Jun/20
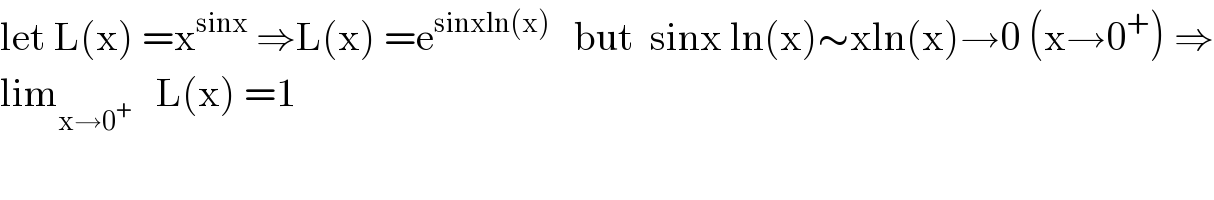
$$\mathrm{let}\:\mathrm{L}\left(\mathrm{x}\right)\:=\mathrm{x}^{\mathrm{sinx}} \:\Rightarrow\mathrm{L}\left(\mathrm{x}\right)\:=\mathrm{e}^{\mathrm{sinxln}\left(\mathrm{x}\right)} \:\:\:\mathrm{but}\:\:\mathrm{sinx}\:\mathrm{ln}\left(\mathrm{x}\right)\sim\mathrm{xln}\left(\mathrm{x}\right)\rightarrow\mathrm{0}\:\left(\mathrm{x}\rightarrow\mathrm{0}^{+} \right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\:\mathrm{L}\left(\mathrm{x}\right)\:=\mathrm{1} \\ $$
Commented by Lekhraj last updated on 23/Jun/20

$$\mathrm{Thanks}\:.\: \\ $$
