Question Number 99779 by john santu last updated on 23/Jun/20

Commented by Dwaipayan Shikari last updated on 23/Jun/20
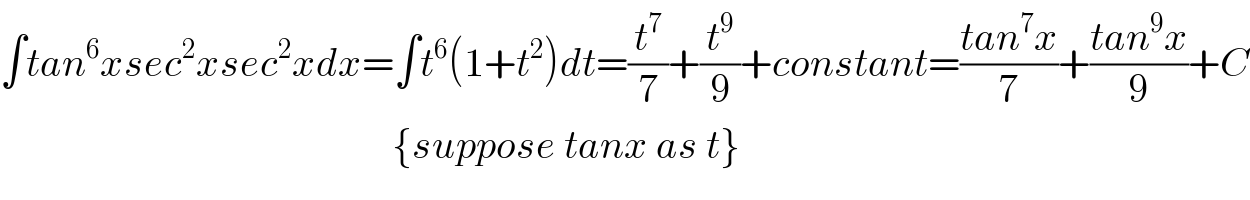
$$\int{tan}^{\mathrm{6}} {xsec}^{\mathrm{2}} {xsec}^{\mathrm{2}} {xdx}=\int{t}^{\mathrm{6}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}=\frac{{t}^{\mathrm{7}} }{\mathrm{7}}+\frac{{t}^{\mathrm{9}} }{\mathrm{9}}+{constant}=\frac{{tan}^{\mathrm{7}} {x}}{\mathrm{7}}+\frac{{tan}^{\mathrm{9}} {x}}{\mathrm{9}}+{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{suppose}\:{tanx}\:{as}\:{t}\right\} \\ $$
Commented by bemath last updated on 23/Jun/20
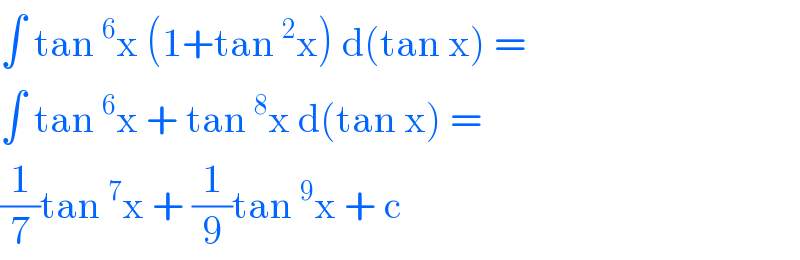
$$\int\:\mathrm{tan}\:^{\mathrm{6}} \mathrm{x}\:\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}\right)\:\mathrm{d}\left(\mathrm{tan}\:\mathrm{x}\right)\:= \\ $$$$\int\:\mathrm{tan}\:^{\mathrm{6}} \mathrm{x}\:+\:\mathrm{tan}\:^{\mathrm{8}} \mathrm{x}\:\mathrm{d}\left(\mathrm{tan}\:\mathrm{x}\right)\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{7}}\mathrm{tan}\:^{\mathrm{7}} \mathrm{x}\:+\:\frac{\mathrm{1}}{\mathrm{9}}\mathrm{tan}\:^{\mathrm{9}} \mathrm{x}\:+\:\mathrm{c}\: \\ $$
Answered by mathmax by abdo last updated on 23/Jun/20
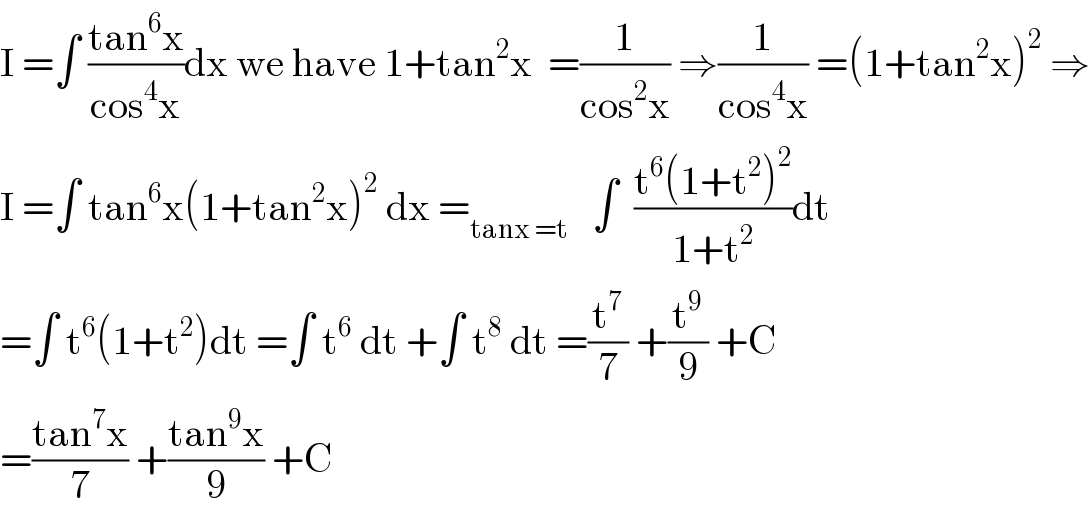
$$\mathrm{I}\:=\int\:\frac{\mathrm{tan}^{\mathrm{6}} \mathrm{x}}{\mathrm{cos}^{\mathrm{4}} \mathrm{x}}\mathrm{dx}\:\mathrm{we}\:\mathrm{have}\:\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\:=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{4}} \mathrm{x}}\:=\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\mathrm{tan}^{\mathrm{6}} \mathrm{x}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} \:\mathrm{dx}\:=_{\mathrm{tanx}\:=\mathrm{t}} \:\:\:\int\:\:\frac{\mathrm{t}^{\mathrm{6}} \left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\int\:\mathrm{t}^{\mathrm{6}} \left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt}\:=\int\:\mathrm{t}^{\mathrm{6}} \:\mathrm{dt}\:+\int\:\mathrm{t}^{\mathrm{8}} \:\mathrm{dt}\:=\frac{\mathrm{t}^{\mathrm{7}} }{\mathrm{7}}\:+\frac{\mathrm{t}^{\mathrm{9}} }{\mathrm{9}}\:+\mathrm{C} \\ $$$$=\frac{\mathrm{tan}^{\mathrm{7}} \mathrm{x}}{\mathrm{7}}\:+\frac{\mathrm{tan}^{\mathrm{9}} \mathrm{x}}{\mathrm{9}}\:+\mathrm{C} \\ $$
