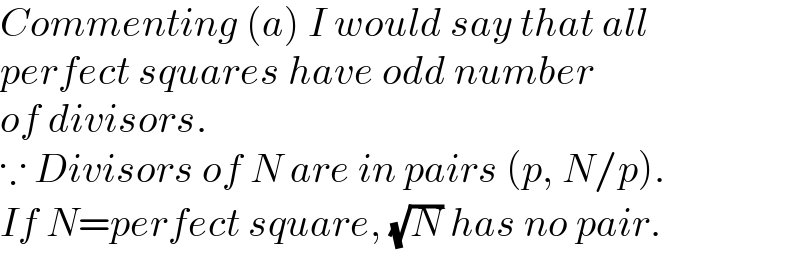Question-a-which-numbers-have-an-odd-number-of-divisors-b-Is-there-a-number-with-exactly-13-divisors-c-Generalize-

Question Number 164300 by otchereabdullai@gmail.com last updated on 16/Jan/22

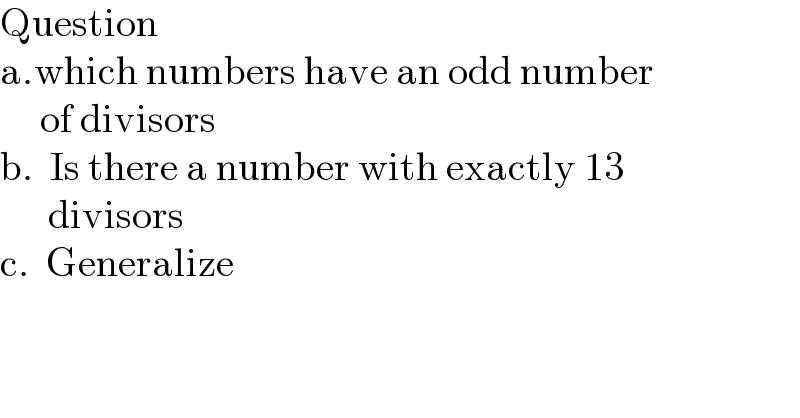
Question

a . which numbers have an odd number

of divisors

b . Is there a number with exactly 13

divisors

c . Generalize

Answered by mr W last updated on 16/Jan/22

a .

a l l n u m b e r s h a v e o d d n u m b e r o f

d i v i s o r s, i f i n t h e i r p r i m e

f a c t o r i z a t i o n a l l e x p o n e n t s a r e

e v e n . i . e . n = p_{1}^{2 k_{1}} p_{2}^{2 k_{2}} p_{3}^{2 k_{3}} \dots w i t h

p_{i} \in P, k_{i} \in N .

t h i s c a n b e e a s i l y c h e c k e d . t h e n u m b e r

o f d i v i s o r s o f n i s

N = (2 k_{1} + 1) (2 k_{2} + 1) (2 k_{3} + 1) \dots

w h i c h i s a l w a y s a n o d d n u m b e r .

b .

y e s!

e . g . 2^{12}, 3^{12}, 11^{12} e t c . h a v e e x a c t l y 13

d i v i s o r s .

w i t h k n o w l e d g e f r o m a b o v e, w e o n l y

n e e d t o f i n d n s u c h t h a t

N = (2 k_{1} + 1) (2 k_{2} + 1) (2 k_{3} + 1) \dots = 13

s i n c e 13 i s p r i m e, t h e r e f o r e t h e o n l y

p o s s i b i l i t y i s k_{1} = 6, k_{⩾ 2} = 0 . t h a t m e a n s

a l l n u m b e r s i n f o r m n = p^{12} h a s e x a c t l y

13 d i v i s o r s, w h e r e p i s a n y p r i m e

n u m b e r .

c .

n = p^{12} w i t h p \in P

Commented by Rasheed.Sindhi last updated on 16/Jan/22

N i c e & E l e g a n t!

Commented by otchereabdullai@gmail.com last updated on 16/Jan/22

God bless you prof W

Commented by Tawa11 last updated on 16/Jan/22

Great sir

Commented by nikif99 last updated on 16/Jan/22

C o m m e n t i n g (a) I w o u l d s a y t h a t a l l

p e r f e c t s q u a r e s h a v e o d d n u m b e r

o f d i v i s o r s .

∵ D i v i s o r s o f N a r e i n p a i r s (p, N / p) .

I f N = p e r f e c t s q u a r e, \sqrt{N} h a s n o p a i r .

Facebook Tweet Pin