Question Number 83719 by Roland Mbunwe last updated on 05/Mar/20
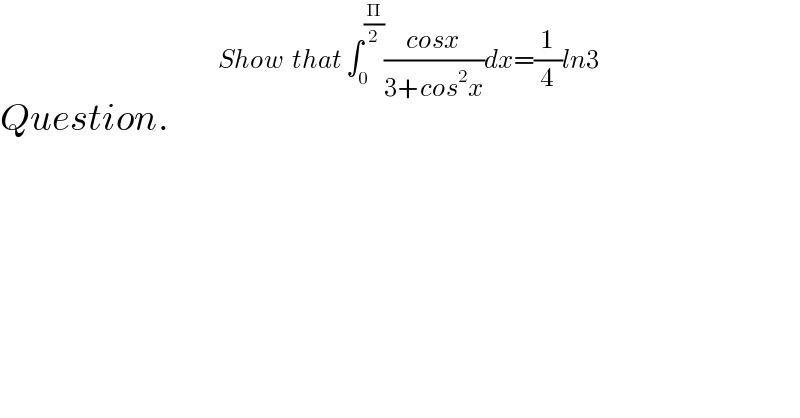
$${Question}.\:\:\:\:\:\:\:\:\overset{{Show}\:\:{that}\:\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{cosx}}{\mathrm{3}+{cos}^{\mathrm{2}} {x}}{dx}=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mathrm{3}} {\:} \\ $$
Commented by mathmax by abdo last updated on 05/Mar/20
![I=∫_0 ^(π/2) ((cosx)/(3+cos^2 x))dx ⇒I =∫_0 ^(π/2) ((cosxdx)/(4−sin^2 x)) =_(sinx =t) ∫_0 ^1 (dt/(4−t^2 )) =(1/4)∫_0 ^1 ((1/(2−t))+(1/(2+t)))dt =(1/4)[ln∣((2+t)/(2−t))∣]_0 ^1 =(1/4)(ln(3)) =(1/4)ln(3)](https://www.tinkutara.com/question/Q83757.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{cosx}}{\mathrm{3}+{cos}^{\mathrm{2}} {x}}{dx}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{cosxdx}}{\mathrm{4}−{sin}^{\mathrm{2}} {x}}\:=_{{sinx}\:={t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{4}−{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}−{t}}+\frac{\mathrm{1}}{\mathrm{2}+{t}}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\mid\frac{\mathrm{2}+{t}}{\mathrm{2}−{t}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{4}}\left({ln}\left(\mathrm{3}\right)\right)\:=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{3}\right) \\ $$
Answered by jagoll last updated on 05/Mar/20
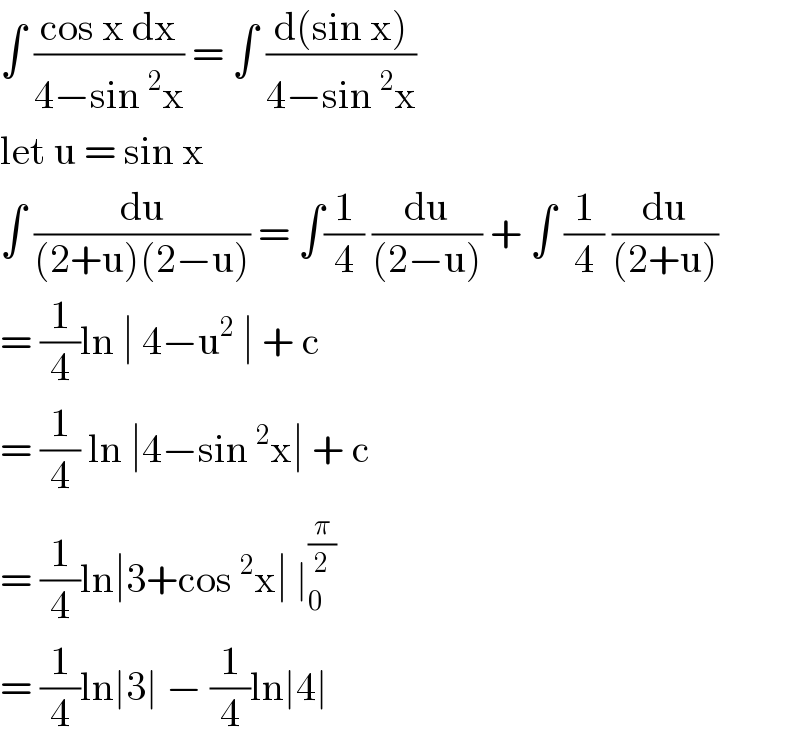
$$\int\:\frac{\mathrm{cos}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{4}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:=\:\int\:\frac{\mathrm{d}\left(\mathrm{sin}\:\mathrm{x}\right)}{\mathrm{4}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$\mathrm{let}\:\mathrm{u}\:=\:\mathrm{sin}\:\mathrm{x} \\ $$$$\int\:\frac{\mathrm{du}}{\left(\mathrm{2}+\mathrm{u}\right)\left(\mathrm{2}−\mathrm{u}\right)}\:=\:\int\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\mathrm{du}}{\left(\mathrm{2}−\mathrm{u}\right)}\:+\:\int\:\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\mathrm{du}}{\left(\mathrm{2}+\mathrm{u}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\mid\:\mathrm{4}−\mathrm{u}^{\mathrm{2}} \:\mid\:+\:\mathrm{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{ln}\:\mid\mathrm{4}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\mid\:+\:\mathrm{c}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{3}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\mid\:\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{3}\mid\:−\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{4}\mid \\ $$
Commented by john santu last updated on 05/Mar/20
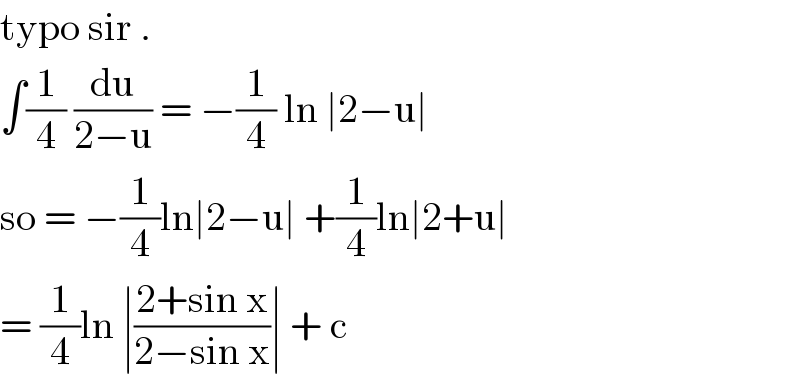
$$\mathrm{typo}\:\mathrm{sir}\:. \\ $$$$\int\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\mathrm{du}}{\mathrm{2}−\mathrm{u}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{ln}\:\mid\mathrm{2}−\mathrm{u}\mid \\ $$$$\mathrm{so}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{2}−\mathrm{u}\mid\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{2}+\mathrm{u}\mid\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\mid\frac{\mathrm{2}+\mathrm{sin}\:\mathrm{x}}{\mathrm{2}−\mathrm{sin}\:\mathrm{x}}\mid\:+\:\mathrm{c} \\ $$
Answered by MJS last updated on 05/Mar/20
![∫((cos x)/(3+cos^2 x))dx= [t=sin x → (dt/(cos x))] =−∫(dt/(t^2 −4))=−(1/4)ln ∣((t−2)/(t+2))∣ = =−(1/4)ln ∣((sin x −2)/(sin x +2))∣ +C ⇒ ∫_0 ^(π/2) ((cos x)/(3+cos^2 x))dx=(1/4)ln 3](https://www.tinkutara.com/question/Q83746.png)
$$\int\frac{\mathrm{cos}\:{x}}{\mathrm{3}+\mathrm{cos}^{\mathrm{2}} \:{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sin}\:{x}\:\rightarrow\:\frac{{dt}}{\mathrm{cos}\:{x}}\right] \\ $$$$=−\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\mid\frac{{t}−\mathrm{2}}{{t}+\mathrm{2}}\mid\:= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\mid\frac{\mathrm{sin}\:{x}\:−\mathrm{2}}{\mathrm{sin}\:{x}\:+\mathrm{2}}\mid\:+{C} \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{cos}\:{x}}{\mathrm{3}+\mathrm{cos}^{\mathrm{2}} \:{x}}{dx}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\mathrm{3} \\ $$
