Question Number 38515 by Rio Mike last updated on 26/Jun/18

$$\:{Question}\:; \\ $$$${x}^{\mathrm{3}} \:+\:{x}^{\mathrm{3}} \:=\: \\ $$$$\left.{A}\right)\:{x}^{\mathrm{9}} \\ $$$$\left.{B}\right)\:{x}^{\mathrm{6}} \\ $$$$\left.{C}\right)\:{x}^{\mathrm{3}} \\ $$$$\left.{D}\right)\:\mathrm{1} \\ $$$${Give}\:{a}\:{reason}\:{for}\:{your}\:{answer}. \\ $$
Answered by MJS last updated on 26/Jun/18
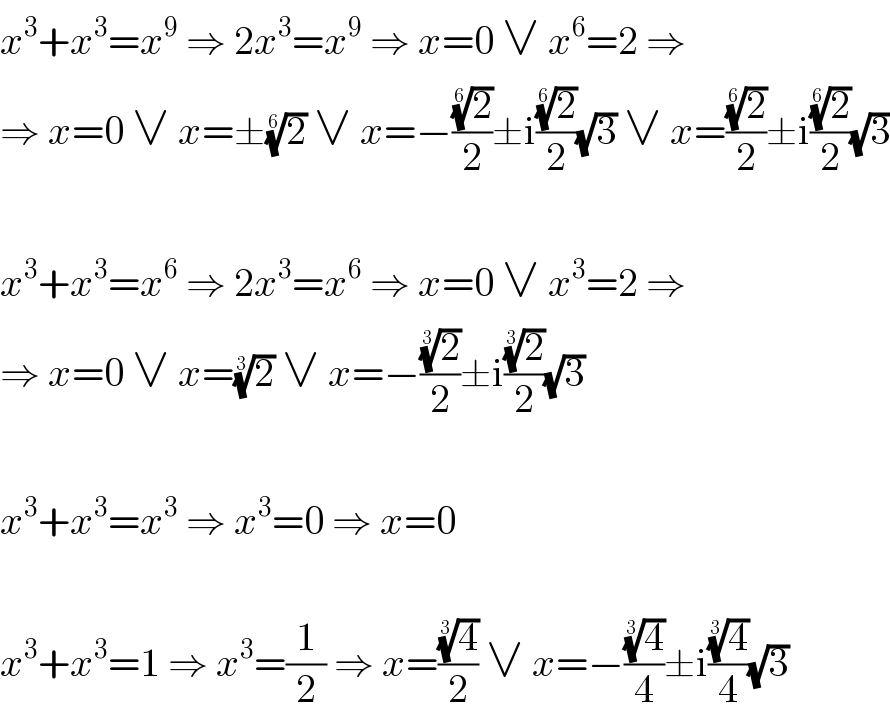
$${x}^{\mathrm{3}} +{x}^{\mathrm{3}} ={x}^{\mathrm{9}} \:\Rightarrow\:\mathrm{2}{x}^{\mathrm{3}} ={x}^{\mathrm{9}} \:\Rightarrow\:{x}=\mathrm{0}\:\vee\:{x}^{\mathrm{6}} =\mathrm{2}\:\Rightarrow \\ $$$$\Rightarrow\:{x}=\mathrm{0}\:\vee\:{x}=\pm\sqrt[{\mathrm{6}}]{\mathrm{2}}\:\vee\:{x}=−\frac{\sqrt[{\mathrm{6}}]{\mathrm{2}}}{\mathrm{2}}\pm\mathrm{i}\frac{\sqrt[{\mathrm{6}}]{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{3}}\:\vee\:{x}=\frac{\sqrt[{\mathrm{6}}]{\mathrm{2}}}{\mathrm{2}}\pm\mathrm{i}\frac{\sqrt[{\mathrm{6}}]{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{3}} \\ $$$$ \\ $$$${x}^{\mathrm{3}} +{x}^{\mathrm{3}} ={x}^{\mathrm{6}} \:\Rightarrow\:\mathrm{2}{x}^{\mathrm{3}} ={x}^{\mathrm{6}} \:\Rightarrow\:{x}=\mathrm{0}\:\vee\:{x}^{\mathrm{3}} =\mathrm{2}\:\Rightarrow \\ $$$$\Rightarrow\:{x}=\mathrm{0}\:\vee\:{x}=\sqrt[{\mathrm{3}}]{\mathrm{2}}\:\vee\:{x}=−\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}}\pm\mathrm{i}\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{3}} \\ $$$$ \\ $$$${x}^{\mathrm{3}} +{x}^{\mathrm{3}} ={x}^{\mathrm{3}} \:\Rightarrow\:{x}^{\mathrm{3}} =\mathrm{0}\:\Rightarrow\:{x}=\mathrm{0} \\ $$$$ \\ $$$${x}^{\mathrm{3}} +{x}^{\mathrm{3}} =\mathrm{1}\:\Rightarrow\:{x}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{x}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{4}}}{\mathrm{2}}\:\vee\:{x}=−\frac{\sqrt[{\mathrm{3}}]{\mathrm{4}}}{\mathrm{4}}\pm\mathrm{i}\frac{\sqrt[{\mathrm{3}}]{\mathrm{4}}}{\mathrm{4}}\sqrt{\mathrm{3}} \\ $$
