Question Number 36837 by Rio Mike last updated on 06/Jun/18

$$\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{2}^{\mathrm{4}{r}−\mathrm{2}} \: \\ $$
Commented by prof Abdo imad last updated on 06/Jun/18
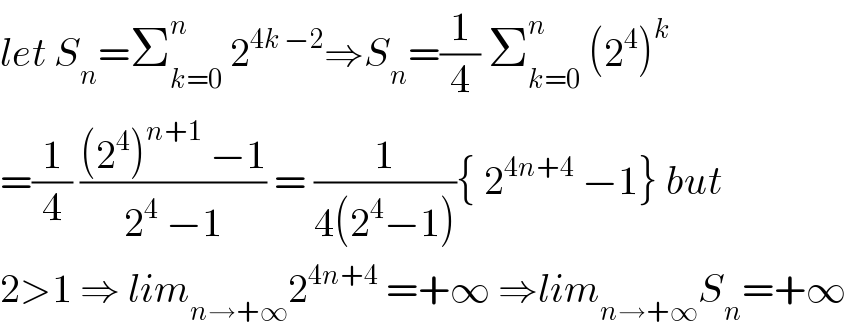
$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\mathrm{2}^{\mathrm{4}{k}\:−\mathrm{2}} \Rightarrow{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(\mathrm{2}^{\mathrm{4}} \right)^{{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\left(\mathrm{2}^{\mathrm{4}} \right)^{{n}+\mathrm{1}} \:−\mathrm{1}}{\mathrm{2}^{\mathrm{4}} \:−\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{2}^{\mathrm{4}} −\mathrm{1}\right)}\left\{\:\mathrm{2}^{\mathrm{4}{n}+\mathrm{4}} \:−\mathrm{1}\right\}\:{but} \\ $$$$\mathrm{2}>\mathrm{1}\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} \mathrm{2}^{\mathrm{4}{n}+\mathrm{4}} \:=+\infty\:\Rightarrow{lim}_{{n}\rightarrow+\infty} {S}_{{n}} =+\infty \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jun/18
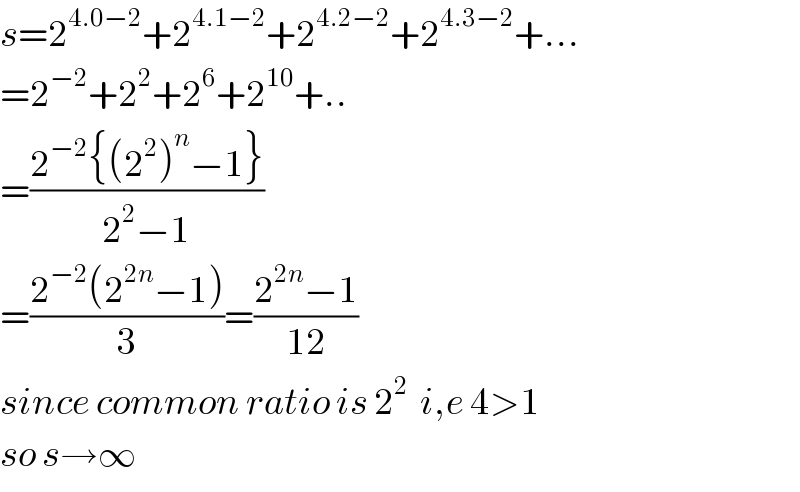
$${s}=\mathrm{2}^{\mathrm{4}.\mathrm{0}−\mathrm{2}} +\mathrm{2}^{\mathrm{4}.\mathrm{1}−\mathrm{2}} +\mathrm{2}^{\mathrm{4}.\mathrm{2}−\mathrm{2}} +\mathrm{2}^{\mathrm{4}.\mathrm{3}−\mathrm{2}} +… \\ $$$$=\mathrm{2}^{−\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{6}} +\mathrm{2}^{\mathrm{10}} +.. \\ $$$$=\frac{\mathrm{2}^{−\mathrm{2}} \left\{\left(\mathrm{2}^{\mathrm{2}} \right)^{{n}} −\mathrm{1}\right\}}{\mathrm{2}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{\mathrm{2}^{−\mathrm{2}} \left(\mathrm{2}^{\mathrm{2}{n}} −\mathrm{1}\right)}{\mathrm{3}}=\frac{\mathrm{2}^{\mathrm{2}{n}} −\mathrm{1}}{\mathrm{12}} \\ $$$${since}\:{common}\:{ratio}\:{is}\:\mathrm{2}^{\mathrm{2}} \:\:{i},{e}\:\mathrm{4}>\mathrm{1} \\ $$$${so}\:{s}\rightarrow\infty \\ $$
