Question Number 151037 by qaz last updated on 17/Aug/21
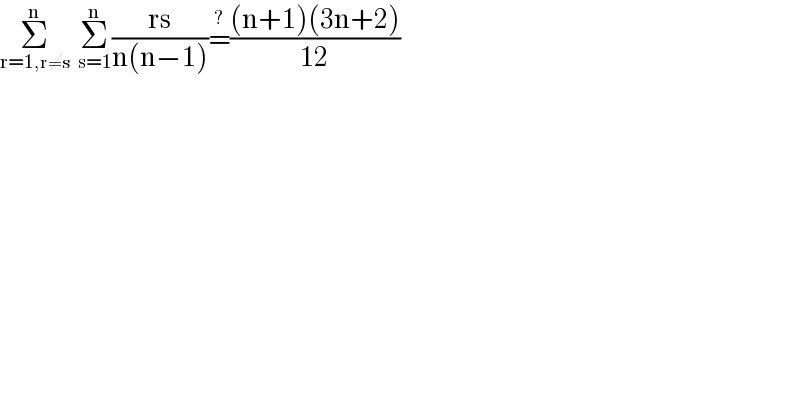
$$\underset{\mathrm{r}=\mathrm{1},\mathrm{r}\neq\mathrm{s}} {\overset{\mathrm{n}} {\sum}}\:\:\underset{\mathrm{s}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{rs}}{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}\overset{?} {=}\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{3n}+\mathrm{2}\right)}{\mathrm{12}} \\ $$
Answered by mindispower last updated on 17/Aug/21
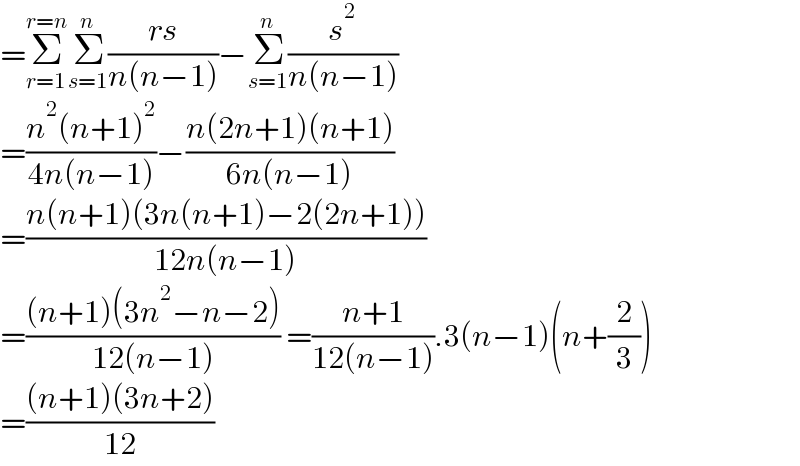
$$=\underset{{r}=\mathrm{1}} {\overset{{r}={n}} {\sum}}\underset{{s}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{rs}}{{n}\left({n}−\mathrm{1}\right)}−\underset{{s}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{s}^{\mathrm{2}} }{{n}\left({n}−\mathrm{1}\right)} \\ $$$$=\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}{n}\left({n}−\mathrm{1}\right)}−\frac{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)\left({n}+\mathrm{1}\right)}{\mathrm{6}{n}\left({n}−\mathrm{1}\right)} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{3}{n}\left({n}+\mathrm{1}\right)−\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)\right)}{\mathrm{12}{n}\left({n}−\mathrm{1}\right)} \\ $$$$=\frac{\left({n}+\mathrm{1}\right)\left(\mathrm{3}{n}^{\mathrm{2}} −{n}−\mathrm{2}\right)}{\mathrm{12}\left({n}−\mathrm{1}\right)}\:=\frac{{n}+\mathrm{1}}{\mathrm{12}\left({n}−\mathrm{1}\right)}.\mathrm{3}\left({n}−\mathrm{1}\right)\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$=\frac{\left({n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}{\mathrm{12}} \\ $$
