R-e-ixt-e-t-2-dt-

Question Number 147166 by puissant last updated on 18/Jul/21

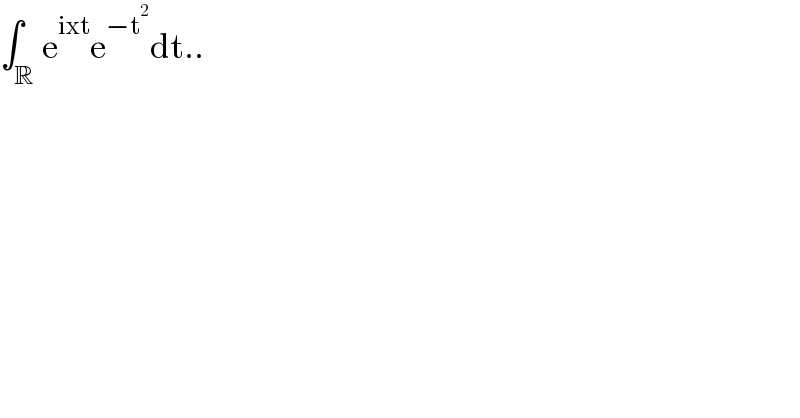
$$\int_{\mathbb{R}} \mathrm{e}^{\mathrm{ixt}} \mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}.. \\ $$

Answered by mathmax by abdo last updated on 18/Jul/21

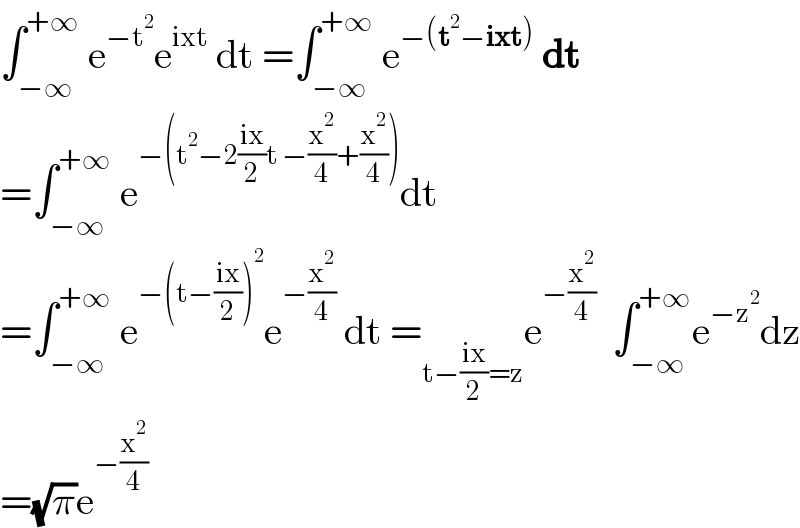
∫_(−∞) ^(+∞) e^(−t^2 ) e^(ixt) dt =∫_(−∞) ^(+∞) e^(−(t^2 −ixt)) dt =∫_(−∞) ^(+∞) e^(−(t^2 −2((ix)/2)t −(x^2 /4)+(x^2 /4))) dt =∫_(−∞) ^(+∞) e^(−(t−((ix)/2))^2 ) e^(−(x^2 /4)) dt =_(t−((ix)/2)=z) e^(−(x^2 /4)) ∫_(−∞) ^(+∞) e^(−z^2 ) dz =(√π)e^(−(x^2 /4))

$$\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{e}^{\mathrm{ixt}} \:\mathrm{dt}\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\left(\boldsymbol{\mathrm{t}}^{\mathrm{2}} −\boldsymbol{\mathrm{ixt}}\right)} \:\boldsymbol{\mathrm{dt}} \\ $$$$=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{ix}}{\mathrm{2}}\mathrm{t}\:−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}\right)} \mathrm{dt} \\ $$$$=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\left(\mathrm{t}−\frac{\mathrm{ix}}{\mathrm{2}}\right)^{\mathrm{2}} } \mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}} \:\mathrm{dt}\:=_{\mathrm{t}−\frac{\mathrm{ix}}{\mathrm{2}}=\mathrm{z}} \mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}} \:\:\int_{−\infty} ^{+\infty} \mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz} \\ $$$$=\sqrt{\pi}\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$

Commented by puissant last updated on 18/Jul/21

$$\mathrm{thanks} \\ $$

Commented by Kamel last updated on 18/Jul/21

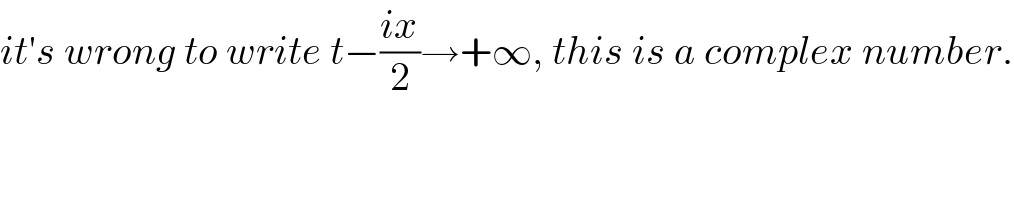
it′s wrong to write t−((ix)/2)→+∞, this is a complex number.

$${it}'{s}\:{wrong}\:{to}\:{write}\:{t}−\frac{{ix}}{\mathrm{2}}\rightarrow+\infty,\:{this}\:{is}\:{a}\:{complex}\:{number}. \\ $$

Commented by mathmax by abdo last updated on 18/Jul/21

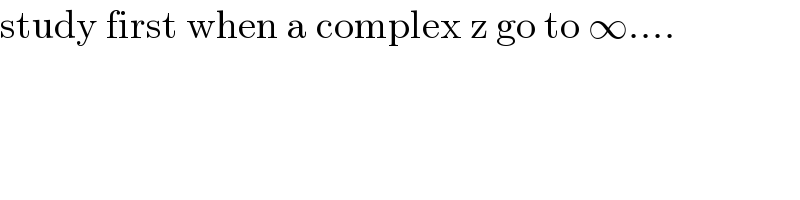
study first when a complex z go to ∞....

$$\mathrm{study}\:\mathrm{first}\:\mathrm{when}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{z}\:\mathrm{go}\:\mathrm{to}\:\infty…. \\ $$

Answered by Kamel last updated on 18/Jul/21

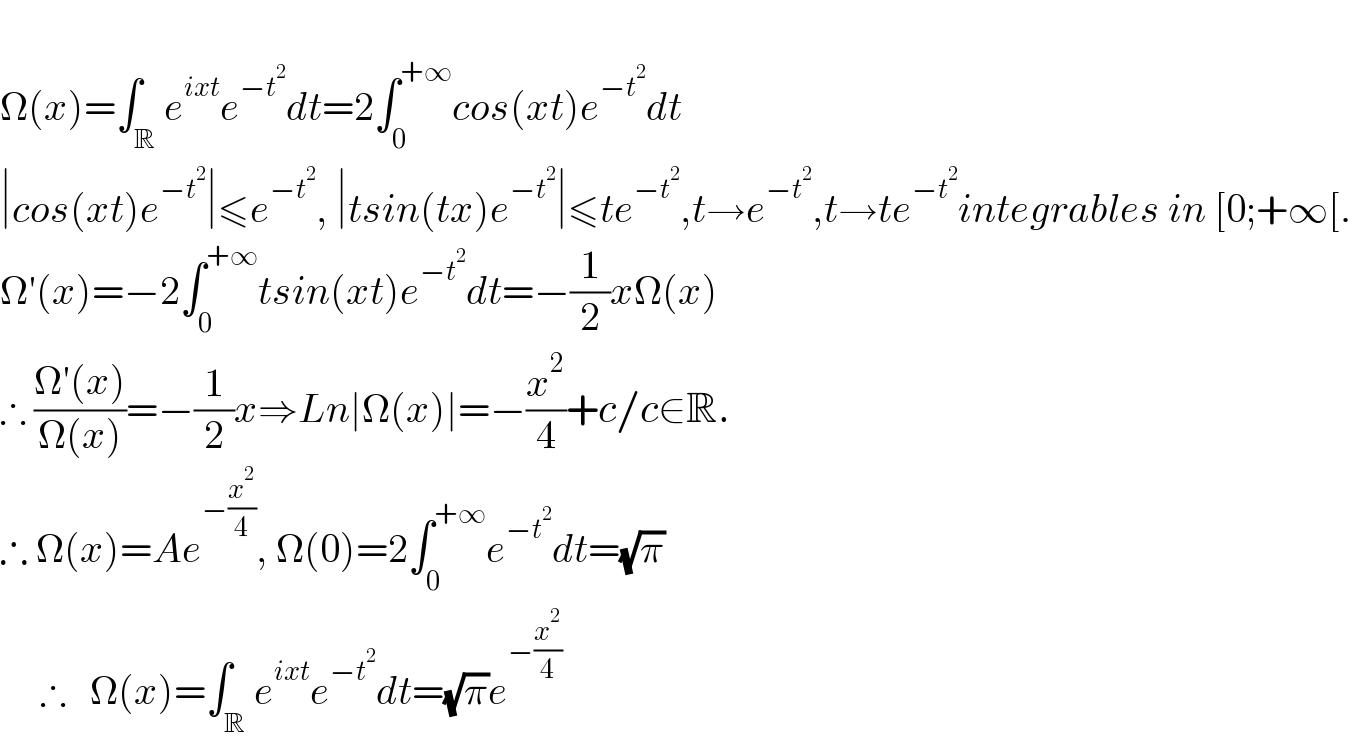
Ω(x)=∫_R e^(ixt) e^(−t^2 ) dt=2∫_0 ^(+∞) cos(xt)e^(−t^2 ) dt ∣cos(xt)e^(−t^2 ) ∣≤e^(−t^2 ) , ∣tsin(tx)e^(−t^2 ) ∣≤te^(−t^2 ) ,t→e^(−t^2 ) ,t→te^(−t^2 ) integrables in [0;+∞[. Ω′(x)=−2∫_0 ^(+∞) tsin(xt)e^(−t^2 ) dt=−(1/2)xΩ(x) ∴ ((Ω′(x))/(Ω(x)))=−(1/2)x⇒Ln∣Ω(x)∣=−(x^2 /4)+c/c∈R. ∴ Ω(x)=Ae^(−(x^2 /4)) , Ω(0)=2∫_0 ^(+∞) e^(−t^2 ) dt=(√π) ∴ Ω(x)=∫_R e^(ixt) e^(−t^2 ) dt=(√π)e^(−(x^2 /4))

$$ \\ $$$$\Omega\left({x}\right)=\int_{\mathbb{R}} {e}^{{ixt}} {e}^{−{t}^{\mathrm{2}} } {dt}=\mathrm{2}\int_{\mathrm{0}} ^{+\infty} {cos}\left({xt}\right){e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$$\mid{cos}\left({xt}\right){e}^{−{t}^{\mathrm{2}} } \mid\leqslant{e}^{−{t}^{\mathrm{2}} } ,\:\mid{tsin}\left({tx}\right){e}^{−{t}^{\mathrm{2}} } \mid\leqslant{te}^{−{t}^{\mathrm{2}} } ,{t}\rightarrow{e}^{−{t}^{\mathrm{2}} } ,{t}\rightarrow{te}^{−{t}^{\mathrm{2}} } {integrables}\:{in}\:\left[\mathrm{0};+\infty\left[.\right.\right. \\ $$$$\Omega'\left({x}\right)=−\mathrm{2}\int_{\mathrm{0}} ^{+\infty} {tsin}\left({xt}\right){e}^{−{t}^{\mathrm{2}} } {dt}=−\frac{\mathrm{1}}{\mathrm{2}}{x}\Omega\left({x}\right) \\ $$$$\therefore\:\frac{\Omega'\left({x}\right)}{\Omega\left({x}\right)}=−\frac{\mathrm{1}}{\mathrm{2}}{x}\Rightarrow{Ln}\mid\Omega\left({x}\right)\mid=−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{c}/{c}\in\mathbb{R}. \\ $$$$\therefore\:\Omega\left({x}\right)={Ae}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} ,\:\Omega\left(\mathrm{0}\right)=\mathrm{2}\int_{\mathrm{0}} ^{+\infty} {e}^{−{t}^{\mathrm{2}} } {dt}=\sqrt{\pi} \\ $$$$\:\:\:\:\:\therefore\:\:\:\Omega\left({x}\right)=\int_{\mathbb{R}} {e}^{{ixt}} {e}^{−{t}^{\mathrm{2}} } {dt}=\sqrt{\pi}{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply