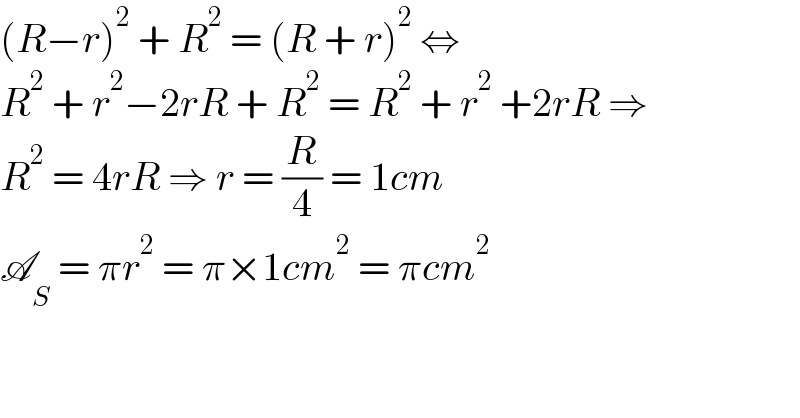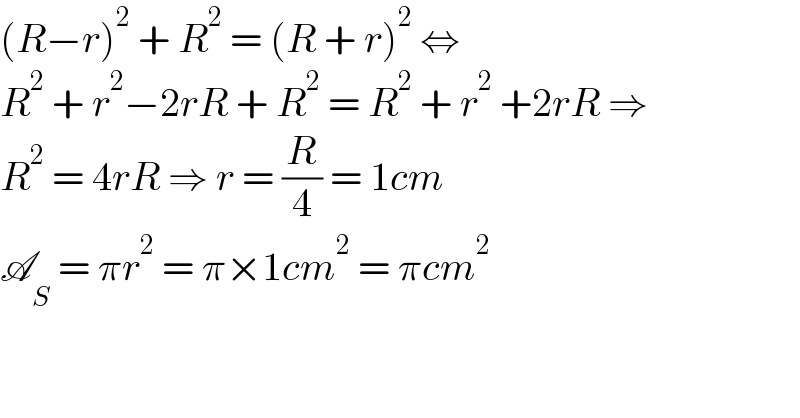R-r-2-R-2-R-r-2-R-2-r-2-2rR-R-2-R-2-r-2-2rR-R-2-4rR-r-R-4-1cm-A-S-pir-2-pi-1cm-2-picm-2-

Question Number 150793 by cherokeesay last updated on 15/Aug/21

$${(R-r)}^2+R^2={(R+r)}^2\iff$$$$R^2+r^2-2rR+R^2=R^2+r^2+2rR\Rightarrow$$$$R^2=4rR\Rightarrow r=\frac{R}{4}=1cm$$$${\mathcal{A}}_S=\pi r^2=\pi \times 1{cm}^2=\pi {cm}^2$$

Commented by Rasheed.Sindhi last updated on 15/Aug/21

$$Nice!$$$$Plwritethisasananswer$$$$ofyourquestion.{Don}^{\prime }tstartnew$$$$threadforananswer.Thanks.$$

Commented by cherokeesay last updated on 15/Aug/21

$$$$the answer to this problem has already been processed by a member (see below) what I have established is my own resolution of this same exercise but accompanied by a diagram! that's all ! good to you.

Terms of Service
Privacy Policy
Contact: info@tinkutara.com