range-of-function-y-x-1-x-3-

Question Number 85425 by john santu last updated on 22/Mar/20

$${range}\:{of}\:{function} \\ $$$${y}\:=\:\frac{\mid{x}−\mathrm{1}\mid}{{x}+\mathrm{3}} \\ $$

Answered by john santu last updated on 22/Mar/20

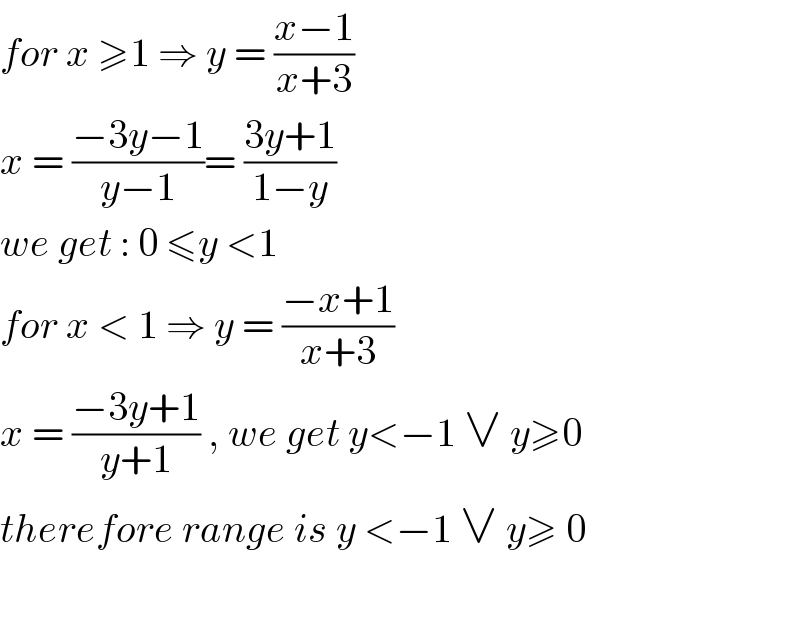
for x ≥1 ⇒ y = ((x−1)/(x+3)) x = ((−3y−1)/(y−1))= ((3y+1)/(1−y)) we get : 0 ≤y <1 for x < 1 ⇒ y = ((−x+1)/(x+3)) x = ((−3y+1)/(y+1)) , we get y<−1 ∨ y≥0 therefore range is y <−1 ∨ y≥ 0

$${for}\:{x}\:\geqslant\mathrm{1}\:\Rightarrow\:{y}\:=\:\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}} \\ $$$${x}\:=\:\frac{−\mathrm{3}{y}−\mathrm{1}}{{y}−\mathrm{1}}=\:\frac{\mathrm{3}{y}+\mathrm{1}}{\mathrm{1}−{y}} \\ $$$${we}\:{get}\::\:\mathrm{0}\:\leqslant{y}\:<\mathrm{1}\: \\ $$$${for}\:{x}\:<\:\mathrm{1}\:\Rightarrow\:{y}\:=\:\frac{−{x}+\mathrm{1}}{{x}+\mathrm{3}} \\ $$$${x}\:=\:\frac{−\mathrm{3}{y}+\mathrm{1}}{{y}+\mathrm{1}}\:,\:{we}\:{get}\:{y}<−\mathrm{1}\:\vee\:{y}\geqslant\mathrm{0} \\ $$$${therefore}\:{range}\:{is}\:{y}\:<−\mathrm{1}\:\vee\:{y}\geqslant\:\mathrm{0} \\ $$$$ \\ $$

Commented by jagoll last updated on 22/Mar/20

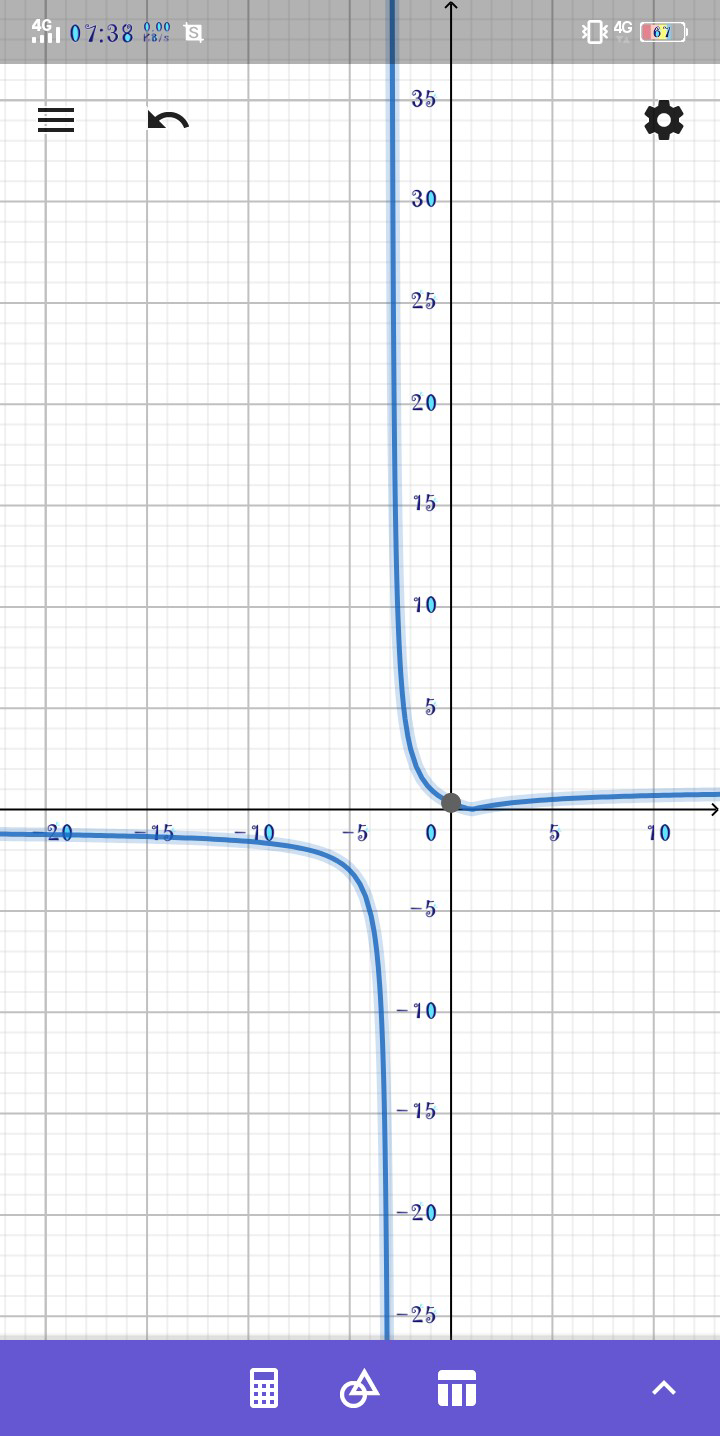
Commented by jagoll last updated on 22/Mar/20

$$\mathrm{this}\:\mathrm{the}\:\mathrm{graph}\: \\ $$

Answered by MJS last updated on 22/Mar/20

y= { ((((1−x)/(x+3))=−1+(4/(x+3)); x<1)),((((x−1)/(x+3))=1−(4/(x+3)); x≥1)) :} range= { ((R_1 =R\[−1; 0])),((R_2 =[0; 1[)) :} range: R=R_1 ∪R_2 =R\[−1;0[ or R=]−∞; −1[ ∪ [0; +∞[

$${y}=\begin{cases}{\frac{\mathrm{1}−{x}}{{x}+\mathrm{3}}=−\mathrm{1}+\frac{\mathrm{4}}{{x}+\mathrm{3}};\:{x}<\mathrm{1}}\\{\frac{{x}−\mathrm{1}}{{x}+\mathrm{3}}=\mathrm{1}−\frac{\mathrm{4}}{{x}+\mathrm{3}};\:{x}\geqslant\mathrm{1}}\end{cases} \\ $$$$\mathrm{range}=\begin{cases}{{R}_{\mathrm{1}} =\mathbb{R}\backslash\left[−\mathrm{1};\:\mathrm{0}\right]}\\{{R}_{\mathrm{2}} =\left[\mathrm{0};\:\mathrm{1}\left[\right.\right.}\end{cases} \\ $$$$\mathrm{range}:\:{R}={R}_{\mathrm{1}} \cup{R}_{\mathrm{2}} =\mathbb{R}\backslash\left[−\mathrm{1};\mathrm{0}\left[\right.\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\mathrm{or}\:{R}=\right]−\infty;\:−\mathrm{1}\left[\:\cup\:\left[\mathrm{0};\:+\infty\left[\right.\right.\right. \\ $$

Commented by john santu last updated on 22/Mar/20

$${my}\:{answer}\:{correct}\:{or}\:{wrong}? \\ $$

Commented by john santu last updated on 22/Mar/20

i don′t understand the notation ]−∞; −1[ ? it same to (−∞,−1) ? sir

$${i}\:{don}'{t}\:{understand}\:{the} \\ $$$$\left.{notation}\:\right]−\infty;\:−\mathrm{1}\left[\:?\right. \\ $$$${it}\:{same}\:{to}\:\left(−\infty,−\mathrm{1}\right)\:?\:{sir} \\ $$

Commented by $@ty@m123 last updated on 22/Mar/20

$${Yeah}. \\ $$$${Both}\:{are}\:{same}. \\ $$

Facebook Tweet Pin

range-of-function-y-x-1-x-3-

Leave a Reply Cancel reply