Question Number 163533 by Ar Brandon last updated on 07/Jan/22
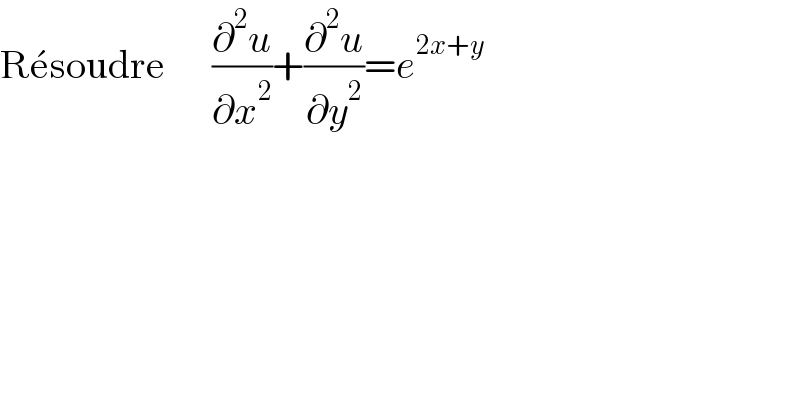
$$\mathrm{R}\acute {\mathrm{e}soudre}\:\:\:\:\:\:\frac{\partial^{\mathrm{2}} {u}}{\partial{x}^{\mathrm{2}} }+\frac{\partial^{\mathrm{2}} {u}}{\partial{y}^{\mathrm{2}} }={e}^{\mathrm{2}{x}+{y}} \\ $$
Commented by Rasheed.Sindhi last updated on 08/Jan/22

$${Welcome}\:{Brandon}\:{sir}\:{with}\:{your} \\ $$$${profile}\:{photo}! \\ $$
Commented by mkam last updated on 08/Jan/22
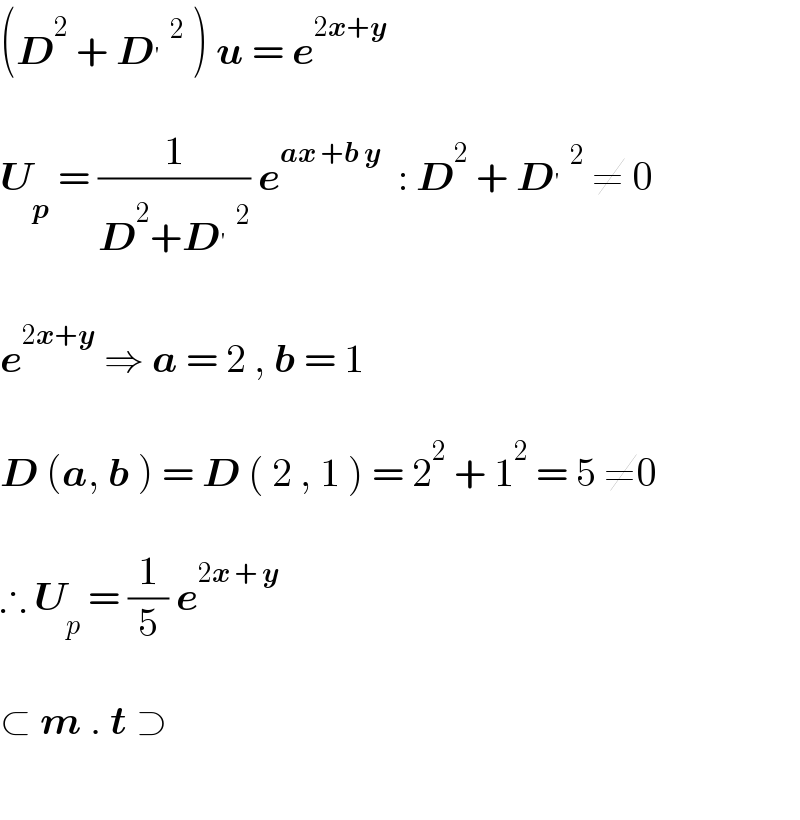
$$\left(\boldsymbol{{D}}^{\mathrm{2}} \:+\:\boldsymbol{{D}}^{'} \:^{\mathrm{2}} \:\right)\:\boldsymbol{{u}}\:=\:\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}+\boldsymbol{{y}}} \\ $$$$ \\ $$$$\boldsymbol{{U}}_{\boldsymbol{{p}}} \:=\:\frac{\mathrm{1}}{\boldsymbol{{D}}^{\mathrm{2}} +\boldsymbol{{D}}^{'} \:^{\mathrm{2}} }\:\boldsymbol{{e}}^{\boldsymbol{{ax}}\:+\boldsymbol{{b}}\:\boldsymbol{{y}}} \:\::\:\boldsymbol{{D}}^{\mathrm{2}} \:+\:\boldsymbol{{D}}^{'} \:^{\mathrm{2}} \:\neq\:\mathrm{0} \\ $$$$ \\ $$$$\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}+\boldsymbol{{y}}} \:\Rightarrow\:\boldsymbol{{a}}\:=\:\mathrm{2}\:,\:\boldsymbol{{b}}\:=\:\mathrm{1} \\ $$$$ \\ $$$$\boldsymbol{{D}}\:\left(\boldsymbol{{a}},\:\boldsymbol{{b}}\:\right)\:=\:\boldsymbol{{D}}\:\left(\:\mathrm{2}\:,\:\mathrm{1}\:\right)\:=\:\mathrm{2}^{\mathrm{2}} \:+\:\mathrm{1}^{\mathrm{2}} \:=\:\mathrm{5}\:\neq\mathrm{0} \\ $$$$ \\ $$$$\therefore\:\boldsymbol{{U}}_{{p}} \:=\:\frac{\mathrm{1}}{\mathrm{5}}\:\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}\:+\:\boldsymbol{{y}}} \\ $$$$ \\ $$$$\subset\:\boldsymbol{{m}}\:.\:\boldsymbol{{t}}\:\supset \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 08/Jan/22
Thanks Sir. But I just realized I omitted a constant in front of e. Sorry!����
Commented by Ar Brandon last updated on 08/Jan/22
Thank you Sir Rasheed ��
Commented by mkam last updated on 08/Jan/22
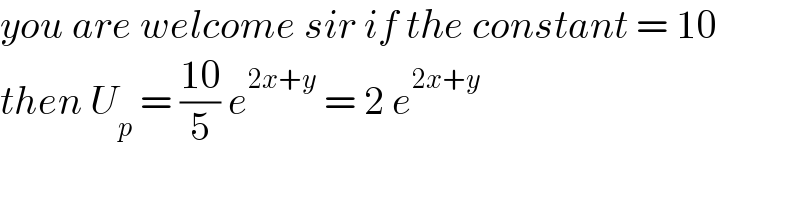
$${you}\:{are}\:{welcome}\:{sir}\:{if}\:{the}\:{constant}\:=\:\mathrm{10}\: \\ $$$${then}\:{U}_{{p}} \:=\:\frac{\mathrm{10}}{\mathrm{5}}\:{e}^{\mathrm{2}{x}+{y}} \:=\:\mathrm{2}\:{e}^{\mathrm{2}{x}+{y}\:} \\ $$
