Question Number 64037 by MJS last updated on 18/Nov/19
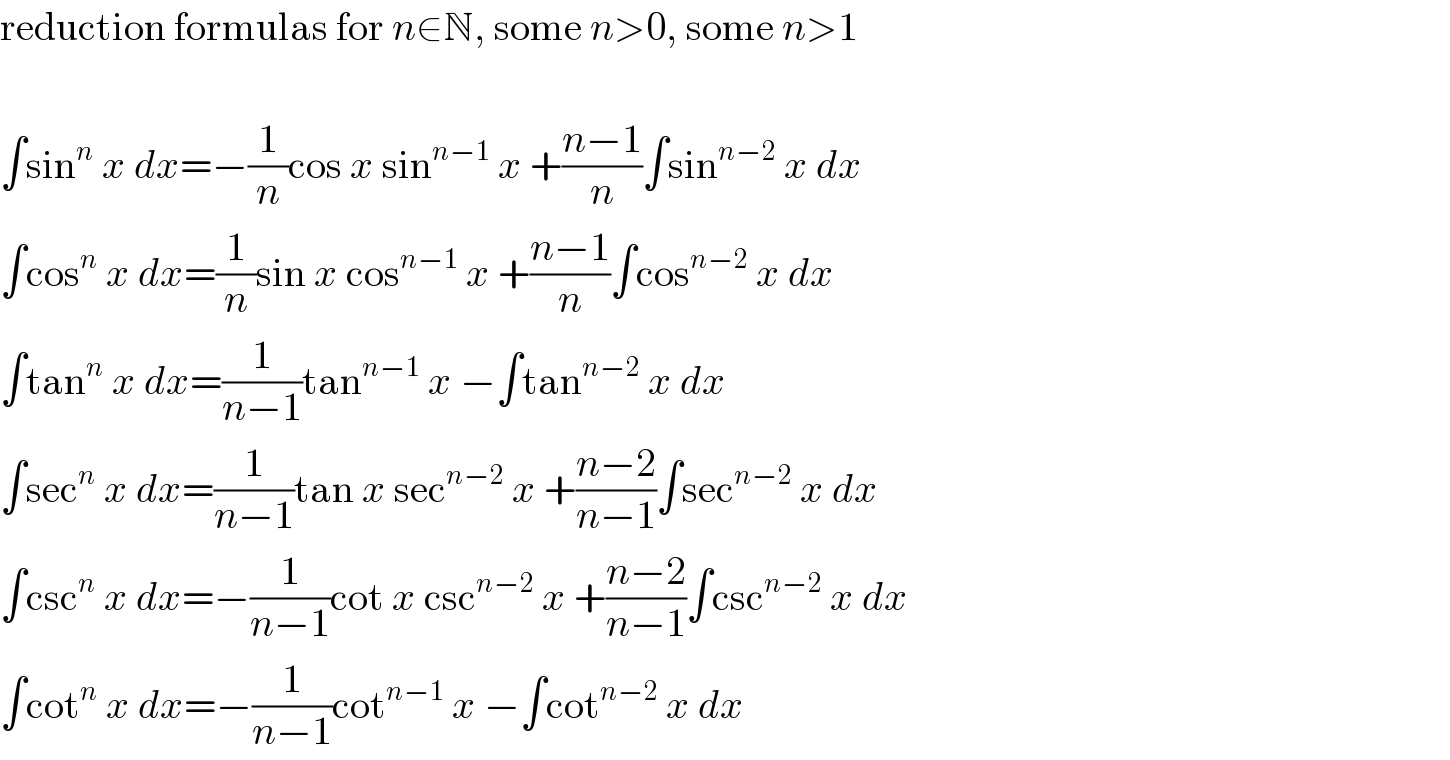
$$\mathrm{reduction}\:\mathrm{formulas}\:\mathrm{for}\:{n}\in\mathbb{N},\:\mathrm{some}\:{n}>\mathrm{0},\:\mathrm{some}\:{n}>\mathrm{1} \\ $$$$ \\ $$$$\int\mathrm{sin}^{{n}} \:{x}\:{dx}=−\frac{\mathrm{1}}{{n}}\mathrm{cos}\:{x}\:\mathrm{sin}^{{n}−\mathrm{1}} \:{x}\:+\frac{{n}−\mathrm{1}}{{n}}\int\mathrm{sin}^{{n}−\mathrm{2}} \:{x}\:{dx} \\ $$$$\int\mathrm{cos}^{{n}} \:{x}\:{dx}=\frac{\mathrm{1}}{{n}}\mathrm{sin}\:{x}\:\mathrm{cos}^{{n}−\mathrm{1}} \:{x}\:+\frac{{n}−\mathrm{1}}{{n}}\int\mathrm{cos}^{{n}−\mathrm{2}} \:{x}\:{dx} \\ $$$$\int\mathrm{tan}^{{n}} \:{x}\:{dx}=\frac{\mathrm{1}}{{n}−\mathrm{1}}\mathrm{tan}^{{n}−\mathrm{1}} \:{x}\:−\int\mathrm{tan}^{{n}−\mathrm{2}} \:{x}\:{dx} \\ $$$$\int\mathrm{sec}^{{n}} \:{x}\:{dx}=\frac{\mathrm{1}}{{n}−\mathrm{1}}\mathrm{tan}\:{x}\:\mathrm{sec}^{{n}−\mathrm{2}} \:{x}\:+\frac{{n}−\mathrm{2}}{{n}−\mathrm{1}}\int\mathrm{sec}^{{n}−\mathrm{2}} \:{x}\:{dx} \\ $$$$\int\mathrm{csc}^{{n}} \:{x}\:{dx}=−\frac{\mathrm{1}}{{n}−\mathrm{1}}\mathrm{cot}\:{x}\:\mathrm{csc}^{{n}−\mathrm{2}} \:{x}\:+\frac{{n}−\mathrm{2}}{{n}−\mathrm{1}}\int\mathrm{csc}^{{n}−\mathrm{2}} \:{x}\:{dx} \\ $$$$\int\mathrm{cot}^{{n}} \:{x}\:{dx}=−\frac{\mathrm{1}}{{n}−\mathrm{1}}\mathrm{cot}^{{n}−\mathrm{1}} \:{x}\:−\int\mathrm{cot}^{{n}−\mathrm{2}} \:{x}\:{dx} \\ $$
Commented by Rio Michael last updated on 12/Jul/19

$${cool}\:{thanks} \\ $$
