Question Number 50511 by behi83417@gmail.com last updated on 17/Dec/18
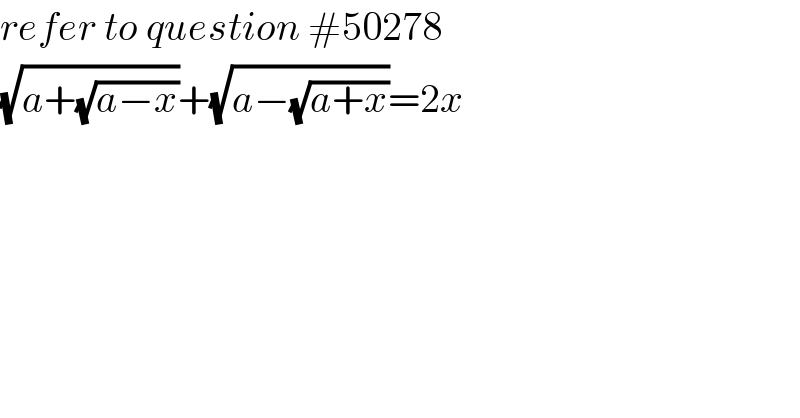
$${refer}\:{to}\:{question}\:#\mathrm{50278} \\ $$$$\sqrt{{a}+\sqrt{{a}−{x}}}+\sqrt{{a}−\sqrt{{a}+{x}}}=\mathrm{2}{x} \\ $$
Answered by behi83417@gmail.com last updated on 17/Dec/18
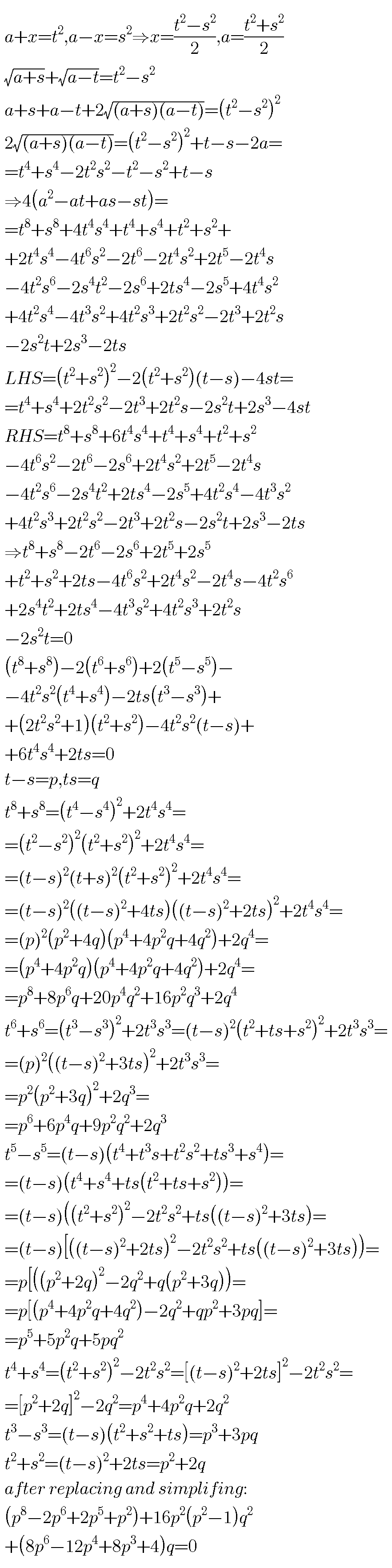
Commented by behi83417@gmail.com last updated on 17/Dec/18
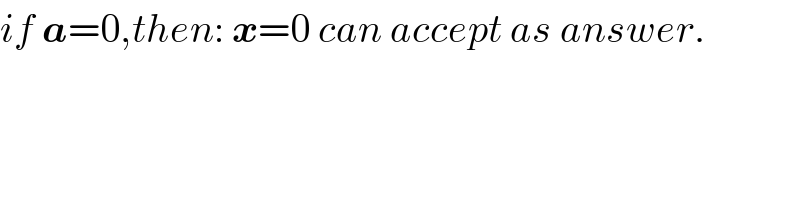
$${if}\:\boldsymbol{{a}}=\mathrm{0},{then}:\:\boldsymbol{{x}}=\mathrm{0}\:{can}\:{accept}\:{as}\:{answer}. \\ $$
Commented by behi83417@gmail.com last updated on 17/Dec/18
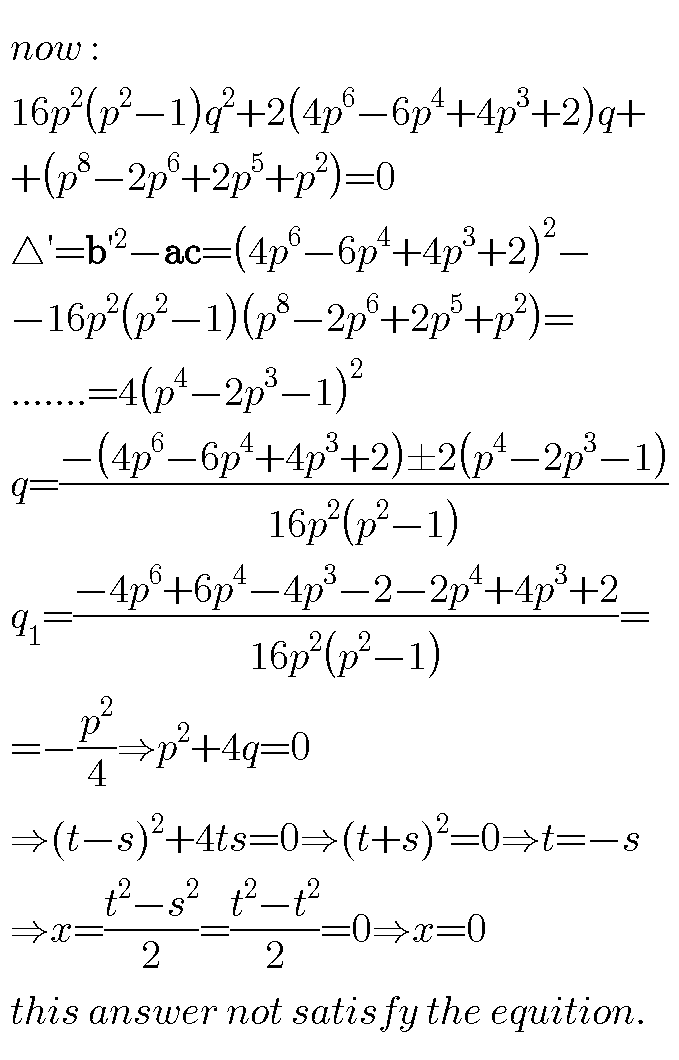
Commented by behi83417@gmail.com last updated on 17/Dec/18
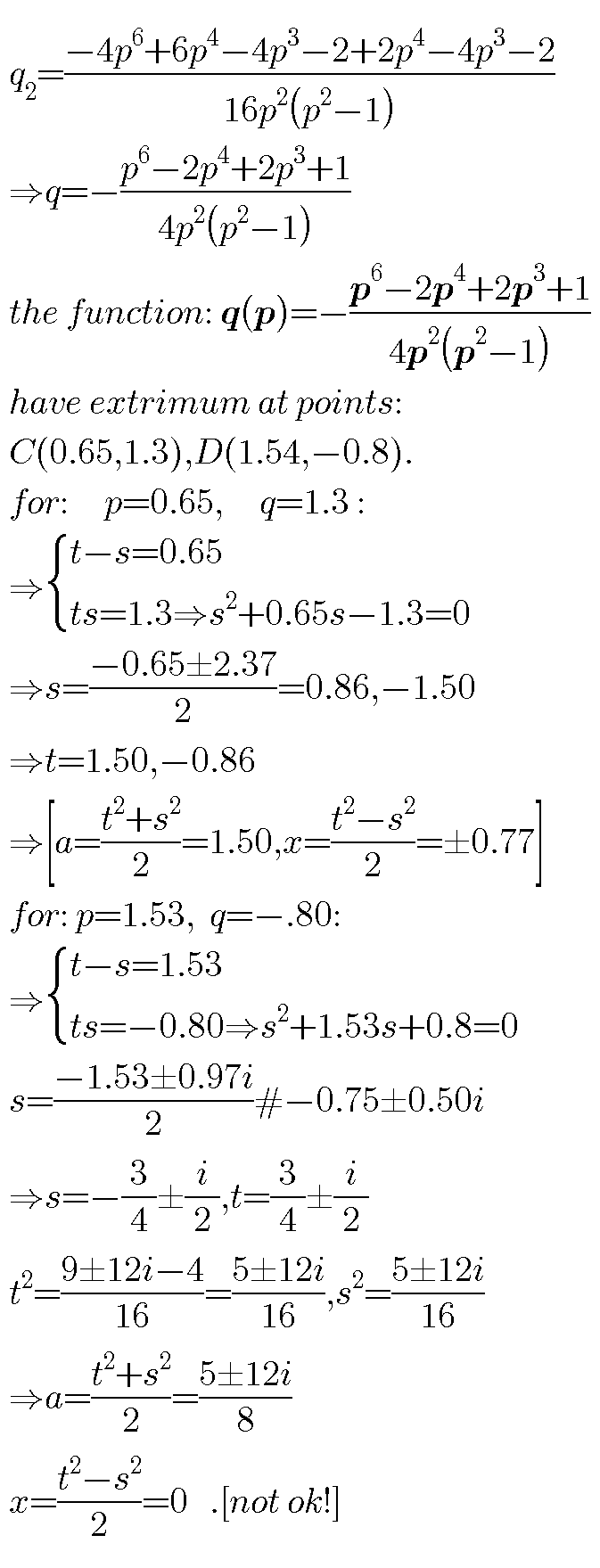
Commented by behi83417@gmail.com last updated on 17/Dec/18
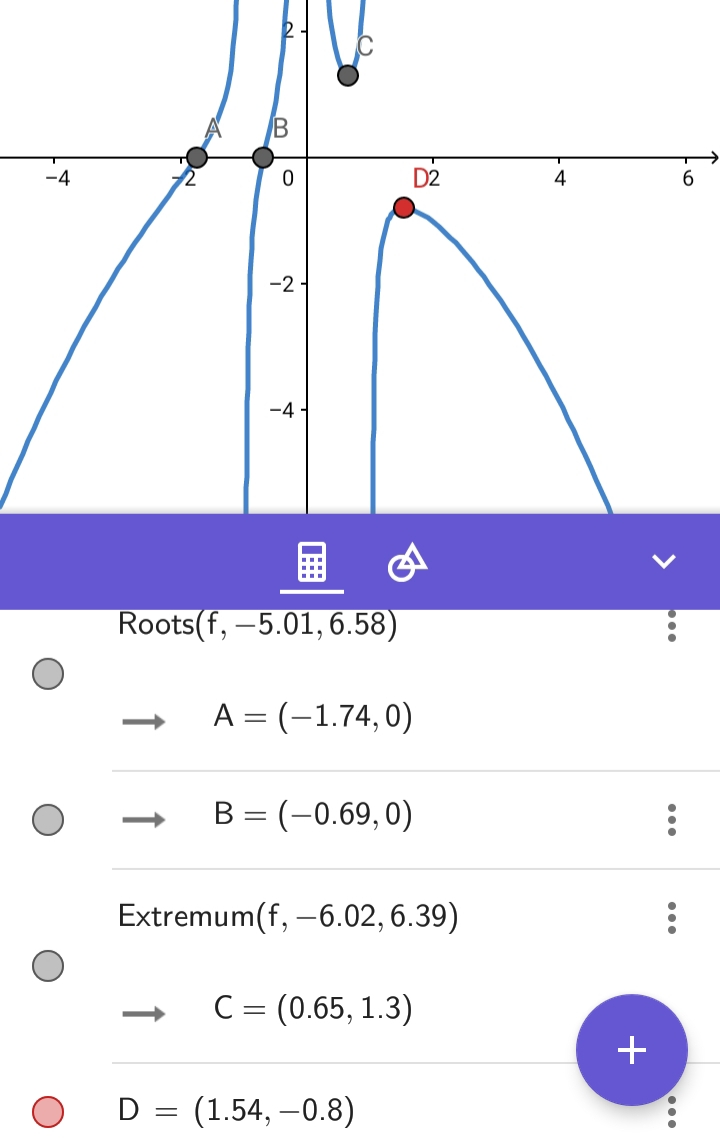
Commented by mr W last updated on 17/Dec/18
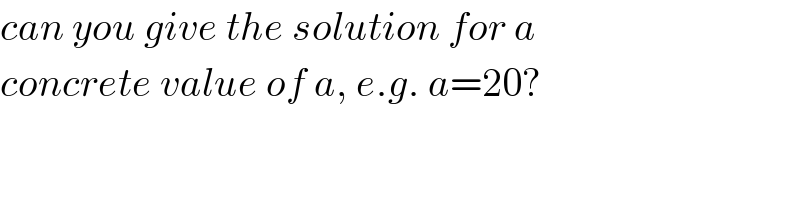
$${can}\:{you}\:{give}\:{the}\:{solution}\:{for}\:{a} \\ $$$${concrete}\:{value}\:{of}\:{a},\:{e}.{g}.\:{a}=\mathrm{20}? \\ $$
Commented by behi83417@gmail.com last updated on 17/Dec/18
![excuse me sir.i cant undrestand this commenet. [concrete=?]](https://www.tinkutara.com/question/Q50597.png)
$${excuse}\:{me}\:{sir}.{i}\:{cant}\:{undrestand}\:{this} \\ $$$${commenet}.\:\:\:\left[{concrete}=?\right] \\ $$
Commented by mr W last updated on 17/Dec/18
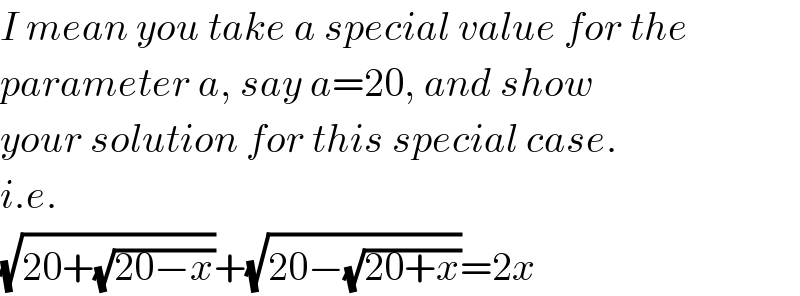
$${I}\:{mean}\:{you}\:{take}\:{a}\:{special}\:{value}\:{for}\:{the} \\ $$$${parameter}\:{a},\:{say}\:{a}=\mathrm{20},\:{and}\:{show} \\ $$$${your}\:{solution}\:{for}\:{this}\:{special}\:{case}. \\ $$$${i}.{e}. \\ $$$$\sqrt{\mathrm{20}+\sqrt{\mathrm{20}−{x}}}+\sqrt{\mathrm{20}−\sqrt{\mathrm{20}+{x}}}=\mathrm{2}{x} \\ $$
Commented by behi83417@gmail.com last updated on 18/Dec/18
![a=20,is too large and big numbers in solution.solve for:a=1 (√(1+(√(1−x))))+(√(1−(√(1+x))))=2x 1+x=t^2 ,1−x=s^2 ⇒x=((t^2 −s^2 )/2),t^2 +s^2 =2 (√(1+s))+(√(1−t))=t^2 −s^2 1+s+1−t+2(√((1+s)(1−t)))=(t^2 −s^2 )^2 4(1+s)(1−t)=[(t^2 −s^2 )^2 +t−s−2]^2 4−4t+4s−4ts=[t^4 +s^4 −2t^2 s^2 +t−s−2]^2 = =t^8 +s^8 +4t^4 s^4 +t^2 +s^2 +4+2t^4 s^4 −4t^6 s^2 +2t^5 −2t^4 s−4t^4 −4t^2 s^6 +2ts^4 −2s^5 −4s^4 −4t^3 s^2 +4t^2 s^3 +4t^2 s^2 −4t+4s−2ts (t^8 +s^8 )+2(t^5 −s^5 )+6t^4 s^4 +2ts+4t^2 s^2 −4t^2 s^2 (t^4 +s^4 )−2ts(t^3 −s^3 )+4(t^4 +s^4 ) −4t^2 s^2 (t−s)=0 (t^8 +s^8 )+2(t^5 −s^5 )−4(1+t^2 s^2 )(t^4 +s^4 ) −2ts(t^3 −s^3 )−4t^2 s^2 (t−s)+6t^4 s^4 + +8t^2 s^2 +2ts+(t^2 +s^2 )=0 let: t−s=p , ts=q t^8 +s^8 =p^8 +8p^6 q+20p^4 q^2 +16p^2 q^3 +2q^4 2(t^5 −s^5 )=2p^5 +10p^2 q+10pq^2 4(1−t^2 s^2 )(t^4 +s^4 )=4(p^4 +4p^2 q+2q^2 )(1−q^2 )= =4p^4 +16p^2 q+8q^2 −4p^4 q^2 −16p^2 q^3 −8q^4 −2ts(t^3 −s^3 )=−2q(p^3 +3pq)= =−2p^3 q−6pq^2 −4t^2 s^2 (t−s)=−4q^2 p −2p^3 q−10pq^2 +2q+4p^4 =0 16p^4 q^2 +2(4p^6 +4p^3 −8p^2 +2)q +(p^8 +2p^5 −4p^4 +p^2 )=0 △′=(4p^6 +4p^3 −8p^2 +2)^2 −16p^4 (p^8 +2p^5 −4p^4 +p^2 )= =4(2p^3 −4p^2 +1)^2 q=((−(4p^6 +4p^3 −8p^2 +2)±2(2p^3 −4p^2 +1))/(16p^4 ))= q_1 =((−4p^6 )/(16p^4 ))=−(p^2 /4) q_2 =−((p^6 +2p^3 −4p^2 +1)/(4p^4 )) for:q=−(p^2 /4)⇒p^2 +4q=0⇒(t−s)^2 +4ts=0 ⇒(t+s)^2 =0⇒t=−s⇒x=0 (not ok!) q(p)=−((p^6 +2p^3 −4p^2 +1)/(4p^4 )),have extrimums at points: E(−.64,1.63),F(.75,.18) p=−.64⇒t−s=−0.64⇒t=s−0.64 q=1.63⇒ts=1.63⇒s(s−.64)=1.63 ⇒s^2 −0.64s−1.63=0⇒s=((.64±2.63)/2) ⇒s=1.64,−1⇒t=1,−1.64 ⇒x=((t^2 −s^2 )/2)=((1.64^2 −1)/2)=±0.84 (√(1+(√(1−0.84))))+(√(1−(√(1+0.84))))= =1.18+0.06i≠2×0.84 (√(1+(√(1+.84))))+(√(1−(√(1−.84))))≠2(−.84) ⇒x=±0.84 not answer. p=0.75⇒t−s=0.75⇒t=s+0.75 ts=.18⇒s(s+.75)=.18 ⇒s^2 +.75s−.18=0⇒s=((−.75±1.13)/2) ⇒s=−.94,0.19 , t=−.19,0.94 x=(((.94)^2 −(.19)^2 )/2)=±0.42 (√(1+(√(1−.42))))+(√(1−(√(1+.42))))≠2×(.42) (√(1+(√(1+.42))))+(√(1−(√(1−.42))))≠2(−.42) ⇒x=±.42 not answer.](https://www.tinkutara.com/question/Q50612.png)
$${a}=\mathrm{20},{is}\:{too}\:{large}\:{and}\:{big}\:{numbers}\:{in} \\ $$$${solution}.{solve}\:{for}:{a}=\mathrm{1} \\ $$$$\sqrt{\mathrm{1}+\sqrt{\mathrm{1}−{x}}}+\sqrt{\mathrm{1}−\sqrt{\mathrm{1}+{x}}}=\mathrm{2}{x} \\ $$$$\mathrm{1}+{x}={t}^{\mathrm{2}} ,\mathrm{1}−{x}={s}^{\mathrm{2}} \Rightarrow{x}=\frac{{t}^{\mathrm{2}} −{s}^{\mathrm{2}} }{\mathrm{2}},{t}^{\mathrm{2}} +{s}^{\mathrm{2}} =\mathrm{2} \\ $$$$\sqrt{\mathrm{1}+{s}}+\sqrt{\mathrm{1}−{t}}={t}^{\mathrm{2}} −{s}^{\mathrm{2}} \\ $$$$\mathrm{1}+{s}+\mathrm{1}−{t}+\mathrm{2}\sqrt{\left(\mathrm{1}+{s}\right)\left(\mathrm{1}−{t}\right)}=\left({t}^{\mathrm{2}} −{s}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{4}\left(\mathrm{1}+{s}\right)\left(\mathrm{1}−{t}\right)=\left[\left({t}^{\mathrm{2}} −{s}^{\mathrm{2}} \right)^{\mathrm{2}} +{t}−{s}−\mathrm{2}\right]^{\mathrm{2}} \\ $$$$\mathrm{4}−\mathrm{4}{t}+\mathrm{4}{s}−\mathrm{4}{ts}=\left[{t}^{\mathrm{4}} +{s}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} {s}^{\mathrm{2}} +{t}−{s}−\mathrm{2}\right]^{\mathrm{2}} = \\ $$$$={t}^{\mathrm{8}} +{s}^{\mathrm{8}} +\mathrm{4}{t}^{\mathrm{4}} {s}^{\mathrm{4}} +{t}^{\mathrm{2}} +{s}^{\mathrm{2}} +\mathrm{4}+\mathrm{2}{t}^{\mathrm{4}} {s}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{6}} {s}^{\mathrm{2}} \\ $$$$+\mathrm{2}{t}^{\mathrm{5}} −\mathrm{2}{t}^{\mathrm{4}} {s}−\mathrm{4}{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} {s}^{\mathrm{6}} +\mathrm{2}{ts}^{\mathrm{4}} −\mathrm{2}{s}^{\mathrm{5}} −\mathrm{4}{s}^{\mathrm{4}} \\ $$$$−\mathrm{4}{t}^{\mathrm{3}} {s}^{\mathrm{2}} +\mathrm{4}{t}^{\mathrm{2}} {s}^{\mathrm{3}} +\mathrm{4}{t}^{\mathrm{2}} {s}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{4}{s}−\mathrm{2}{ts} \\ $$$$\left({t}^{\mathrm{8}} +{s}^{\mathrm{8}} \right)+\mathrm{2}\left({t}^{\mathrm{5}} −{s}^{\mathrm{5}} \right)+\mathrm{6}{t}^{\mathrm{4}} {s}^{\mathrm{4}} +\mathrm{2}{ts}+\mathrm{4}{t}^{\mathrm{2}} {s}^{\mathrm{2}} \\ $$$$−\mathrm{4}{t}^{\mathrm{2}} {s}^{\mathrm{2}} \left({t}^{\mathrm{4}} +{s}^{\mathrm{4}} \right)−\mathrm{2}{ts}\left({t}^{\mathrm{3}} −{s}^{\mathrm{3}} \right)+\mathrm{4}\left({t}^{\mathrm{4}} +{s}^{\mathrm{4}} \right) \\ $$$$−\mathrm{4}{t}^{\mathrm{2}} {s}^{\mathrm{2}} \left({t}−{s}\right)=\mathrm{0} \\ $$$$\left({t}^{\mathrm{8}} +{s}^{\mathrm{8}} \right)+\mathrm{2}\left({t}^{\mathrm{5}} −{s}^{\mathrm{5}} \right)−\mathrm{4}\left(\mathrm{1}+{t}^{\mathrm{2}} {s}^{\mathrm{2}} \right)\left({t}^{\mathrm{4}} +{s}^{\mathrm{4}} \right) \\ $$$$−\mathrm{2}{ts}\left({t}^{\mathrm{3}} −{s}^{\mathrm{3}} \right)−\mathrm{4}{t}^{\mathrm{2}} {s}^{\mathrm{2}} \left({t}−{s}\right)+\mathrm{6}{t}^{\mathrm{4}} {s}^{\mathrm{4}} + \\ $$$$+\mathrm{8}{t}^{\mathrm{2}} {s}^{\mathrm{2}} +\mathrm{2}{ts}+\left({t}^{\mathrm{2}} +{s}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${let}:\:\:\:\:\:\:\boldsymbol{\mathrm{t}}−\boldsymbol{\mathrm{s}}=\boldsymbol{\mathrm{p}}\:\:\:,\:\:\:\boldsymbol{\mathrm{ts}}=\boldsymbol{\mathrm{q}} \\ $$$${t}^{\mathrm{8}} +{s}^{\mathrm{8}} ={p}^{\mathrm{8}} +\mathrm{8}{p}^{\mathrm{6}} {q}+\mathrm{20}{p}^{\mathrm{4}} {q}^{\mathrm{2}} +\mathrm{16}{p}^{\mathrm{2}} {q}^{\mathrm{3}} +\mathrm{2}{q}^{\mathrm{4}} \\ $$$$\mathrm{2}\left({t}^{\mathrm{5}} −{s}^{\mathrm{5}} \right)=\mathrm{2}{p}^{\mathrm{5}} +\mathrm{10}{p}^{\mathrm{2}} {q}+\mathrm{10}{pq}^{\mathrm{2}} \\ $$$$\mathrm{4}\left(\mathrm{1}−{t}^{\mathrm{2}} {s}^{\mathrm{2}} \right)\left({t}^{\mathrm{4}} +{s}^{\mathrm{4}} \right)=\mathrm{4}\left({p}^{\mathrm{4}} +\mathrm{4}{p}^{\mathrm{2}} {q}+\mathrm{2}{q}^{\mathrm{2}} \right)\left(\mathrm{1}−{q}^{\mathrm{2}} \right)= \\ $$$$=\mathrm{4}{p}^{\mathrm{4}} +\mathrm{16}{p}^{\mathrm{2}} {q}+\mathrm{8}{q}^{\mathrm{2}} −\mathrm{4}{p}^{\mathrm{4}} {q}^{\mathrm{2}} −\mathrm{16}{p}^{\mathrm{2}} {q}^{\mathrm{3}} −\mathrm{8}{q}^{\mathrm{4}} \\ $$$$−\mathrm{2}{ts}\left({t}^{\mathrm{3}} −{s}^{\mathrm{3}} \right)=−\mathrm{2}{q}\left({p}^{\mathrm{3}} +\mathrm{3}{pq}\right)= \\ $$$$=−\mathrm{2}{p}^{\mathrm{3}} {q}−\mathrm{6}{pq}^{\mathrm{2}} \\ $$$$−\mathrm{4}{t}^{\mathrm{2}} {s}^{\mathrm{2}} \left({t}−{s}\right)=−\mathrm{4}{q}^{\mathrm{2}} {p} \\ $$$$−\mathrm{2}{p}^{\mathrm{3}} {q}−\mathrm{10}{pq}^{\mathrm{2}} +\mathrm{2}{q}+\mathrm{4}{p}^{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{16}{p}^{\mathrm{4}} {q}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{4}{p}^{\mathrm{6}} +\mathrm{4}{p}^{\mathrm{3}} −\mathrm{8}{p}^{\mathrm{2}} +\mathrm{2}\right){q} \\ $$$$+\left({p}^{\mathrm{8}} +\mathrm{2}{p}^{\mathrm{5}} −\mathrm{4}{p}^{\mathrm{4}} +{p}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\bigtriangleup'=\left(\mathrm{4}{p}^{\mathrm{6}} +\mathrm{4}{p}^{\mathrm{3}} −\mathrm{8}{p}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} −\mathrm{16}{p}^{\mathrm{4}} \left({p}^{\mathrm{8}} +\mathrm{2}{p}^{\mathrm{5}} −\mathrm{4}{p}^{\mathrm{4}} +{p}^{\mathrm{2}} \right)= \\ $$$$=\mathrm{4}\left(\mathrm{2}{p}^{\mathrm{3}} −\mathrm{4}{p}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$${q}=\frac{−\left(\mathrm{4}{p}^{\mathrm{6}} +\mathrm{4}{p}^{\mathrm{3}} −\mathrm{8}{p}^{\mathrm{2}} +\mathrm{2}\right)\pm\mathrm{2}\left(\mathrm{2}{p}^{\mathrm{3}} −\mathrm{4}{p}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{16}{p}^{\mathrm{4}} }= \\ $$$${q}_{\mathrm{1}} =\frac{−\mathrm{4}{p}^{\mathrm{6}} }{\mathrm{16}{p}^{\mathrm{4}} }=−\frac{{p}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${q}_{\mathrm{2}} =−\frac{{p}^{\mathrm{6}} +\mathrm{2}{p}^{\mathrm{3}} −\mathrm{4}{p}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4}{p}^{\mathrm{4}} } \\ $$$${for}:{q}=−\frac{{p}^{\mathrm{2}} }{\mathrm{4}}\Rightarrow{p}^{\mathrm{2}} +\mathrm{4}{q}=\mathrm{0}\Rightarrow\left({t}−{s}\right)^{\mathrm{2}} +\mathrm{4}{ts}=\mathrm{0} \\ $$$$\Rightarrow\left({t}+{s}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow{t}=−{s}\Rightarrow{x}=\mathrm{0}\:\left({not}\:{ok}!\right) \\ $$$${q}\left({p}\right)=−\frac{{p}^{\mathrm{6}} +\mathrm{2}{p}^{\mathrm{3}} −\mathrm{4}{p}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4}{p}^{\mathrm{4}} },{have}\:{extrimums} \\ $$$${at}\:{points}:\:{E}\left(−.\mathrm{64},\mathrm{1}.\mathrm{63}\right),{F}\left(.\mathrm{75},.\mathrm{18}\right) \\ $$$${p}=−.\mathrm{64}\Rightarrow{t}−{s}=−\mathrm{0}.\mathrm{64}\Rightarrow{t}={s}−\mathrm{0}.\mathrm{64} \\ $$$${q}=\mathrm{1}.\mathrm{63}\Rightarrow{ts}=\mathrm{1}.\mathrm{63}\Rightarrow{s}\left({s}−.\mathrm{64}\right)=\mathrm{1}.\mathrm{63} \\ $$$$\Rightarrow{s}^{\mathrm{2}} −\mathrm{0}.\mathrm{64}{s}−\mathrm{1}.\mathrm{63}=\mathrm{0}\Rightarrow{s}=\frac{.\mathrm{64}\pm\mathrm{2}.\mathrm{63}}{\mathrm{2}} \\ $$$$\Rightarrow{s}=\mathrm{1}.\mathrm{64},−\mathrm{1}\Rightarrow{t}=\mathrm{1},−\mathrm{1}.\mathrm{64} \\ $$$$\Rightarrow{x}=\frac{{t}^{\mathrm{2}} −{s}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{1}.\mathrm{64}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}=\pm\mathrm{0}.\mathrm{84} \\ $$$$\sqrt{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{0}.\mathrm{84}}}+\sqrt{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{0}.\mathrm{84}}}= \\ $$$$=\mathrm{1}.\mathrm{18}+\mathrm{0}.\mathrm{06}{i}\neq\mathrm{2}×\mathrm{0}.\mathrm{84} \\ $$$$\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+.\mathrm{84}}}+\sqrt{\mathrm{1}−\sqrt{\mathrm{1}−.\mathrm{84}}}\neq\mathrm{2}\left(−.\mathrm{84}\right) \\ $$$$\Rightarrow{x}=\pm\mathrm{0}.\mathrm{84}\:{not}\:{answer}. \\ $$$${p}=\mathrm{0}.\mathrm{75}\Rightarrow{t}−{s}=\mathrm{0}.\mathrm{75}\Rightarrow{t}={s}+\mathrm{0}.\mathrm{75} \\ $$$${ts}=.\mathrm{18}\Rightarrow{s}\left({s}+.\mathrm{75}\right)=.\mathrm{18} \\ $$$$\Rightarrow{s}^{\mathrm{2}} +.\mathrm{75}{s}−.\mathrm{18}=\mathrm{0}\Rightarrow{s}=\frac{−.\mathrm{75}\pm\mathrm{1}.\mathrm{13}}{\mathrm{2}} \\ $$$$\Rightarrow{s}=−.\mathrm{94},\mathrm{0}.\mathrm{19}\:\:,\:\:{t}=−.\mathrm{19},\mathrm{0}.\mathrm{94} \\ $$$${x}=\frac{\left(.\mathrm{94}\right)^{\mathrm{2}} −\left(.\mathrm{19}\right)^{\mathrm{2}} }{\mathrm{2}}=\pm\mathrm{0}.\mathrm{42} \\ $$$$\sqrt{\mathrm{1}+\sqrt{\mathrm{1}−.\mathrm{42}}}+\sqrt{\mathrm{1}−\sqrt{\mathrm{1}+.\mathrm{42}}}\neq\mathrm{2}×\left(.\mathrm{42}\right) \\ $$$$\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+.\mathrm{42}}}+\sqrt{\mathrm{1}−\sqrt{\mathrm{1}−.\mathrm{42}}}\neq\mathrm{2}\left(−.\mathrm{42}\right) \\ $$$$\Rightarrow{x}=\pm.\mathrm{42}\:\:\:{not}\:\:{answer}. \\ $$
Commented by mr W last updated on 18/Dec/18

$${what}\:{is}\:{the}\:{solution}?\:{i}\:{think}\:{for}\:{a}=\mathrm{1} \\ $$$${there}\:{is}\:{no}\:{solution}. \\ $$
Commented by behi83417@gmail.com last updated on 18/Dec/18
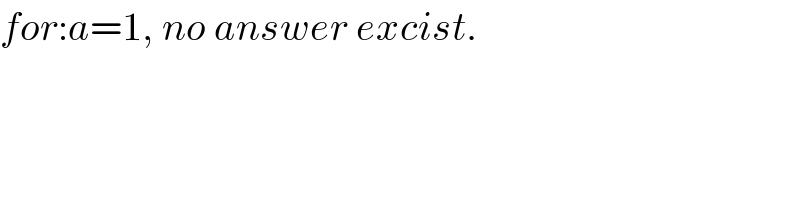
$${for}:{a}=\mathrm{1},\:{no}\:{answer}\:{excist}. \\ $$
