Question Number 16302 by mrW1 last updated on 20/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

Commented by mrW1 last updated on 20/Jun/17
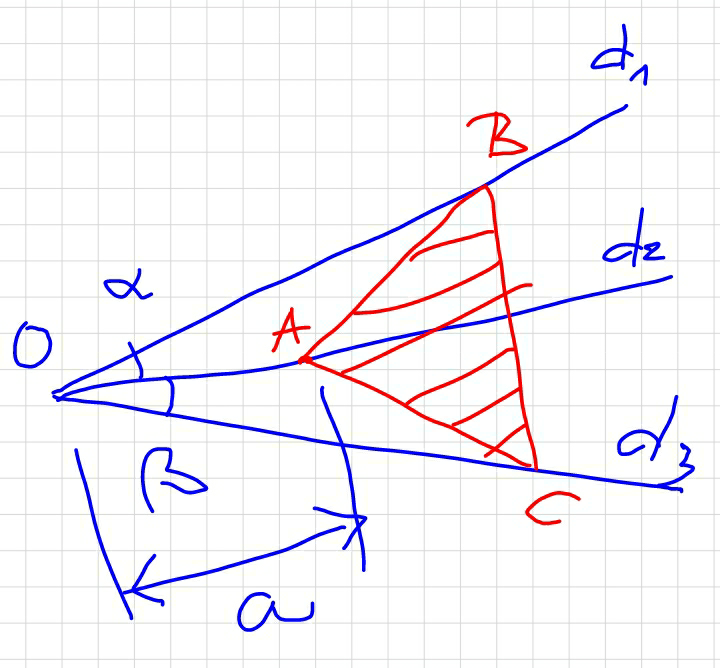
Commented by mrW1 last updated on 20/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17
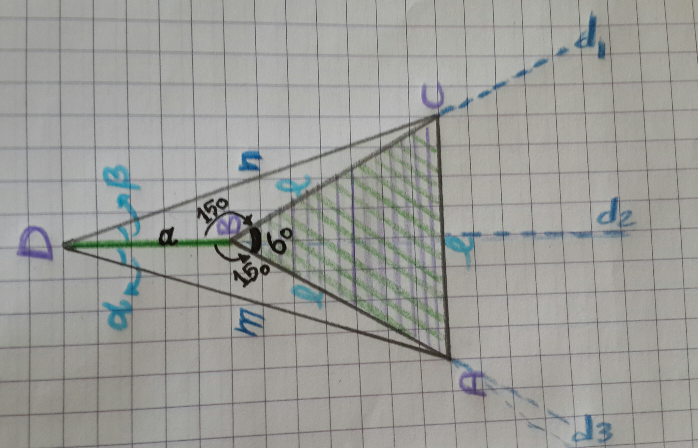
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17
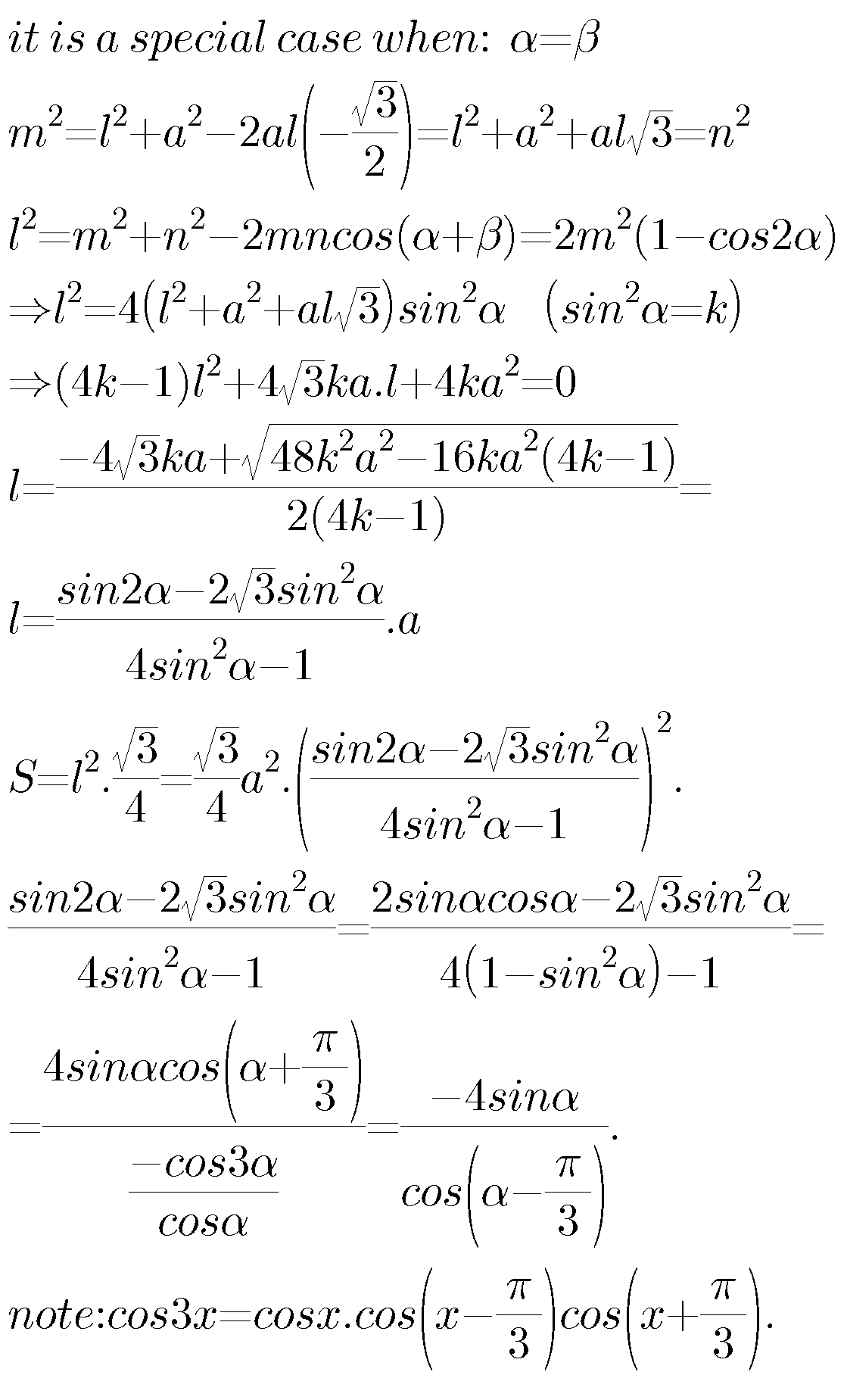
Answered by ajfour last updated on 21/Jun/17
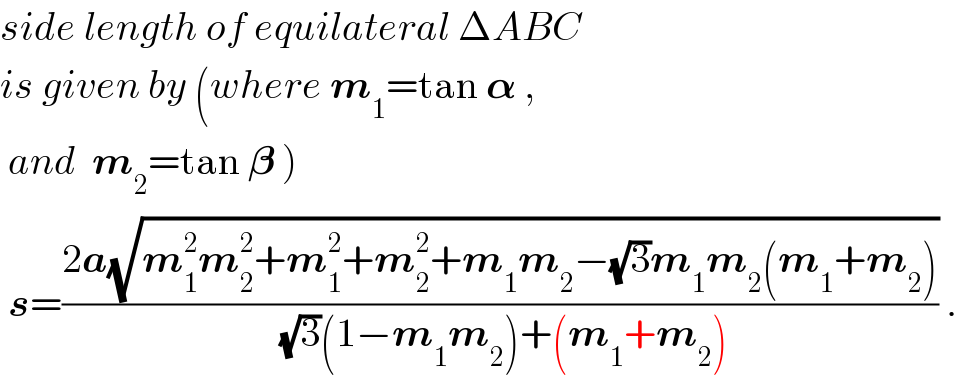
Commented by ajfour last updated on 20/Jun/17

Commented by ajfour last updated on 20/Jun/17
![A is taken on the right. ∠OAB =θ , ∠OAC = π/3−θ tan α = ((s sin θ)/(a−s cos θ)) = m_1 ...(i) tan β = ((s sin (π/3−θ))/(a−s cos (π/3−θ))) = m_2 ...(ii) from (i): s sin θ=am_1 −sm_1 cos θ s=((am_1 )/(sin θ+m_1 cos θ)) ...=(iii) from (ii): s=((am_2 )/(sin (π/3−θ)+m_2 cos (π/3−θ))) ....(iv) we shall find s from (iii) when we find 𝛉 . And to find 𝛉 we shall equate (iii) and (iv) : m_1 [sin (π/3−θ)+m_2 cos (π/3−θ)] =m_2 [sin θ+m_1 cos θ] m_1 [((√3)/2)cos θ−((sin θ)/2)]+m_1 m_2 [((cos θ)/2)+(((√3)sin θ)/2)] =m_2 sin θ+m_1 m_2 cos θ (cos θ)[(((√3)m_1 )/2) − ((m_1 m_2 )/2)]= (sin θ)[(m_1 /2)−((m_1 m_2 (√3))/2)+m_2 ] ((sin θ)/(cos θ))=((m_1 ((√3)−m_2 ))/(m_1 +2m_2 −(√3)m_1 m_2 )) = (p/b) From (iii) s=((am_1 )/(sin 𝛉+m_1 cos 𝛉)) = ((am_1 (√(p^2 +b^2 )))/(p+m_1 b)) =((am_1 (√(p^2 +b^2 )))/(m_1 ((√3)−m_2 )+m_1 (m_1 +2m_2 −(√3)m_1 m_2 ))) =((a (√(p^2 +b^2 )))/( (√3)(1−m_1 m_2 )+(m_1 +m_2 ))) (√(p^2 +b^2 )) comes out to be =2(√((m_1 ^2 m_2 ^2 +m_1 ^2 +m_2 ^2 +m_1 m_2 −(√3)m_1 m_2 (m_1 +m_2 ))) s =((2a(√(m_1 ^2 m_2 ^2 +m_1 ^2 +m_2 ^2 +m_1 m_2 −(√3)m_1 m_2 (m_1 +m_2 ))))/( (√3)(1−m_1 m_2 )+(m_1 +m_2 ))) To locate B and C we need only to draw AB and AC at angles 𝛉 and (𝛑/3−𝛉 ) with AO respectively from point A. Then we join BC. 𝛉=tan^(−1) (((m_1 ((√3)−m_2 ))/(m_1 +2m_2 −(√3)m_1 m_2 ))) The ΔABC is now in place and equilateral .](https://www.tinkutara.com/question/Q16324.png)
Commented by ajfour last updated on 20/Jun/17
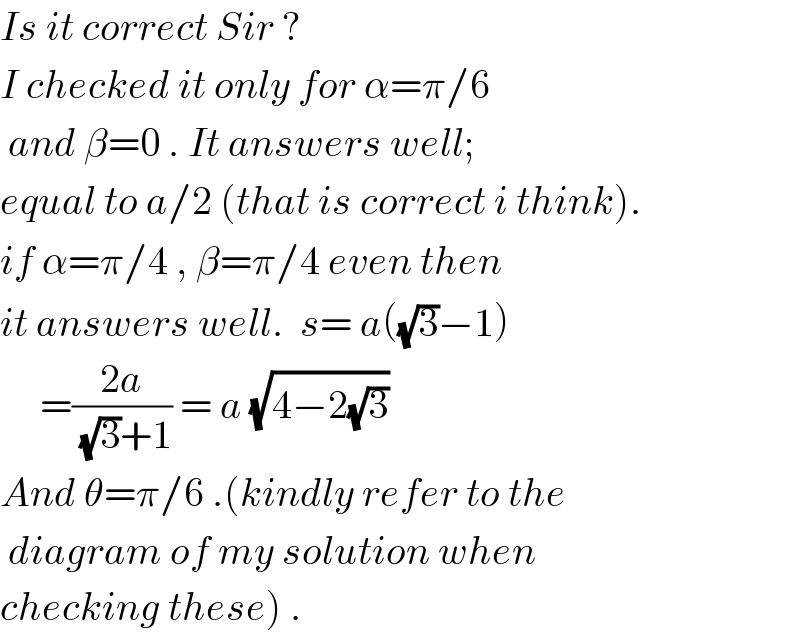
Commented by mrW1 last updated on 20/Jun/17

Commented by mrW1 last updated on 21/Jun/17

Commented by mrW1 last updated on 20/Jun/17
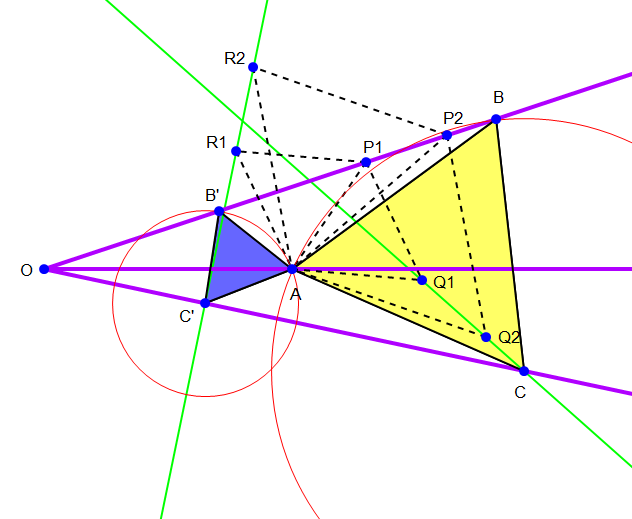
Commented by ajfour last updated on 20/Jun/17

Commented by mrW1 last updated on 21/Jun/17

Commented by ajfour last updated on 21/Jun/17
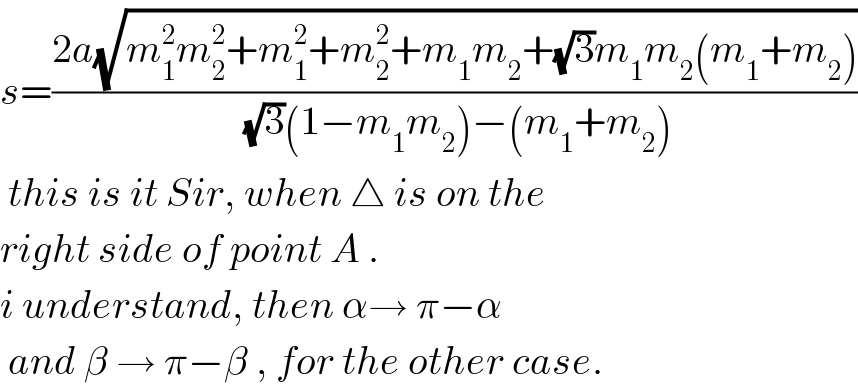
Commented by mrW1 last updated on 21/Jun/17

