Menu Close

repost-question-from-mr-jagoll-2-6y-x-y-x-2y-x-x-2y-x-3y-2-

Tinku Tara 0 Comments
Pin




Question Number 91786 by john santu last updated on 03/May/20
repost question from mr jagoll { ((2+6y = (x/y)−(√(x−2y)))),(((√(x+(√(x−2y)))) = x+3y−2 )) :}
$${repost}\:{question}\:{from} \\ $$$${mr}\:{jagoll} \\ $$$$\begin{cases}{\mathrm{2}+\mathrm{6}{y}\:=\:\frac{{x}}{{y}}−\sqrt{{x}−\mathrm{2}{y}}}\\{\sqrt{{x}+\sqrt{{x}−\mathrm{2}{y}}}\:=\:{x}+\mathrm{3}{y}−\mathrm{2}\:}\end{cases} \\ $$
Commented by john santu last updated on 03/May/20
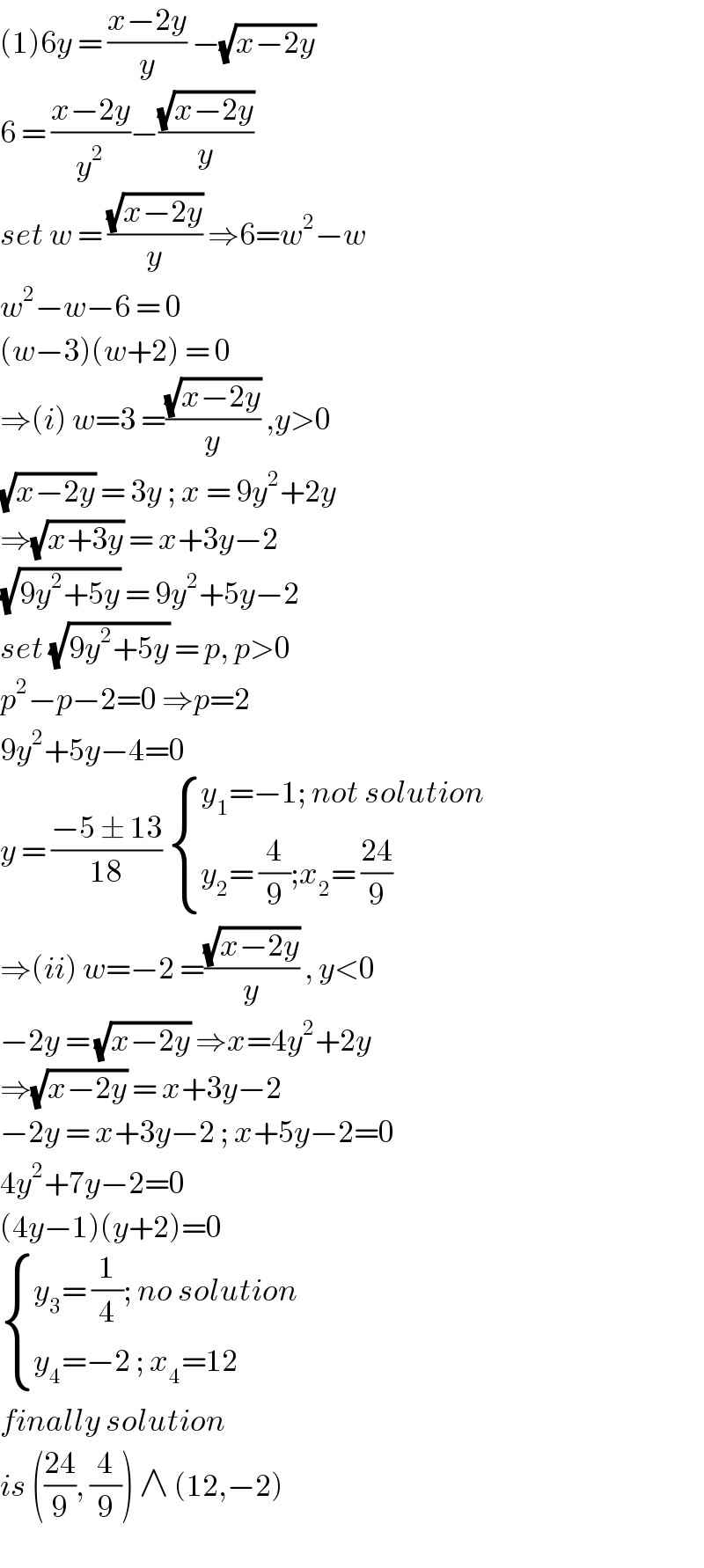
(1)6y = ((x−2y)/y) −(√(x−2y)) 6 = ((x−2y)/y^2 )−((√(x−2y))/y) set w = ((√(x−2y))/y) ⇒6=w^2 −w w^2 −w−6 = 0 (w−3)(w+2) = 0 ⇒(i) w=3 =((√(x−2y))/y) ,y>0 (√(x−2y)) = 3y ; x = 9y^2 +2y ⇒(√(x+3y)) = x+3y−2 (√(9y^2 +5y)) = 9y^2 +5y−2 set (√(9y^2 +5y)) = p, p>0 p^2 −p−2=0 ⇒p=2 9y^2 +5y−4=0 y = ((−5 ± 13)/(18)) { ((y_1 =−1; not solution)),((y_2 = (4/9);x_2 = ((24)/9))) :} ⇒(ii) w=−2 =((√(x−2y))/y) , y<0 −2y = (√(x−2y)) ⇒x=4y^2 +2y ⇒(√(x−2y)) = x+3y−2 −2y = x+3y−2 ; x+5y−2=0 4y^2 +7y−2=0 (4y−1)(y+2)=0 { ((y_3 = (1/4); no solution)),((y_4 =−2 ; x_4 =12 )) :} finally solution is (((24)/9), (4/9)) ∧ (12,−2)
$$\left(\mathrm{1}\right)\mathrm{6}{y}\:=\:\frac{{x}−\mathrm{2}{y}}{{y}}\:−\sqrt{{x}−\mathrm{2}{y}} \\ $$$$\mathrm{6}\:=\:\frac{{x}−\mathrm{2}{y}}{{y}^{\mathrm{2}} }−\frac{\sqrt{{x}−\mathrm{2}{y}}}{{y}}\: \\ $$$${set}\:{w}\:=\:\frac{\sqrt{{x}−\mathrm{2}{y}}}{{y}}\:\Rightarrow\mathrm{6}={w}^{\mathrm{2}} −{w} \\ $$$${w}^{\mathrm{2}} −{w}−\mathrm{6}\:=\:\mathrm{0} \\ $$$$\left({w}−\mathrm{3}\right)\left({w}+\mathrm{2}\right)\:=\:\mathrm{0}\: \\ $$$$\Rightarrow\left({i}\right)\:{w}=\mathrm{3}\:=\frac{\sqrt{{x}−\mathrm{2}{y}}}{{y}}\:,{y}>\mathrm{0} \\ $$$$\sqrt{{x}−\mathrm{2}{y}}\:=\:\mathrm{3}{y}\:;\:{x}\:=\:\mathrm{9}{y}^{\mathrm{2}} +\mathrm{2}{y} \\ $$$$\Rightarrow\sqrt{{x}+\mathrm{3}{y}}\:=\:{x}+\mathrm{3}{y}−\mathrm{2} \\ $$$$\sqrt{\mathrm{9}{y}^{\mathrm{2}} +\mathrm{5}{y}}\:=\:\mathrm{9}{y}^{\mathrm{2}} +\mathrm{5}{y}−\mathrm{2} \\ $$$${set}\:\sqrt{\mathrm{9}{y}^{\mathrm{2}} +\mathrm{5}{y}}\:=\:{p},\:{p}>\mathrm{0} \\ $$$${p}^{\mathrm{2}} −{p}−\mathrm{2}=\mathrm{0}\:\Rightarrow{p}=\mathrm{2} \\ $$$$\mathrm{9}{y}^{\mathrm{2}} +\mathrm{5}{y}−\mathrm{4}=\mathrm{0} \\ $$$${y}\:=\:\frac{−\mathrm{5}\:\pm\:\mathrm{13}}{\mathrm{18}}\:\begin{cases}{{y}_{\mathrm{1}} =−\mathrm{1};\:{not}\:{solution}}\\{{y}_{\mathrm{2}} =\:\frac{\mathrm{4}}{\mathrm{9}};{x}_{\mathrm{2}} =\:\frac{\mathrm{24}}{\mathrm{9}}}\end{cases} \\ $$$$\Rightarrow\left({ii}\right)\:{w}=−\mathrm{2}\:=\frac{\sqrt{{x}−\mathrm{2}{y}}}{{y}}\:,\:{y}<\mathrm{0} \\ $$$$−\mathrm{2}{y}\:=\:\sqrt{{x}−\mathrm{2}{y}}\:\Rightarrow{x}=\mathrm{4}{y}^{\mathrm{2}} +\mathrm{2}{y} \\ $$$$\Rightarrow\sqrt{{x}−\mathrm{2}{y}}\:=\:{x}+\mathrm{3}{y}−\mathrm{2} \\ $$$$−\mathrm{2}{y}\:=\:{x}+\mathrm{3}{y}−\mathrm{2}\:;\:{x}+\mathrm{5}{y}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} +\mathrm{7}{y}−\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{4}{y}−\mathrm{1}\right)\left({y}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\begin{cases}{{y}_{\mathrm{3}} =\:\frac{\mathrm{1}}{\mathrm{4}};\:{no}\:{solution}}\\{{y}_{\mathrm{4}} =−\mathrm{2}\:;\:{x}_{\mathrm{4}} =\mathrm{12}\:}\end{cases} \\ $$$${finally}\:{solution}\: \\ $$$${is}\:\left(\frac{\mathrm{24}}{\mathrm{9}},\:\frac{\mathrm{4}}{\mathrm{9}}\right)\:\wedge\:\left(\mathrm{12},−\mathrm{2}\right)\: \\ $$
Commented by jagoll last updated on 03/May/20
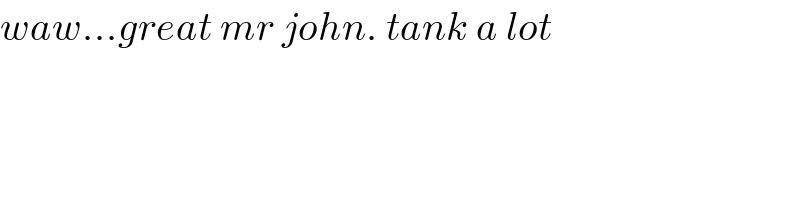
waw...great mr john. tank a lot
$${waw}…{great}\:{mr}\:{john}.\:{tank}\:{a}\:{lot} \\ $$
Commented by niroj last updated on 03/May/20
✔��
Commented by john santu last updated on 03/May/20
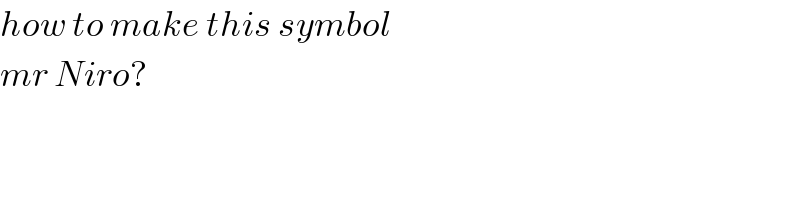
how to make this symbol mr Niro?
$${how}\:{to}\:{make}\:{this}\:{symbol} \\ $$$${mr}\:{Niro}? \\ $$
Commented by niroj last updated on 03/May/20
go to more & tap last option add plaintext comment dear mr.john santu
$$\:\mathrm{go}\:\mathrm{to}\:\mathrm{more}\:\&\:\mathrm{tap}\:\mathrm{last}\:\mathrm{option}\:\mathrm{add}\:\mathrm{plaintext}\:\mathrm{comment} \\ $$$$\:\mathrm{dear}\:\mathrm{mr}.\mathrm{john}\:\mathrm{santu} \\ $$
Commented by jagoll last updated on 03/May/20
good ^o^
Commented by john santu last updated on 03/May/20
������

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *