Question Number 162471 by mr W last updated on 29/Dec/21
![[reposted] find β«_( 0) ^( (π/2)) sin^8 (x)dx + β«_( 0) ^( 1) sin^(-1) ((x)^(1/8) ) dx=?](https://www.tinkutara.com/question/Q162471.png)
$$\left[{reposted}\right] \\ $$$${find}\:\underset{\:\mathrm{0}} {\overset{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\int}}\:\mathrm{sin}^{\mathrm{8}} \left(\mathrm{x}\right){dx}\:+\:\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\mathrm{sin}^{-\mathrm{1}} \left(\sqrt[{\mathrm{8}}]{\mathrm{x}}\right)\:{dx}=? \\ $$
Answered by Ar Brandon last updated on 30/Dec/21
![I=β«_0 ^(Ο/2) sin^8 xdx+β«_0 ^1 sin^(β1) ((x)^(1/8) )dx I_1 =β«_0 ^(Ο/2) sin^8 xdx , I_2 =β«_0 ^1 sin^(β1) ((x)^(1/8) )dx I_2 =β«_0 ^1 sin^(β1) ((x)^(1/8) )dx , x=t^8 βdx=8t^7 dt =8β«_0 ^1 t^7 sin^(β1) (t)dt, { ((u(t)=sin^(β1) (t))),((vβ²(t)=t^7 )) :}β { ((uβ²(t)=(1/( (β(1βt^2 )))))),((v(t)=(1/8)t^8 )) :} =[t^8 sin^(β1) (t)]_0 ^1 ββ«_0 ^1 (t^8 /( (β(1βt^2 ))))dt, t=sinΟβdt=cosΟdΟ =(Ο/2)ββ«^(Ο/2) _0 sin^8 ΟdΟ=(Ο/2)ββ«_0 ^(Ο/2) sin^8 xdx=(Ο/2)βI_1 I=I_1 +I_2 =I_1 +(Ο/2)βI_1 =(Ο/2)](https://www.tinkutara.com/question/Q162474.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{8}} {xdx}+\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}^{β\mathrm{1}} \left(\sqrt[{\mathrm{8}}]{{x}}\right){dx} \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{8}} {xdx}\:,\:{I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}^{β\mathrm{1}} \left(\sqrt[{\mathrm{8}}]{{x}}\right){dx} \\ $$$${I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}^{β\mathrm{1}} \left(\sqrt[{\mathrm{8}}]{{x}}\right){dx}\:,\:{x}={t}^{\mathrm{8}} \Rightarrow{dx}=\mathrm{8}{t}^{\mathrm{7}} {dt} \\ $$$$\:\:\:\:\:=\mathrm{8}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{7}} \mathrm{sin}^{β\mathrm{1}} \left({t}\right){dt},\:\begin{cases}{{u}\left({t}\right)=\mathrm{sin}^{β\mathrm{1}} \left({t}\right)}\\{\mathrm{v}'\left({t}\right)={t}^{\mathrm{7}} }\end{cases}\Rightarrow\begin{cases}{{u}'\left({t}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}β{t}^{\mathrm{2}} }}}\\{\mathrm{v}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{8}}{t}^{\mathrm{8}} }\end{cases} \\ $$$$\:\:\:\:\:=\left[{t}^{\mathrm{8}} \mathrm{sin}^{β\mathrm{1}} \left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} β\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{8}} }{\:\sqrt{\mathrm{1}β{t}^{\mathrm{2}} }}{dt},\:{t}=\mathrm{sin}\vartheta\Rightarrow{dt}=\mathrm{cos}\vartheta{d}\vartheta \\ $$$$\:\:\:\:\:=\frac{\pi}{\mathrm{2}}β\underset{\mathrm{0}} {\int}^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{8}} \vartheta{d}\vartheta=\frac{\pi}{\mathrm{2}}β\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{8}} {xdx}=\frac{\pi}{\mathrm{2}}β{I}_{\mathrm{1}} \\ $$$${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} ={I}_{\mathrm{1}} +\frac{\pi}{\mathrm{2}}β{I}_{\mathrm{1}} =\frac{\pi}{\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 30/Dec/21
$$\mathrm{Thanks}\:\mathrm{Sir}.\:\mathrm{Corrected}\:!\:\mathrm{It}'\mathrm{s}\:\mathrm{okay}\:\mathrm{now}. \\ $$
Commented by Ar Brandon last updated on 29/Dec/21
Commented by Ar Brandon last updated on 29/Dec/21
$$\mathrm{No},\:\mathrm{Sir}. \\ $$
Commented by mr W last updated on 30/Dec/21
$${thanks}\:{for}\:{confirming}\:{sir}! \\ $$
Answered by mr W last updated on 29/Dec/21
$${we}\:{can}\:{solve}\:{this}\:{integral}\:{without} \\ $$$${calculating}\:{it}. \\ $$
Commented by mr W last updated on 29/Dec/21
![we want to find I=I_1 +I_2 with I_1 =β«_0 ^(Ο/2) sin^8 x dx I_2 =β«_0 ^1 sin^(β1) ((x)^(1/8) ) dx now we apply method above to find I_2 =β«_0 ^1 sin^(β1) ((x)^(1/8) )dx y=f(x)=sin^(β1) ((x)^(1/8) ) βx=sin^8 (y)=f^(β1) (y) xβ[0,1] βyβ[0,(Ο/2)] I_2 =β«_0 ^1 sin^(β1) ((x)^(1/8) )dx =1Γ(Ο/2)ββ«_0 ^(Ο/2) sin^8 (y)dy =(Ο/2)ββ«_0 ^(Ο/2) sin^8 (x)dx =(Ο/2)βI_1 I=I_1 +I_2 =I_1 +(Ο/2)βI_1 =(Ο/2) β this works even when we donβ²t know how to calculate the concrete integrals. for the same reason we can get e.g. β«_0 ^(Ο/2) sin^(100) x dx+β«_0 ^1 sin^(β1) ((x)^(1/(100)) ) dx=(Ο/2)](https://www.tinkutara.com/question/Q162501.png)
$${we}\:{want}\:{to}\:{find}\:{I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \:{with}\: \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{8}} \:{x}\:{dx} \\ $$$$\:{I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}^{β\mathrm{1}} \left(\sqrt[{\mathrm{8}}]{{x}}\right)\:{dx} \\ $$$${now}\:{we}\:{apply}\:{method}\:{above}\:{to}\:{find} \\ $$$${I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}^{β\mathrm{1}} \left(\sqrt[{\mathrm{8}}]{{x}}\right){dx} \\ $$$${y}={f}\left({x}\right)=\mathrm{sin}^{β\mathrm{1}} \left(\sqrt[{\mathrm{8}}]{{x}}\right)\: \\ $$$$\Rightarrow{x}=\mathrm{sin}^{\mathrm{8}} \:\left({y}\right)={f}^{β\mathrm{1}} \left({y}\right) \\ $$$${x}\in\left[\mathrm{0},\mathrm{1}\right]\:\Rightarrow{y}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right] \\ $$$${I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}^{β\mathrm{1}} \left(\sqrt[{\mathrm{8}}]{{x}}\right){dx} \\ $$$$\:\:\:\:\:=\mathrm{1}Γ\frac{\pi}{\mathrm{2}}β\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{8}} \:\left({y}\right){dy} \\ $$$$\:\:\:\:\:=\frac{\pi}{\mathrm{2}}β\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{8}} \:\left({x}\right){dx} \\ $$$$\:\:\:\:\:=\frac{\pi}{\mathrm{2}}β{I}_{\mathrm{1}} \\ $$$${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} ={I}_{\mathrm{1}} +\frac{\pi}{\mathrm{2}}β{I}_{\mathrm{1}} =\frac{\pi}{\mathrm{2}}\:\checkmark \\ $$$${this}\:{works}\:{even}\:{when}\:{we}\:{don}'{t}\:{know} \\ $$$${how}\:{to}\:{calculate}\:{the}\:{concrete}\:{integrals}. \\ $$$$ \\ $$$${for}\:{the}\:{same}\:{reason}\:{we}\:{can}\:{get}\:{e}.{g}. \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{100}} \:{x}\:{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}^{β\mathrm{1}} \left(\sqrt[{\mathrm{100}}]{{x}}\right)\:{dx}=\frac{\pi}{\mathrm{2}} \\ $$
Commented by mr W last updated on 29/Dec/21
Commented by mr W last updated on 29/Dec/21
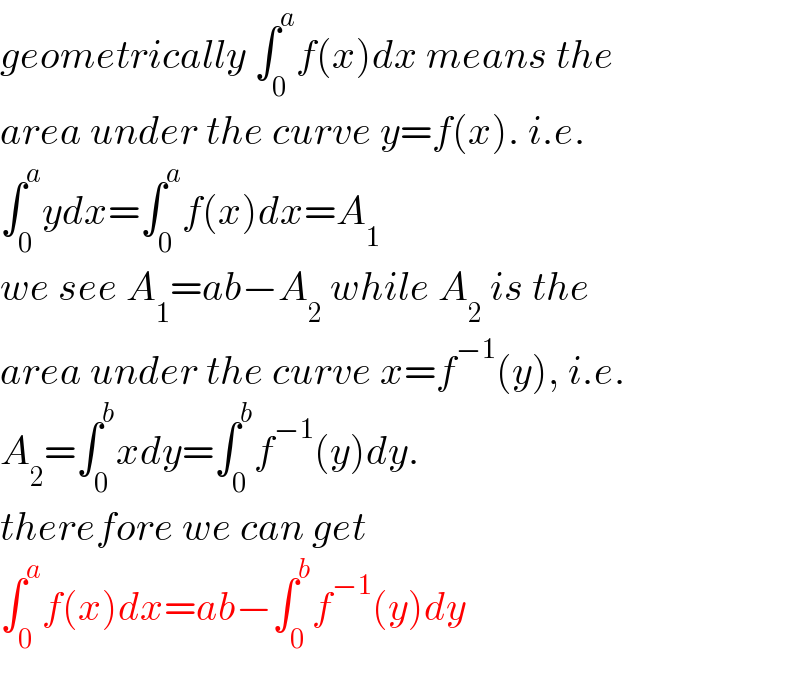
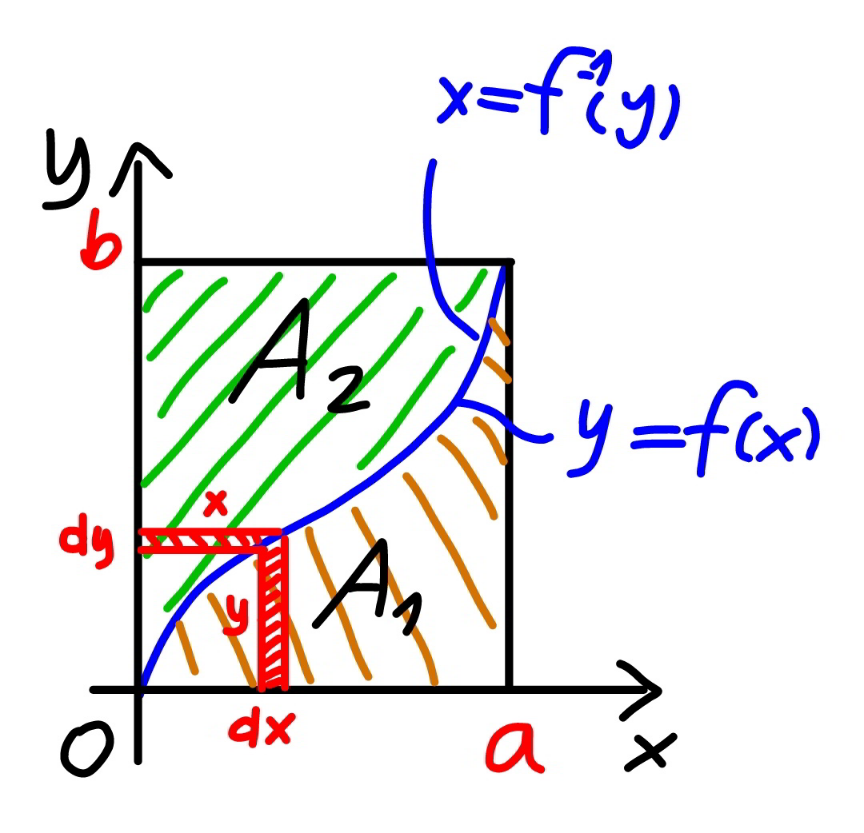
$${geometrically}\:\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}\:{means}\:{the} \\ $$$${area}\:{under}\:{the}\:{curve}\:{y}={f}\left({x}\right).\:{i}.{e}. \\ $$$$\int_{\mathrm{0}} ^{{a}} {ydx}=\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}={A}_{\mathrm{1}} \\ $$$${we}\:{see}\:{A}_{\mathrm{1}} ={ab}β{A}_{\mathrm{2}} \:{while}\:{A}_{\mathrm{2}} \:{is}\:{the} \\ $$$${area}\:{under}\:{the}\:{curve}\:{x}={f}^{β\mathrm{1}} \left({y}\right),\:{i}.{e}. \\ $$$${A}_{\mathrm{2}} =\int_{\mathrm{0}} ^{{b}} {xdy}=\int_{\mathrm{0}} ^{{b}} {f}^{β\mathrm{1}} \left({y}\right){dy}. \\ $$$${therefore}\:{we}\:{can}\:{get} \\ $$$$\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}={ab}β\int_{\mathrm{0}} ^{{b}} {f}^{β\mathrm{1}} \left({y}\right){dy} \\ $$
Commented by Tawa11 last updated on 30/Dec/21
$$\mathrm{Wow}\:\mathrm{great}\:\mathrm{sir}. \\ $$