Menu Close

reposting-this-x-8-8x-7-16x-6-208x-5-152x-4-928x-3-704x-2-1088x-368-0-nobody-wants-to-try-it-s-beautiful-

Tinku Tara 0 Comments
Pin




Question Number 58915 by MJS last updated on 01/May/19
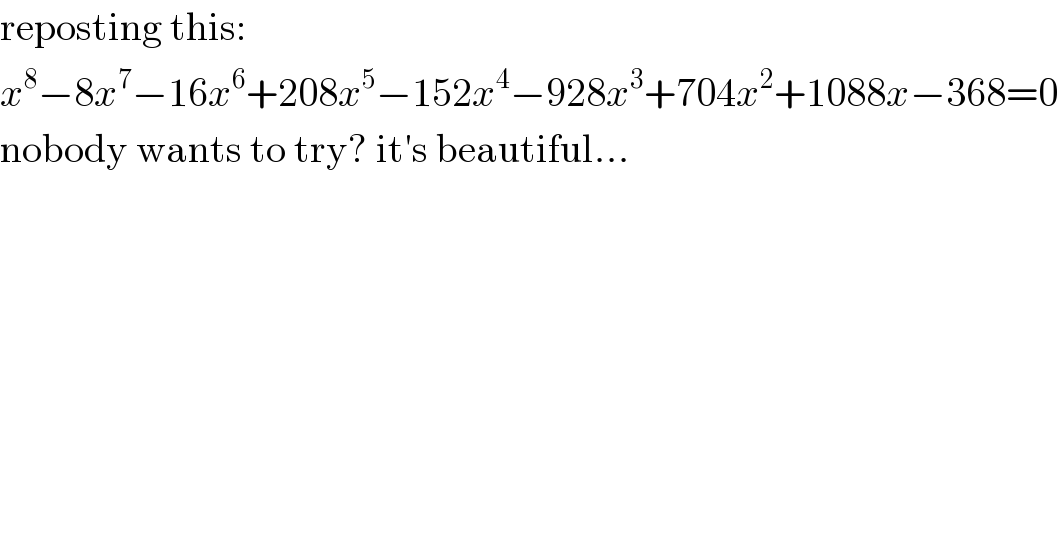
reposting this: x^8 −8x^7 −16x^6 +208x^5 −152x^4 −928x^3 +704x^2 +1088x−368=0 nobody wants to try? it′s beautiful...
$$\mathrm{reposting}\:\mathrm{this}: \\ $$$${x}^{\mathrm{8}} −\mathrm{8}{x}^{\mathrm{7}} −\mathrm{16}{x}^{\mathrm{6}} +\mathrm{208}{x}^{\mathrm{5}} −\mathrm{152}{x}^{\mathrm{4}} −\mathrm{928}{x}^{\mathrm{3}} +\mathrm{704}{x}^{\mathrm{2}} +\mathrm{1088}{x}−\mathrm{368}=\mathrm{0} \\ $$$$\mathrm{nobody}\:\mathrm{wants}\:\mathrm{to}\:\mathrm{try}?\:\mathrm{it}'\mathrm{s}\:\mathrm{beautiful}… \\ $$
Commented by Kunal12588 last updated on 01/May/19
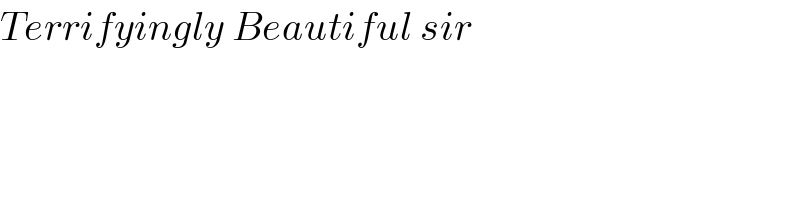
Terrifyingly Beautiful sir
$${Terrifyingly}\:{Beautiful}\:{sir} \\ $$
Commented by Kunal12588 last updated on 01/May/19
Answered by naka3546 last updated on 01/May/19
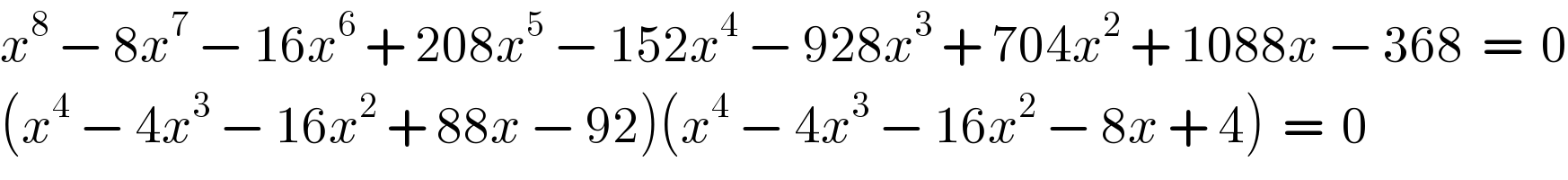
x^8 − 8x^7 − 16x^6 + 208x^5 − 152x^4 − 928x^3 + 704x^2 + 1088x − 368 = 0 (x^4 − 4x^3 − 16x^2 + 88x − 92)(x^4 − 4x^3 − 16x^2 − 8x + 4) = 0
$${x}^{\mathrm{8}} \:−\:\mathrm{8}{x}^{\mathrm{7}} \:−\:\mathrm{16}{x}^{\mathrm{6}} \:+\:\mathrm{208}{x}^{\mathrm{5}} \:−\:\mathrm{152}{x}^{\mathrm{4}} \:−\:\mathrm{928}{x}^{\mathrm{3}} \:+\:\mathrm{704}{x}^{\mathrm{2}} \:+\:\mathrm{1088}{x}\:−\:\mathrm{368}\:\:=\:\:\mathrm{0} \\ $$$$\left({x}^{\mathrm{4}} \:−\:\mathrm{4}{x}^{\mathrm{3}} \:−\:\mathrm{16}{x}^{\mathrm{2}} \:+\:\mathrm{88}{x}\:−\:\mathrm{92}\right)\left({x}^{\mathrm{4}} \:−\:\mathrm{4}{x}^{\mathrm{3}} \:−\:\mathrm{16}{x}^{\mathrm{2}} \:−\:\mathrm{8}{x}\:+\:\mathrm{4}\right)\:\:=\:\:\mathrm{0} \\ $$
Commented by naka3546 last updated on 01/May/19
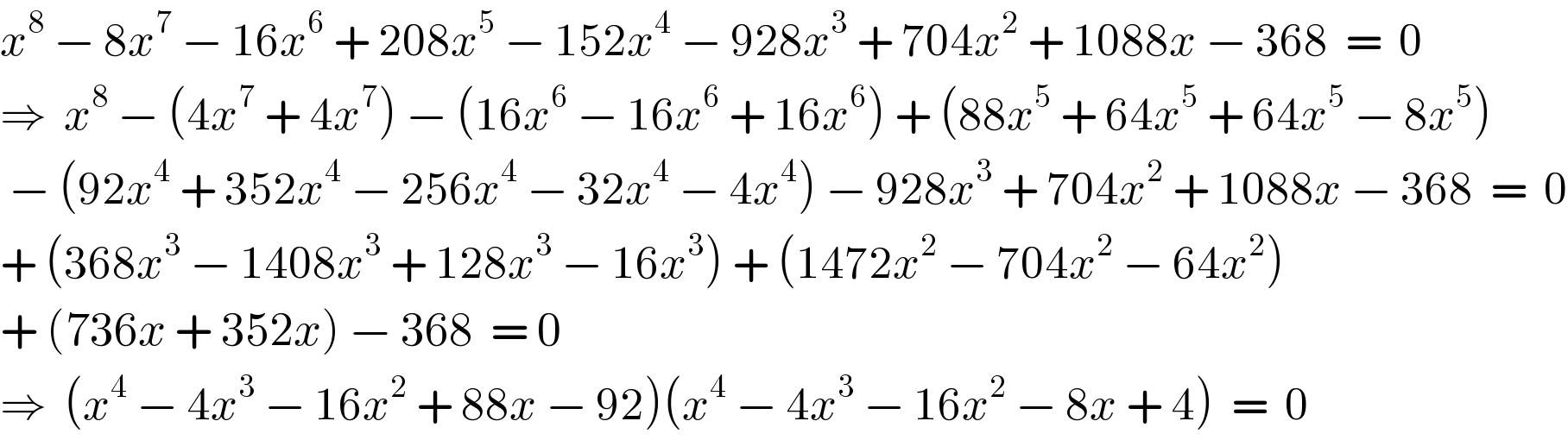
x^8 − 8x^7 − 16x^6 + 208x^5 − 152x^4 − 928x^3 + 704x^2 + 1088x − 368 = 0 ⇒ x^8 − (4x^7 + 4x^7 ) − (16x^6 − 16x^6 + 16x^6 ) + (88x^5 + 64x^5 + 64x^5 − 8x^5 ) − (92x^4 + 352x^4 − 256x^4 − 32x^4 − 4x^4 ) − 928x^3 + 704x^2 + 1088x − 368 = 0 + (368x^3 − 1408x^3 + 128x^3 − 16x^3 ) + (1472x^2 − 704x^2 − 64x^2 ) + (736x + 352x) − 368 = 0 ⇒ (x^4 − 4x^3 − 16x^2 + 88x − 92)(x^4 − 4x^3 − 16x^2 − 8x + 4) = 0
$${x}^{\mathrm{8}} \:−\:\mathrm{8}{x}^{\mathrm{7}} \:−\:\mathrm{16}{x}^{\mathrm{6}} \:+\:\mathrm{208}{x}^{\mathrm{5}} \:−\:\mathrm{152}{x}^{\mathrm{4}} \:−\:\mathrm{928}{x}^{\mathrm{3}} \:+\:\mathrm{704}{x}^{\mathrm{2}} \:+\:\mathrm{1088}{x}\:−\:\mathrm{368}\:\:=\:\:\mathrm{0} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{8}} \:−\:\left(\mathrm{4}{x}^{\mathrm{7}} \:+\:\mathrm{4}{x}^{\mathrm{7}} \right)\:−\:\left(\mathrm{16}{x}^{\mathrm{6}} \:−\:\mathrm{16}{x}^{\mathrm{6}} \:+\:\mathrm{16}{x}^{\mathrm{6}} \right)\:+\:\left(\mathrm{88}{x}^{\mathrm{5}} \:+\:\mathrm{64}{x}^{\mathrm{5}} \:+\:\mathrm{64}{x}^{\mathrm{5}} \:−\:\mathrm{8}{x}^{\mathrm{5}} \right) \\ $$$$\:−\:\left(\mathrm{92}{x}^{\mathrm{4}} \:+\:\mathrm{352}{x}^{\mathrm{4}} \:−\:\mathrm{256}{x}^{\mathrm{4}} \:−\:\mathrm{32}{x}^{\mathrm{4}} \:−\:\mathrm{4}{x}^{\mathrm{4}} \right)\:−\:\mathrm{928}{x}^{\mathrm{3}} \:+\:\mathrm{704}{x}^{\mathrm{2}} \:+\:\mathrm{1088}{x}\:−\:\mathrm{368}\:\:=\:\:\mathrm{0} \\ $$$$+\:\left(\mathrm{368}{x}^{\mathrm{3}} \:−\:\mathrm{1408}{x}^{\mathrm{3}} \:+\:\mathrm{128}{x}^{\mathrm{3}} \:−\:\mathrm{16}{x}^{\mathrm{3}} \right)\:+\:\left(\mathrm{1472}{x}^{\mathrm{2}} \:−\:\mathrm{704}{x}^{\mathrm{2}} \:−\:\mathrm{64}{x}^{\mathrm{2}} \right) \\ $$$$+\:\left(\mathrm{736}{x}\:+\:\mathrm{352}{x}\right)\:−\:\mathrm{368}\:\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\left({x}^{\mathrm{4}} \:−\:\mathrm{4}{x}^{\mathrm{3}} \:−\:\mathrm{16}{x}^{\mathrm{2}} \:+\:\mathrm{88}{x}\:−\:\mathrm{92}\right)\left({x}^{\mathrm{4}} \:−\:\mathrm{4}{x}^{\mathrm{3}} \:−\:\mathrm{16}{x}^{\mathrm{2}} \:−\:\mathrm{8}{x}\:+\:\mathrm{4}\right)\:\:=\:\:\mathrm{0} \\ $$
Commented by MJS last updated on 01/May/19
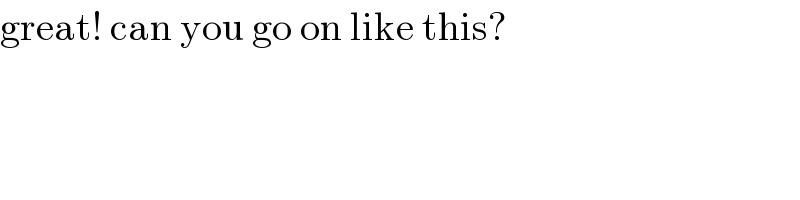
great! can you go on like this?
$$\mathrm{great}!\:\mathrm{can}\:\mathrm{you}\:\mathrm{go}\:\mathrm{on}\:\mathrm{like}\:\mathrm{this}? \\ $$
Answered by MJS last updated on 01/May/19
x=w+1 w^8 −44w^6 +438w^4 −1292w^2 +529=0 w=±(√v) v^4 −44v^3 +438v^2 −1292v+529=0 v_(1, 2) =α±(√β) v_(3, 4) =γ±(√δ) (v−v_1 )(v−v_2 )(v−v_3 )(v−v_4 )=v^4 −44v^3 +438v^2 −1292v+529 −2α−2γ=−44 ⇒ α=−γ+22 α^2 +4αγ−β+γ^2 −δ=438 ⇒ β=−2γ^2 +44γ−δ+46 −2α^2 γ−2αγ^2 +2αδ+2βγ=−1292 ⇒ δ=((−γ^3 +33γ^2 −219γ+323)/(γ−11)) α^2 γ^2 −α^2 δ−βγ^2 +βδ=529 ⇒ ⇒ γ^6 −66γ^5 +1671γ^4 −20284γ^3 +121407γ^2 −339042γ+346969=0 γ=u+11 u^6 −144u^4 +6336u^2 −82944=0 u=(√t) t^3 −144t^2 +6336t−82944=0 t=s+48 s^3 −576s=0 ⇒ s_1 =−24; s_2 =0; s_3 =24 s=0 t=48 u=4(√3) γ=11+4(√3) δ=96+48(√3) (√δ)=6(√2)+2(√6) α=11−4(√3) β=96−48(√3) (√β)=6(√2)−2(√6) v_1 =11−6(√2)−4(√3)+2(√6) v_2 =11+6(√2)−4(√3)−2(√6) v_3 =11−6(√2)+4(√3)−2(√6) v_4 =11+6(√2)+4(√3)+2(√6) w_(1, 2) =±(√v_1 ) w_(3, 4) =±(√v_2 ) w_(5, 6) =±(√v_3 ) w_(7, 8) =±(√v_4 ) (√v_4 )=(√(11+6(√2)+4(√3)+2(√6)))=a+b(√2)+c(√3)+d(√6) 11+6(√2)+4(√3)+2(√6)=(a^2 +2b^2 +3c^2 +6d^2 )o+2(ab+3cd)(√2)+2(ac+3bd)(√3)+2(ad+bc)(√6) now an obvious solution is a=0∧b=c=d=1 ⇒ (√v_4 )=(√(11+6(√2)+4(√3)+2(√6)))=(√2)+(√3)+(√6) similar (√v_1 )=(√2)+(√3)−(√6) (√v_2 )=−(√2)+(√3)+(√6) (√v_3 )=(√2)−(√3)+(√6) w_1 =−(√2)−(√3)+(√6) ⇒ x_1 =1−(√2)−(√3)+(√6) w_2 =(√2)+(√3)−(√6) ⇒ x_2 =1+(√2)+(√3)−(√6) w_3 =(√2)−(√3)−(√6) ⇒ x_3 =1+(√2)−(√3)−(√6) w_4 =−(√2)+(√3)+(√6) ⇒ x_4 =1−(√2)+(√3)+(√6) w_5 =−(√2)+(√3)−(√6) ⇒ x_5 =1−(√2)+(√3)−(√6) w_6 =(√2)−(√3)+(√6) ⇒ x_6 =1+(√2)−(√3)+(√6) w_7 =−(√2)−(√3)−(√6) ⇒ x_7 =1−(√2)−(√3)−(√6) w_8 =(√2)+(√3)+(√6) ⇒ x_8 =1+(√2)+(√3)+(√6)
$${x}={w}+\mathrm{1} \\ $$$${w}^{\mathrm{8}} −\mathrm{44}{w}^{\mathrm{6}} +\mathrm{438}{w}^{\mathrm{4}} −\mathrm{1292}{w}^{\mathrm{2}} +\mathrm{529}=\mathrm{0} \\ $$$${w}=\pm\sqrt{{v}} \\ $$$${v}^{\mathrm{4}} −\mathrm{44}{v}^{\mathrm{3}} +\mathrm{438}{v}^{\mathrm{2}} −\mathrm{1292}{v}+\mathrm{529}=\mathrm{0} \\ $$$${v}_{\mathrm{1},\:\mathrm{2}} =\alpha\pm\sqrt{\beta} \\ $$$${v}_{\mathrm{3},\:\mathrm{4}} =\gamma\pm\sqrt{\delta} \\ $$$$\left({v}−{v}_{\mathrm{1}} \right)\left({v}−{v}_{\mathrm{2}} \right)\left({v}−{v}_{\mathrm{3}} \right)\left({v}−{v}_{\mathrm{4}} \right)={v}^{\mathrm{4}} −\mathrm{44}{v}^{\mathrm{3}} +\mathrm{438}{v}^{\mathrm{2}} −\mathrm{1292}{v}+\mathrm{529} \\ $$$$−\mathrm{2}\alpha−\mathrm{2}\gamma=−\mathrm{44}\:\Rightarrow\:\alpha=−\gamma+\mathrm{22} \\ $$$$\alpha^{\mathrm{2}} +\mathrm{4}\alpha\gamma−\beta+\gamma^{\mathrm{2}} −\delta=\mathrm{438}\:\Rightarrow\:\beta=−\mathrm{2}\gamma^{\mathrm{2}} +\mathrm{44}\gamma−\delta+\mathrm{46} \\ $$$$−\mathrm{2}\alpha^{\mathrm{2}} \gamma−\mathrm{2}\alpha\gamma^{\mathrm{2}} +\mathrm{2}\alpha\delta+\mathrm{2}\beta\gamma=−\mathrm{1292}\:\Rightarrow\:\delta=\frac{−\gamma^{\mathrm{3}} +\mathrm{33}\gamma^{\mathrm{2}} −\mathrm{219}\gamma+\mathrm{323}}{\gamma−\mathrm{11}} \\ $$$$\alpha^{\mathrm{2}} \gamma^{\mathrm{2}} −\alpha^{\mathrm{2}} \delta−\beta\gamma^{\mathrm{2}} +\beta\delta=\mathrm{529}\:\Rightarrow \\ $$$$\Rightarrow\:\gamma^{\mathrm{6}} −\mathrm{66}\gamma^{\mathrm{5}} +\mathrm{1671}\gamma^{\mathrm{4}} −\mathrm{20284}\gamma^{\mathrm{3}} +\mathrm{121407}\gamma^{\mathrm{2}} −\mathrm{339042}\gamma+\mathrm{346969}=\mathrm{0} \\ $$$$\gamma={u}+\mathrm{11} \\ $$$${u}^{\mathrm{6}} −\mathrm{144}{u}^{\mathrm{4}} +\mathrm{6336}{u}^{\mathrm{2}} −\mathrm{82944}=\mathrm{0} \\ $$$${u}=\sqrt{{t}} \\ $$$${t}^{\mathrm{3}} −\mathrm{144}{t}^{\mathrm{2}} +\mathrm{6336}{t}−\mathrm{82944}=\mathrm{0} \\ $$$${t}={s}+\mathrm{48} \\ $$$${s}^{\mathrm{3}} −\mathrm{576}{s}=\mathrm{0}\:\Rightarrow\:{s}_{\mathrm{1}} =−\mathrm{24};\:{s}_{\mathrm{2}} =\mathrm{0};\:{s}_{\mathrm{3}} =\mathrm{24} \\ $$$${s}=\mathrm{0} \\ $$$${t}=\mathrm{48} \\ $$$${u}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$\gamma=\mathrm{11}+\mathrm{4}\sqrt{\mathrm{3}}\:\:\delta=\mathrm{96}+\mathrm{48}\sqrt{\mathrm{3}}\:\:\sqrt{\delta}=\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\alpha=\mathrm{11}−\mathrm{4}\sqrt{\mathrm{3}}\:\:\beta=\mathrm{96}−\mathrm{48}\sqrt{\mathrm{3}}\:\:\sqrt{\beta}=\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{6}} \\ $$$${v}_{\mathrm{1}} =\mathrm{11}−\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{6}} \\ $$$${v}_{\mathrm{2}} =\mathrm{11}+\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{6}} \\ $$$${v}_{\mathrm{3}} =\mathrm{11}−\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{6}} \\ $$$${v}_{\mathrm{4}} =\mathrm{11}+\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{6}} \\ $$$${w}_{\mathrm{1},\:\mathrm{2}} =\pm\sqrt{{v}_{\mathrm{1}} } \\ $$$${w}_{\mathrm{3},\:\mathrm{4}} =\pm\sqrt{{v}_{\mathrm{2}} } \\ $$$${w}_{\mathrm{5},\:\mathrm{6}} =\pm\sqrt{{v}_{\mathrm{3}} } \\ $$$${w}_{\mathrm{7},\:\mathrm{8}} =\pm\sqrt{{v}_{\mathrm{4}} } \\ $$$$\sqrt{{v}_{\mathrm{4}} }=\sqrt{\mathrm{11}+\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{6}}}={a}+{b}\sqrt{\mathrm{2}}+{c}\sqrt{\mathrm{3}}+{d}\sqrt{\mathrm{6}} \\ $$$$\mathrm{11}+\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{6}}=\left({a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{2}} +\mathrm{6}{d}^{\mathrm{2}} \right){o}+\mathrm{2}\left({ab}+\mathrm{3}{cd}\right)\sqrt{\mathrm{2}}+\mathrm{2}\left({ac}+\mathrm{3}{bd}\right)\sqrt{\mathrm{3}}+\mathrm{2}\left({ad}+{bc}\right)\sqrt{\mathrm{6}} \\ $$$$\mathrm{now}\:\mathrm{an}\:\mathrm{obvious}\:\mathrm{solution}\:\mathrm{is}\:{a}=\mathrm{0}\wedge{b}={c}={d}=\mathrm{1} \\ $$$$\Rightarrow\:\sqrt{{v}_{\mathrm{4}} }=\sqrt{\mathrm{11}+\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{6}}}=\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}} \\ $$$$\mathrm{similar} \\ $$$$\sqrt{{v}_{\mathrm{1}} }=\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{6}} \\ $$$$\sqrt{{v}_{\mathrm{2}} }=−\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}} \\ $$$$\sqrt{{v}_{\mathrm{3}} }=\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}} \\ $$$${w}_{\mathrm{1}} =−\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}}\:\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{1}−\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}} \\ $$$${w}_{\mathrm{2}} =\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{6}}\:\Rightarrow\:{x}_{\mathrm{2}} =\mathrm{1}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{6}} \\ $$$${w}_{\mathrm{3}} =\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}−\sqrt{\mathrm{6}}\:\Rightarrow\:{x}_{\mathrm{3}} =\mathrm{1}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}−\sqrt{\mathrm{6}} \\ $$$${w}_{\mathrm{4}} =−\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}}\:\Rightarrow\:{x}_{\mathrm{4}} =\mathrm{1}−\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}} \\ $$$${w}_{\mathrm{5}} =−\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{6}}\:\Rightarrow\:{x}_{\mathrm{5}} =\mathrm{1}−\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{6}} \\ $$$${w}_{\mathrm{6}} =\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}}\:\Rightarrow\:{x}_{\mathrm{6}} =\mathrm{1}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}} \\ $$$${w}_{\mathrm{7}} =−\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}−\sqrt{\mathrm{6}}\:\Rightarrow\:{x}_{\mathrm{7}} =\mathrm{1}−\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}−\sqrt{\mathrm{6}} \\ $$$${w}_{\mathrm{8}} =\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}}\:\Rightarrow\:{x}_{\mathrm{8}} =\mathrm{1}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}} \\ $$
Commented by Kunal12588 last updated on 01/May/19
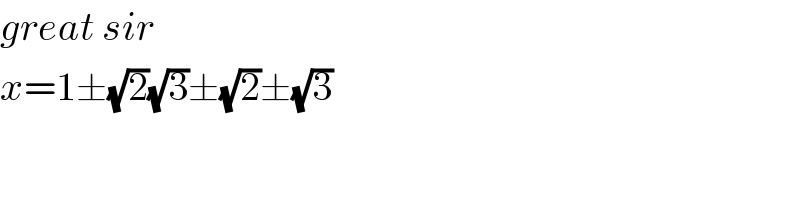
great sir x=1±(√2)(√3)±(√2)±(√3)
$${great}\:{sir} \\ $$$${x}=\mathrm{1}\pm\sqrt{\mathrm{2}}\sqrt{\mathrm{3}}\pm\sqrt{\mathrm{2}}\pm\sqrt{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *