Menu Close

Resolve-1-u-n-2-2u-n-1-4u-n-3-n-with-u-o-1-u-1-2-2-u-n-u-n-1-u-n-2-2sin-n-3-with-u-o-1-u-1-2-

Tinku Tara 0 Comments
Pin




Question Number 159560 by LEKOUMA last updated on 18/Nov/21
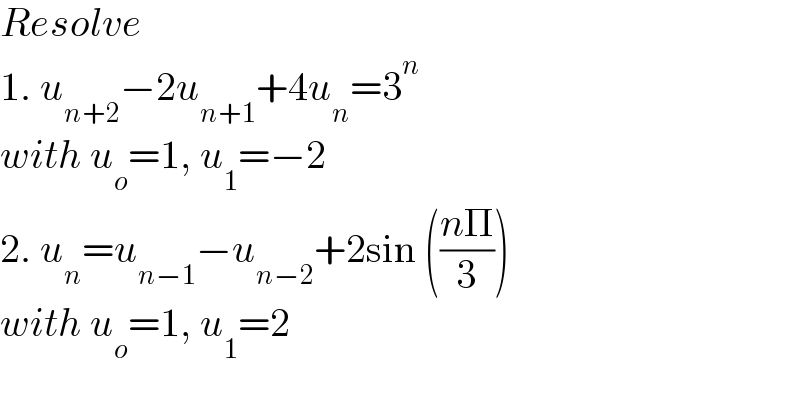
Resolve 1. u_(n+2) −2u_(n+1) +4u_n =3^n with u_o =1, u_1 =−2 2. u_n =u_(n−1) −u_(n−2) +2sin (((nΠ)/3)) with u_o =1, u_1 =2
$${Resolve}\: \\ $$$$\mathrm{1}.\:{u}_{{n}+\mathrm{2}} −\mathrm{2}{u}_{{n}+\mathrm{1}} +\mathrm{4}{u}_{{n}} =\mathrm{3}^{{n}} \\ $$$${with}\:{u}_{{o}} =\mathrm{1},\:{u}_{\mathrm{1}} =−\mathrm{2} \\ $$$$\mathrm{2}.\:{u}_{{n}} ={u}_{{n}−\mathrm{1}} −{u}_{{n}−\mathrm{2}} +\mathrm{2sin}\:\left(\frac{{n}\Pi}{\mathrm{3}}\right) \\ $$$${with}\:{u}_{{o}} =\mathrm{1},\:{u}_{\mathrm{1}} =\mathrm{2} \\ $$
Answered by mr W last updated on 02/Dec/21
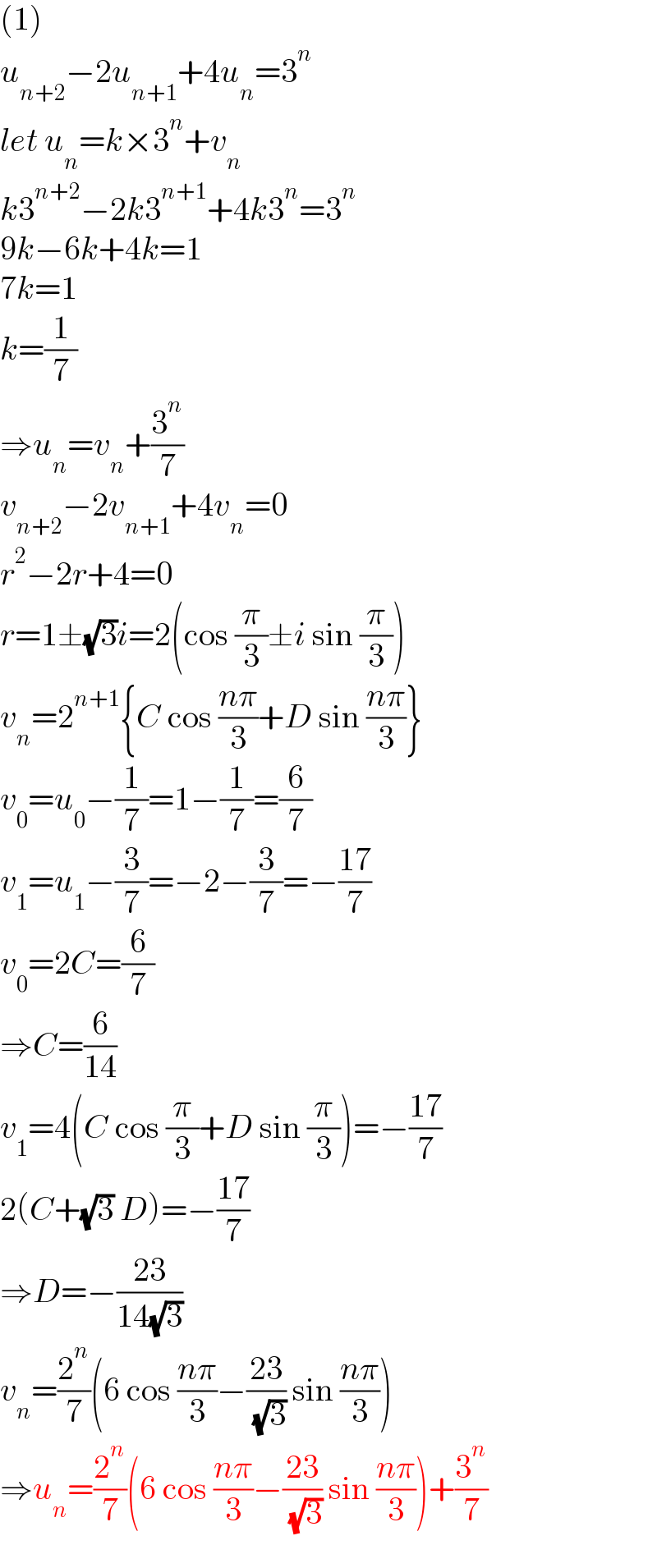
(1) u_(n+2) −2u_(n+1) +4u_n =3^n let u_n =k×3^n +v_n k3^(n+2) −2k3^(n+1) +4k3^n =3^n 9k−6k+4k=1 7k=1 k=(1/7) ⇒u_n =v_n +(3^n /7) v_(n+2) −2v_(n+1) +4v_n =0 r^2 −2r+4=0 r=1±(√3)i=2(cos (π/3)±i sin (π/3)) v_n =2^(n+1) {C cos ((nπ)/3)+D sin ((nπ)/3)} v_0 =u_0 −(1/7)=1−(1/7)=(6/7) v_1 =u_1 −(3/7)=−2−(3/7)=−((17)/7) v_0 =2C=(6/7) ⇒C=(6/(14)) v_1 =4(C cos (π/3)+D sin (π/3))=−((17)/7) 2(C+(√3) D)=−((17)/7) ⇒D=−((23)/(14(√3))) v_n =(2^n /7)(6 cos ((nπ)/3)−((23)/( (√3))) sin ((nπ)/3)) ⇒u_n =(2^n /7)(6 cos ((nπ)/3)−((23)/( (√3))) sin ((nπ)/3))+(3^n /7)
$$\left(\mathrm{1}\right) \\ $$$${u}_{{n}+\mathrm{2}} −\mathrm{2}{u}_{{n}+\mathrm{1}} +\mathrm{4}{u}_{{n}} =\mathrm{3}^{{n}} \\ $$$${let}\:{u}_{{n}} ={k}×\mathrm{3}^{{n}} +{v}_{{n}} \\ $$$${k}\mathrm{3}^{{n}+\mathrm{2}} −\mathrm{2}{k}\mathrm{3}^{{n}+\mathrm{1}} +\mathrm{4}{k}\mathrm{3}^{{n}} =\mathrm{3}^{{n}} \\ $$$$\mathrm{9}{k}−\mathrm{6}{k}+\mathrm{4}{k}=\mathrm{1} \\ $$$$\mathrm{7}{k}=\mathrm{1} \\ $$$${k}=\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\Rightarrow{u}_{{n}} ={v}_{{n}} +\frac{\mathrm{3}^{{n}} }{\mathrm{7}} \\ $$$${v}_{{n}+\mathrm{2}} −\mathrm{2}{v}_{{n}+\mathrm{1}} +\mathrm{4}{v}_{{n}} =\mathrm{0} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{r}+\mathrm{4}=\mathrm{0} \\ $$$${r}=\mathrm{1}\pm\sqrt{\mathrm{3}}{i}=\mathrm{2}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\pm{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\right) \\ $$$${v}_{{n}} =\mathrm{2}^{{n}+\mathrm{1}} \left\{{C}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}}+{D}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}}\right\} \\ $$$${v}_{\mathrm{0}} ={u}_{\mathrm{0}} −\frac{\mathrm{1}}{\mathrm{7}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{7}}=\frac{\mathrm{6}}{\mathrm{7}} \\ $$$${v}_{\mathrm{1}} ={u}_{\mathrm{1}} −\frac{\mathrm{3}}{\mathrm{7}}=−\mathrm{2}−\frac{\mathrm{3}}{\mathrm{7}}=−\frac{\mathrm{17}}{\mathrm{7}} \\ $$$${v}_{\mathrm{0}} =\mathrm{2}{C}=\frac{\mathrm{6}}{\mathrm{7}} \\ $$$$\Rightarrow{C}=\frac{\mathrm{6}}{\mathrm{14}} \\ $$$${v}_{\mathrm{1}} =\mathrm{4}\left({C}\:\mathrm{cos}\:\frac{\pi}{\mathrm{3}}+{D}\:\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\right)=−\frac{\mathrm{17}}{\mathrm{7}} \\ $$$$\mathrm{2}\left({C}+\sqrt{\mathrm{3}}\:{D}\right)=−\frac{\mathrm{17}}{\mathrm{7}} \\ $$$$\Rightarrow{D}=−\frac{\mathrm{23}}{\mathrm{14}\sqrt{\mathrm{3}}} \\ $$$${v}_{{n}} =\frac{\mathrm{2}^{{n}} }{\mathrm{7}}\left(\mathrm{6}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}}−\frac{\mathrm{23}}{\:\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow{u}_{{n}} =\frac{\mathrm{2}^{{n}} }{\mathrm{7}}\left(\mathrm{6}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}}−\frac{\mathrm{23}}{\:\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}}\right)+\frac{\mathrm{3}^{{n}} }{\mathrm{7}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *