Menu Close

Resolve-u-n-3u-n-1-12-3-4-n-and-u-n-2u-n-1-5cos-n-3-u-o-1-

Tinku Tara 0 Comments
Pin




Question Number 160529 by LEKOUMA last updated on 01/Dec/21
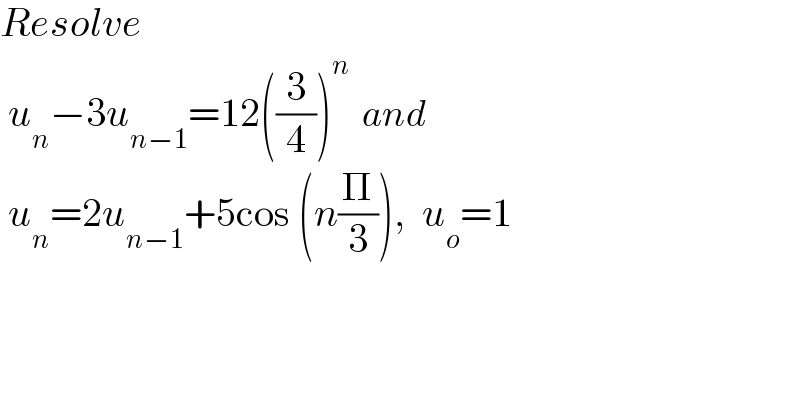
Resolve u_n −3u_(n−1) =12((3/4))^n and u_n =2u_(n−1) +5cos (n(Π/3)), u_o =1
$${Resolve}\: \\ $$$$\:{u}_{{n}} −\mathrm{3}{u}_{{n}−\mathrm{1}} =\mathrm{12}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} \:\:{and} \\ $$$$\:{u}_{{n}} =\mathrm{2}{u}_{{n}−\mathrm{1}} +\mathrm{5cos}\:\left({n}\frac{\Pi}{\mathrm{3}}\right),\:\:{u}_{{o}} =\mathrm{1} \\ $$
Answered by mr W last updated on 02/Dec/21
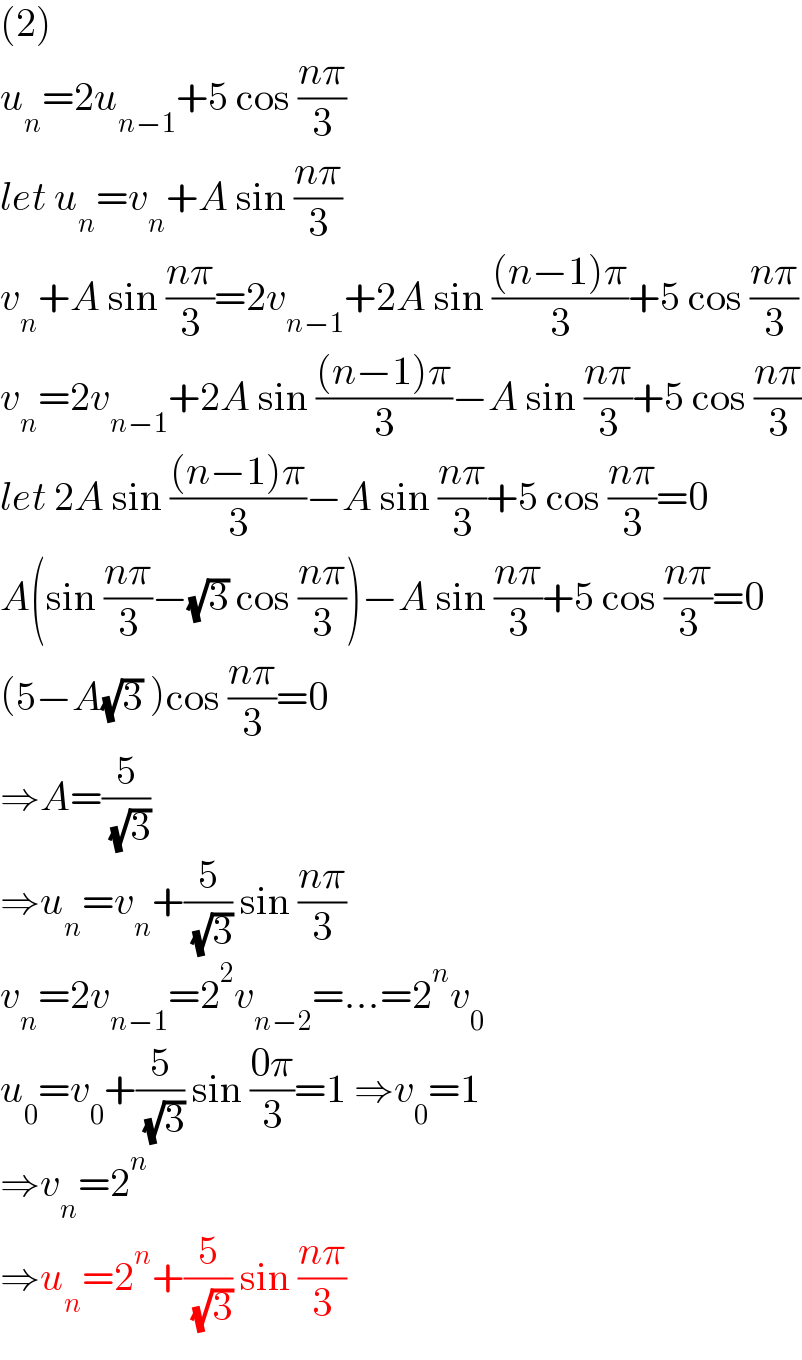
(2) u_n =2u_(n−1) +5 cos ((nπ)/3) let u_n =v_n +A sin ((nπ)/3) v_n +A sin ((nπ)/3)=2v_(n−1) +2A sin (((n−1)π)/3)+5 cos ((nπ)/3) v_n =2v_(n−1) +2A sin (((n−1)π)/3)−A sin ((nπ)/3)+5 cos ((nπ)/3) let 2A sin (((n−1)π)/3)−A sin ((nπ)/3)+5 cos ((nπ)/3)=0 A(sin ((nπ)/3)−(√3) cos ((nπ)/3))−A sin ((nπ)/3)+5 cos ((nπ)/3)=0 (5−A(√3) )cos ((nπ)/3)=0 ⇒A=(5/( (√3))) ⇒u_n =v_n +(5/( (√3))) sin ((nπ)/3) v_n =2v_(n−1) =2^2 v_(n−2) =...=2^n v_0 u_0 =v_0 +(5/( (√3))) sin ((0π)/3)=1 ⇒v_0 =1 ⇒v_n =2^n ⇒u_n =2^n +(5/( (√3))) sin ((nπ)/3)
$$\left(\mathrm{2}\right) \\ $$$${u}_{{n}} =\mathrm{2}{u}_{{n}−\mathrm{1}} +\mathrm{5}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}} \\ $$$${let}\:{u}_{{n}} ={v}_{{n}} +{A}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}} \\ $$$${v}_{{n}} +{A}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}}=\mathrm{2}{v}_{{n}−\mathrm{1}} +\mathrm{2}{A}\:\mathrm{sin}\:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{3}}+\mathrm{5}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}} \\ $$$${v}_{{n}} =\mathrm{2}{v}_{{n}−\mathrm{1}} +\mathrm{2}{A}\:\mathrm{sin}\:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{3}}−{A}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}}+\mathrm{5}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}} \\ $$$${let}\:\mathrm{2}{A}\:\mathrm{sin}\:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{3}}−{A}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}}+\mathrm{5}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}}=\mathrm{0} \\ $$$${A}\left(\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}}−\sqrt{\mathrm{3}}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}}\right)−{A}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}}+\mathrm{5}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}}=\mathrm{0} \\ $$$$\left(\mathrm{5}−{A}\sqrt{\mathrm{3}}\:\right)\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow{A}=\frac{\mathrm{5}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{u}_{{n}} ={v}_{{n}} +\frac{\mathrm{5}}{\:\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}} \\ $$$${v}_{{n}} =\mathrm{2}{v}_{{n}−\mathrm{1}} =\mathrm{2}^{\mathrm{2}} {v}_{{n}−\mathrm{2}} =…=\mathrm{2}^{{n}} {v}_{\mathrm{0}} \\ $$$${u}_{\mathrm{0}} ={v}_{\mathrm{0}} +\frac{\mathrm{5}}{\:\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\frac{\mathrm{0}\pi}{\mathrm{3}}=\mathrm{1}\:\Rightarrow{v}_{\mathrm{0}} =\mathrm{1} \\ $$$$\Rightarrow{v}_{{n}} =\mathrm{2}^{{n}} \\ $$$$\Rightarrow{u}_{{n}} =\mathrm{2}^{{n}} +\frac{\mathrm{5}}{\:\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}} \\ $$
Answered by mr W last updated on 01/Dec/21
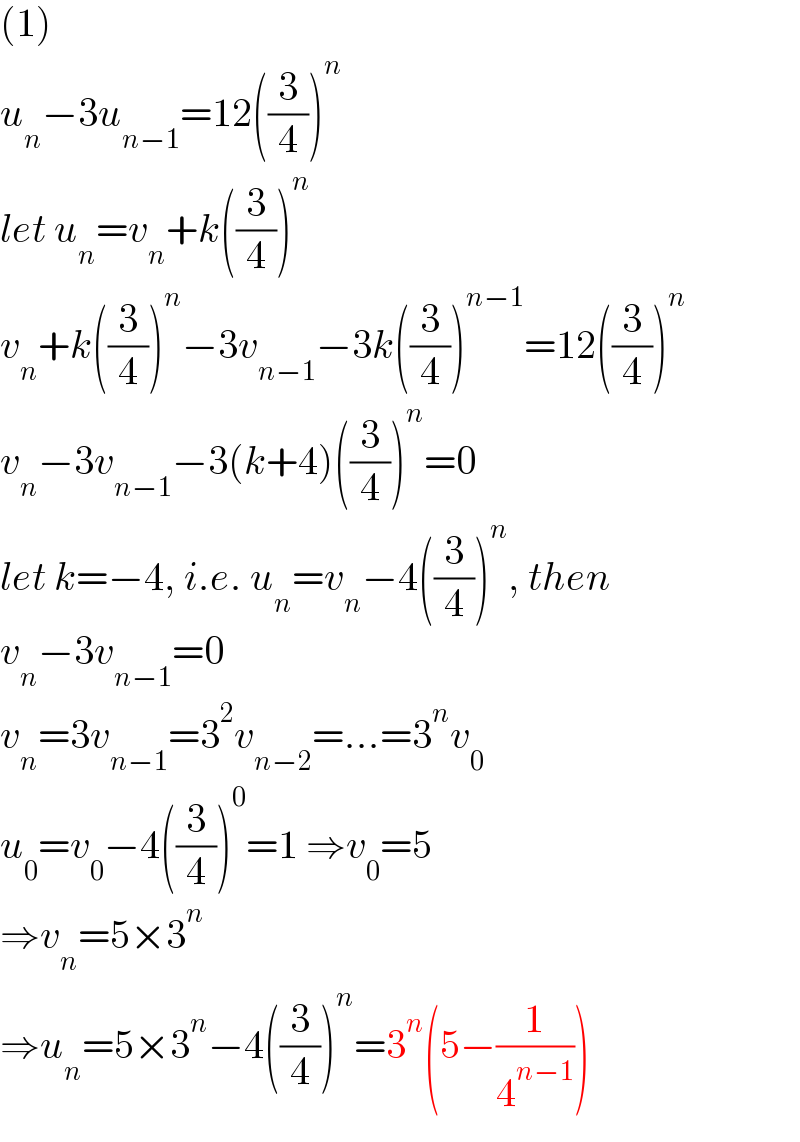
(1) u_n −3u_(n−1) =12((3/4))^n let u_n =v_n +k((3/4))^n v_n +k((3/4))^n −3v_(n−1) −3k((3/4))^(n−1) =12((3/4))^n v_n −3v_(n−1) −3(k+4)((3/4))^n =0 let k=−4, i.e. u_n =v_n −4((3/4))^n , then v_n −3v_(n−1) =0 v_n =3v_(n−1) =3^2 v_(n−2) =...=3^n v_0 u_0 =v_0 −4((3/4))^0 =1 ⇒v_0 =5 ⇒v_n =5×3^n ⇒u_n =5×3^n −4((3/4))^n =3^n (5−(1/4^(n−1) ))
$$\left(\mathrm{1}\right) \\ $$$${u}_{{n}} −\mathrm{3}{u}_{{n}−\mathrm{1}} =\mathrm{12}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} \\ $$$${let}\:{u}_{{n}} ={v}_{{n}} +{k}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} \\ $$$${v}_{{n}} +{k}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} −\mathrm{3}{v}_{{n}−\mathrm{1}} −\mathrm{3}{k}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}−\mathrm{1}} =\mathrm{12}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} \\ $$$${v}_{{n}} −\mathrm{3}{v}_{{n}−\mathrm{1}} −\mathrm{3}\left({k}+\mathrm{4}\right)\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} =\mathrm{0} \\ $$$${let}\:{k}=−\mathrm{4},\:{i}.{e}.\:{u}_{{n}} ={v}_{{n}} −\mathrm{4}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} ,\:{then} \\ $$$${v}_{{n}} −\mathrm{3}{v}_{{n}−\mathrm{1}} =\mathrm{0} \\ $$$${v}_{{n}} =\mathrm{3}{v}_{{n}−\mathrm{1}} =\mathrm{3}^{\mathrm{2}} {v}_{{n}−\mathrm{2}} =…=\mathrm{3}^{{n}} {v}_{\mathrm{0}} \\ $$$${u}_{\mathrm{0}} ={v}_{\mathrm{0}} −\mathrm{4}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{0}} =\mathrm{1}\:\Rightarrow{v}_{\mathrm{0}} =\mathrm{5} \\ $$$$\Rightarrow{v}_{{n}} =\mathrm{5}×\mathrm{3}^{{n}} \\ $$$$\Rightarrow{u}_{{n}} =\mathrm{5}×\mathrm{3}^{{n}} −\mathrm{4}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{n}} =\mathrm{3}^{{n}} \left(\mathrm{5}−\frac{\mathrm{1}}{\mathrm{4}^{{n}−\mathrm{1}} }\right) \\ $$
Commented by Tawa11 last updated on 01/Dec/21
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *