Question Number 168722 by LEKOUMA last updated on 16/Apr/22
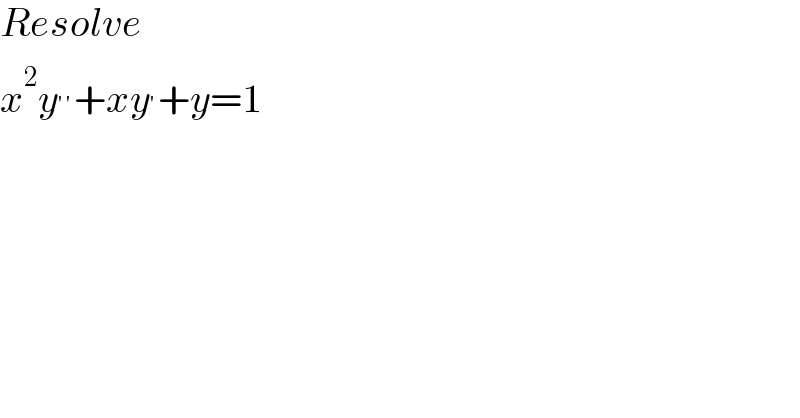
$${Resolve}\: \\ $$$${x}^{\mathrm{2}} {y}^{''} +{xy}^{'} +{y}=\mathrm{1} \\ $$
Commented by mokys last updated on 16/Apr/22
![solution let:z=lnx → x = e^z [ D(D−1)+D + 1 ] y = 1 ( D^2 + 1 ) y = 1 (m^2 +1)=0⇒m=±i y_c = C_1 cos(z) + C_2 sin(z) y_c = C_1 cos(lnx) + C_2 sin(lnx) let:y_p = a → y _p^′ = y _p^(′′) = 0 ∴ 0 + a = 1 ⇒ a=1 ∴ y_p = 1 y = y_c + y_p = C_1 cos(lnx) + C_2 sin(lnx) + 1 ((aldolaimy))](https://www.tinkutara.com/question/Q168735.png)
$${solution} \\ $$$$ \\ $$$${let}:{z}={lnx}\:\rightarrow\:{x}\:=\:{e}^{{z}} \\ $$$$ \\ $$$$\left[\:{D}\left({D}−\mathrm{1}\right)+{D}\:+\:\mathrm{1}\:\right]\:{y}\:=\:\mathrm{1} \\ $$$$ \\ $$$$\:\left(\:{D}^{\mathrm{2}} \:+\:\mathrm{1}\:\right)\:{y}\:=\:\mathrm{1} \\ $$$$ \\ $$$$\left({m}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0}\Rightarrow{m}=\pm{i} \\ $$$$ \\ $$$${y}_{{c}} \:=\:{C}_{\mathrm{1}} {cos}\left({z}\right)\:+\:{C}_{\mathrm{2}} \:{sin}\left({z}\right) \\ $$$$ \\ $$$${y}_{{c}} \:=\:{C}_{\mathrm{1}} \:{cos}\left({lnx}\right)\:+\:{C}_{\mathrm{2}} \:{sin}\left({lnx}\right) \\ $$$$ \\ $$$${let}:{y}_{{p}} \:=\:{a}\:\rightarrow\:{y}\:_{{p}} ^{'} \:=\:{y}\:_{{p}} ^{''} \:=\:\mathrm{0} \\ $$$$ \\ $$$$\therefore\:\mathrm{0}\:+\:{a}\:=\:\mathrm{1}\:\Rightarrow\:{a}=\mathrm{1} \\ $$$$ \\ $$$$\therefore\:{y}_{{p}} \:=\:\mathrm{1} \\ $$$$ \\ $$$${y}\:=\:{y}_{{c}} \:+\:{y}_{{p}} \:=\:{C}_{\mathrm{1}} \:{cos}\left({lnx}\right)\:+\:{C}_{\mathrm{2}} \:{sin}\left({lnx}\right)\:+\:\mathrm{1} \\ $$$$ \\ $$$$\left(\left({aldolaimy}\right)\right) \\ $$$$ \\ $$
