Question Number 168723 by LEKOUMA last updated on 16/Apr/22

$${Resolve}\: \\ $$$$\left({x}+\mathrm{5}\right)^{\mathrm{5}} {y}^{''} =\mathrm{1} \\ $$
Commented by greougoury555 last updated on 16/Apr/22
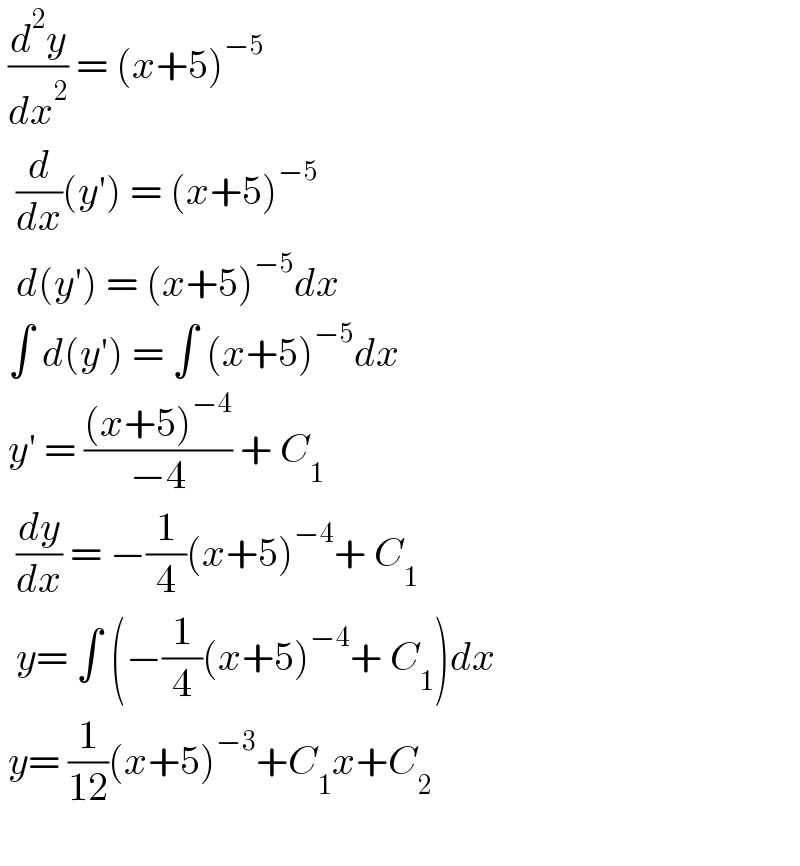
$$\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:\left({x}+\mathrm{5}\right)^{−\mathrm{5}} \\ $$$$\:\:\frac{{d}}{{dx}}\left({y}'\right)\:=\:\left({x}+\mathrm{5}\right)^{−\mathrm{5}} \\ $$$$\:\:{d}\left({y}'\right)\:=\:\left({x}+\mathrm{5}\right)^{−\mathrm{5}} {dx} \\ $$$$\:\int\:{d}\left({y}'\right)\:=\:\int\:\left({x}+\mathrm{5}\right)^{−\mathrm{5}} {dx} \\ $$$$\:{y}'\:=\:\frac{\left({x}+\mathrm{5}\right)^{−\mathrm{4}} }{−\mathrm{4}}\:+\:{C}_{\mathrm{1}} \\ $$$$\:\:\frac{{dy}}{{dx}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\left({x}+\mathrm{5}\right)^{−\mathrm{4}} +\:{C}_{\mathrm{1}} \\ $$$$\:\:{y}=\:\int\:\left(−\frac{\mathrm{1}}{\mathrm{4}}\left({x}+\mathrm{5}\right)^{−\mathrm{4}} +\:{C}_{\mathrm{1}} \right){dx} \\ $$$$\:{y}=\:\frac{\mathrm{1}}{\mathrm{12}}\left({x}+\mathrm{5}\right)^{−\mathrm{3}} +{C}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} \\ $$$$\: \\ $$
Commented by AbdoulayeLelouche last updated on 18/Apr/22

$$\mathrm{very}\:\mathrm{good}. \\ $$
