Question Number 168742 by LEKOUMA last updated on 16/Apr/22
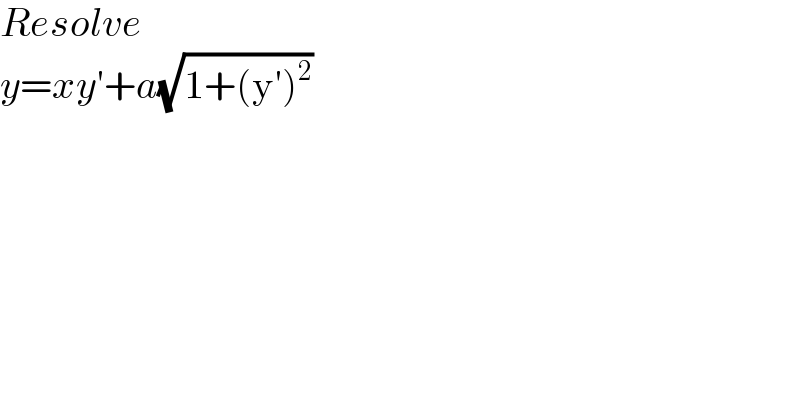
$${Resolve} \\ $$$${y}={xy}'+{a}\sqrt{\mathrm{1}+\left(\mathrm{y}'\right)^{\mathrm{2}} } \\ $$
Answered by mindispower last updated on 19/Apr/22
![⇒ y′=xy′′+y′+a((2y′y′′)/(2(√(1+y′^2 )))) y′=z xz′+((zz′)/( (√(1+z^2 ))))=0 z′(x+a(z/( (√(1+z^2 )))))=0 by continuity⇔ { ((z′=0)),(((z/( (√(1+z^2 ))))=−(1/a)x)) :} z=c or z^2 =x^2 (1+z^2 )⇒z^2 =((((x/a))^2 )/(1−((x/a))^2 )),x∈]−1,1[ z=((−x)/( (√(a^2 −x^2 )))),⇒y=(√(a^2 −x^2 ))+c,a>0 y=((−x^2 )/( (√(a^2 −x^2 ))))+a(√(1+(x^2 /(a^2 −x^2 ))))⇒c=0 cx+d=x(c)+a(√(1+c^2 )) d=a(√(1+c^2 )) S={cx+a(√(1+c^2 )),(√(a^2 −x^2 ))}](https://www.tinkutara.com/question/Q168850.png)
$$\Rightarrow \\ $$$${y}'={xy}''+{y}'+{a}\frac{\mathrm{2}{y}'{y}''}{\mathrm{2}\sqrt{\mathrm{1}+{y}'^{\mathrm{2}} }} \\ $$$${y}'={z} \\ $$$${xz}'+\frac{{zz}'}{\:\sqrt{\mathrm{1}+{z}^{\mathrm{2}} }}=\mathrm{0} \\ $$$${z}'\left({x}+{a}\frac{{z}}{\:\sqrt{\mathrm{1}+{z}^{\mathrm{2}} }}\right)=\mathrm{0} \\ $$$${by}\:{continuity}\Leftrightarrow\begin{cases}{{z}'=\mathrm{0}}\\{\frac{{z}}{\:\sqrt{\mathrm{1}+{z}^{\mathrm{2}} }}=−\frac{\mathrm{1}}{{a}}{x}}\end{cases} \\ $$$${z}={c} \\ $$$$\left.{or}\:\:{z}^{\mathrm{2}} ={x}^{\mathrm{2}} \left(\mathrm{1}+{z}^{\mathrm{2}} \right)\Rightarrow{z}^{\mathrm{2}} =\frac{\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} }{\mathrm{1}−\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} },{x}\in\right]−\mathrm{1},\mathrm{1}\left[\right. \\ $$$${z}=\frac{−{x}}{\:\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }},\Rightarrow{y}=\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }+{c},{a}>\mathrm{0} \\ $$$${y}=\frac{−{x}^{\mathrm{2}} }{\:\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}+{a}\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}\Rightarrow{c}=\mathrm{0} \\ $$$${cx}+{d}={x}\left({c}\right)+{a}\sqrt{\mathrm{1}+{c}^{\mathrm{2}} } \\ $$$${d}={a}\sqrt{\mathrm{1}+{c}^{\mathrm{2}} } \\ $$$${S}=\left\{{cx}+{a}\sqrt{\mathrm{1}+{c}^{\mathrm{2}} },\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\right\} \\ $$$$ \\ $$
