Question Number 180542 by a.lgnaoui last updated on 13/Nov/22

$${Resoudre}\:{dans}\:\mathbb{R} \\ $$$$\left.\mathrm{1}\right) \\ $$$${a}+{b}+{c}=\mathrm{2} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{6} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\left.\mathrm{2}\right) \\ $$$${x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\mathrm{3} \\ $$$${y}^{\mathrm{2}} +{yz}+{z}^{\mathrm{2}} =\mathrm{7} \\ $$$${z}^{\mathrm{2}} +{zx}+{x}^{\mathrm{2}} =\mathrm{13} \\ $$
Answered by mr W last updated on 13/Nov/22
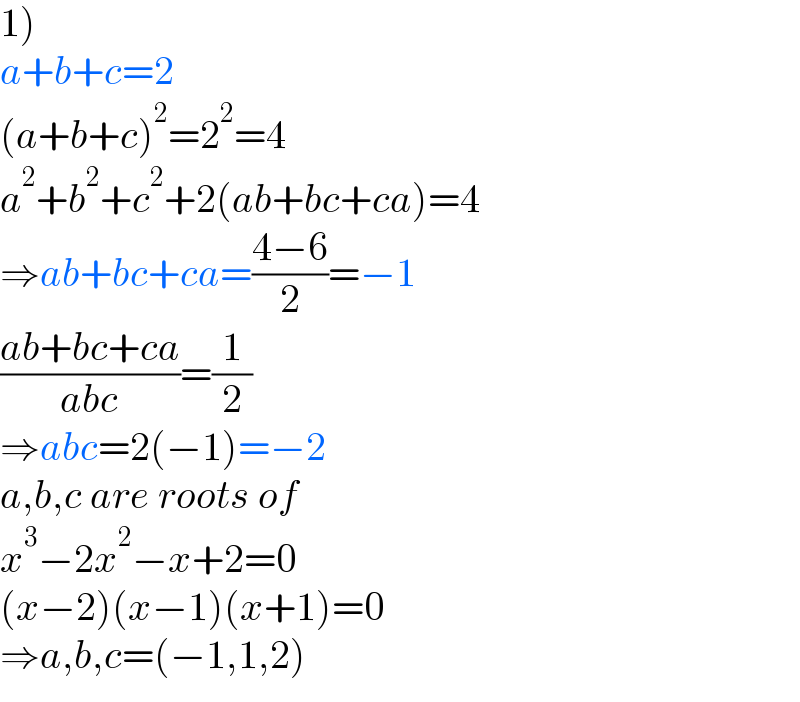
$$\left.\mathrm{1}\right) \\ $$$${a}+{b}+{c}=\mathrm{2} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right)=\mathrm{4} \\ $$$$\Rightarrow{ab}+{bc}+{ca}=\frac{\mathrm{4}−\mathrm{6}}{\mathrm{2}}=−\mathrm{1} \\ $$$$\frac{{ab}+{bc}+{ca}}{{abc}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{abc}=\mathrm{2}\left(−\mathrm{1}\right)=−\mathrm{2} \\ $$$${a},{b},{c}\:{are}\:{roots}\:{of} \\ $$$${x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −{x}+\mathrm{2}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{a},{b},{c}=\left(−\mathrm{1},\mathrm{1},\mathrm{2}\right) \\ $$
Commented by a.lgnaoui last updated on 13/Nov/22

$${thanks}\: \\ $$
Answered by mr W last updated on 14/Nov/22
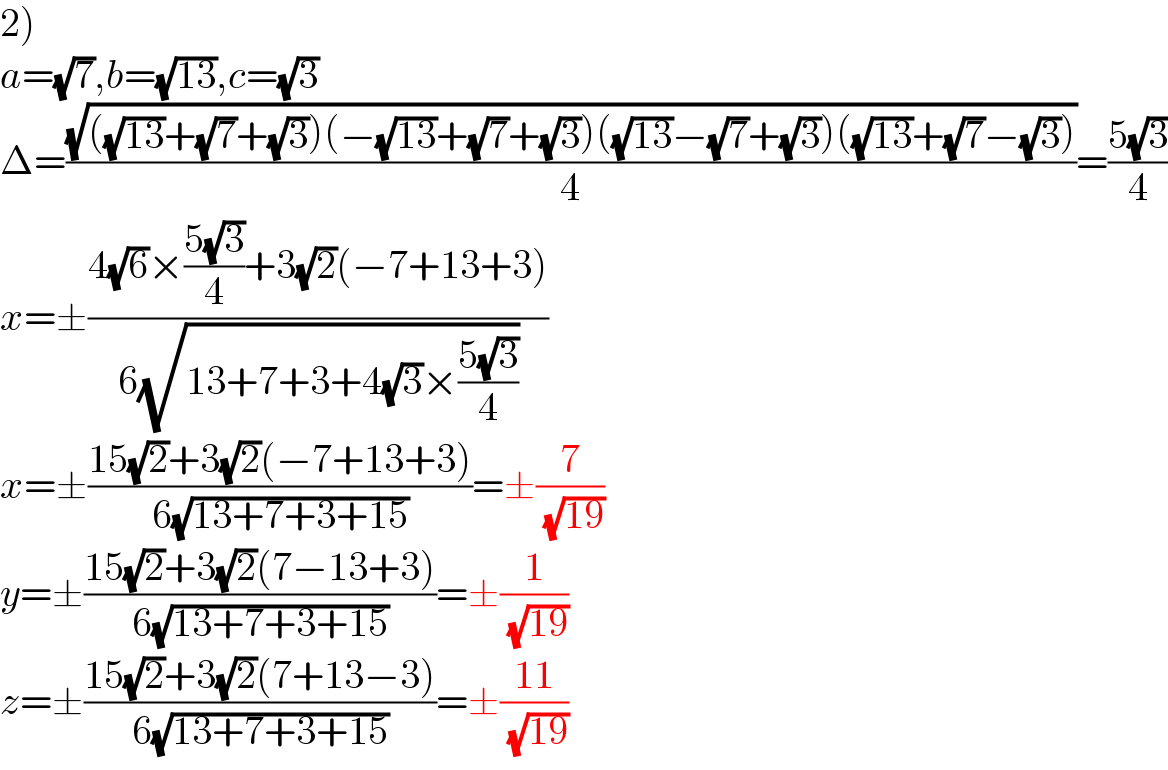
$$\left.\mathrm{2}\right) \\ $$$${a}=\sqrt{\mathrm{7}},{b}=\sqrt{\mathrm{13}},{c}=\sqrt{\mathrm{3}} \\ $$$$\Delta=\frac{\sqrt{\left(\sqrt{\mathrm{13}}+\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}\right)\left(−\sqrt{\mathrm{13}}+\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}\right)\left(\sqrt{\mathrm{13}}−\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}\right)\left(\sqrt{\mathrm{13}}+\sqrt{\mathrm{7}}−\sqrt{\mathrm{3}}\right)}}{\mathrm{4}}=\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$${x}=\pm\frac{\mathrm{4}\sqrt{\mathrm{6}}×\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{4}}+\mathrm{3}\sqrt{\mathrm{2}}\left(−\mathrm{7}+\mathrm{13}+\mathrm{3}\right)}{\mathrm{6}\sqrt{\mathrm{13}+\mathrm{7}+\mathrm{3}+\mathrm{4}\sqrt{\mathrm{3}}×\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{4}}}} \\ $$$${x}=\pm\frac{\mathrm{15}\sqrt{\mathrm{2}}+\mathrm{3}\sqrt{\mathrm{2}}\left(−\mathrm{7}+\mathrm{13}+\mathrm{3}\right)}{\mathrm{6}\sqrt{\mathrm{13}+\mathrm{7}+\mathrm{3}+\mathrm{15}}}=\pm\frac{\mathrm{7}}{\:\sqrt{\mathrm{19}}} \\ $$$${y}=\pm\frac{\mathrm{15}\sqrt{\mathrm{2}}+\mathrm{3}\sqrt{\mathrm{2}}\left(\mathrm{7}−\mathrm{13}+\mathrm{3}\right)}{\mathrm{6}\sqrt{\mathrm{13}+\mathrm{7}+\mathrm{3}+\mathrm{15}}}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{19}}} \\ $$$${z}=\pm\frac{\mathrm{15}\sqrt{\mathrm{2}}+\mathrm{3}\sqrt{\mathrm{2}}\left(\mathrm{7}+\mathrm{13}−\mathrm{3}\right)}{\mathrm{6}\sqrt{\mathrm{13}+\mathrm{7}+\mathrm{3}+\mathrm{15}}}=\pm\frac{\mathrm{11}}{\:\sqrt{\mathrm{19}}} \\ $$
