Question Number 184551 by a.lgnaoui last updated on 08/Jan/23
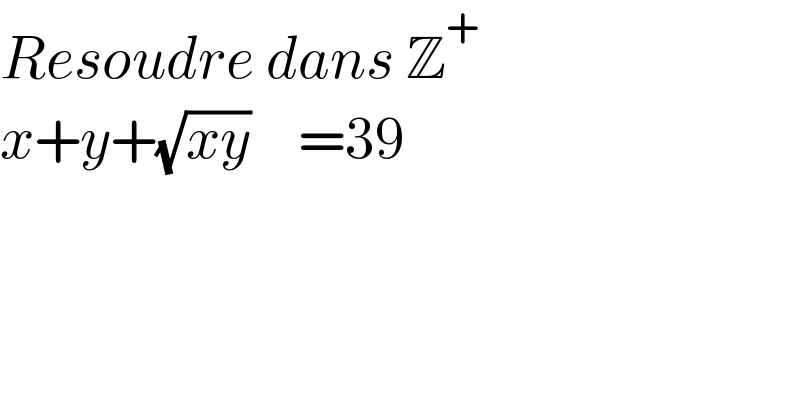
$${Resoudre}\:{dans}\:\mathbb{Z}^{+} \\ $$$${x}+{y}+\sqrt{{xy}}\:\:\:\:=\mathrm{39} \\ $$
Answered by Frix last updated on 08/Jan/23
![xy≥0 ⇒ x≥0∧y≥0∨x<0∧y<0 (1) x<0∧y<0 Let p, q >0∧x=−p^2 ∧y=−q^2 ⇒ p^2 −pq+q^2 +39=0 no real solution (2) x≥0∧y≥0 [⇒ 0≤x, y≤39] Let p, q ≥0∧x=p^2 ∧y=q^2 ⇒ p^2 +pq+q^2 −39=0 ⇒ q=−((p±(√(3(52−p^2 ))))/2) ⇔ y=39−(x/2)−((√(3x(52−x)))/2) [the “+” solution leads to y>39] Following pairs (x, y) and (y, x) are possible: (0, 39) (3, 27) (4, 25) (13, 13)](https://www.tinkutara.com/question/Q184553.png)
$${xy}\geqslant\mathrm{0}\:\Rightarrow\:{x}\geqslant\mathrm{0}\wedge{y}\geqslant\mathrm{0}\vee{x}<\mathrm{0}\wedge{y}<\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:{x}<\mathrm{0}\wedge{y}<\mathrm{0} \\ $$$$\mathrm{Let}\:{p},\:{q}\:>\mathrm{0}\wedge{x}=−{p}^{\mathrm{2}} \wedge{y}=−{q}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${p}^{\mathrm{2}} −{pq}+{q}^{\mathrm{2}} +\mathrm{39}=\mathrm{0}\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution} \\ $$$$\left(\mathrm{2}\right)\:{x}\geqslant\mathrm{0}\wedge{y}\geqslant\mathrm{0}\:\:\:\:\:\left[\Rightarrow\:\mathrm{0}\leqslant{x},\:{y}\leqslant\mathrm{39}\right] \\ $$$$\mathrm{Let}\:{p},\:{q}\:\geqslant\mathrm{0}\wedge{x}={p}^{\mathrm{2}} \wedge{y}={q}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${p}^{\mathrm{2}} +{pq}+{q}^{\mathrm{2}} −\mathrm{39}=\mathrm{0}\:\Rightarrow\:{q}=−\frac{{p}\pm\sqrt{\mathrm{3}\left(\mathrm{52}−{p}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$$\Leftrightarrow \\ $$$${y}=\mathrm{39}−\frac{{x}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}{x}\left(\mathrm{52}−{x}\right)}}{\mathrm{2}}\:\:\:\:\:\left[\mathrm{the}\:“+''\:\mathrm{solution}\:\mathrm{leads}\:\mathrm{to}\:{y}>\mathrm{39}\right] \\ $$$$\mathrm{Following}\:\mathrm{pairs}\:\left({x},\:{y}\right)\:\mathrm{and}\:\left({y},\:{x}\right)\:\mathrm{are}\:\mathrm{possible}: \\ $$$$\left(\mathrm{0},\:\mathrm{39}\right) \\ $$$$\left(\mathrm{3},\:\mathrm{27}\right) \\ $$$$\left(\mathrm{4},\:\mathrm{25}\right) \\ $$$$\left(\mathrm{13},\:\mathrm{13}\right) \\ $$
Commented by a.lgnaoui last updated on 08/Jan/23
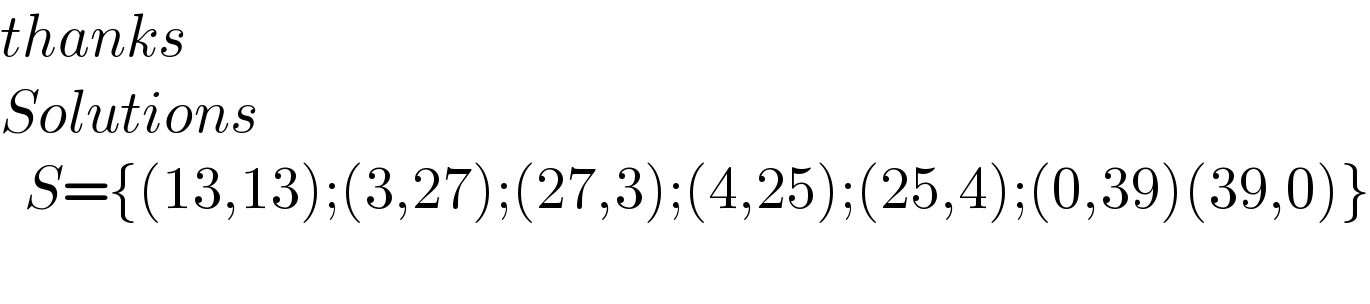
$${thanks} \\ $$$${Solutions}\: \\ $$$$\:\:{S}=\left\{\left(\mathrm{13},\mathrm{13}\right);\left(\mathrm{3},\mathrm{27}\right);\left(\mathrm{27},\mathrm{3}\right);\left(\mathrm{4},\mathrm{25}\right);\left(\mathrm{25},\mathrm{4}\right);\left(\mathrm{0},\mathrm{39}\right)\left(\mathrm{39},\mathrm{0}\right)\right\} \\ $$$$\:\:\: \\ $$
