Menu Close

Resoudre-l-equaation-acos-x-bsin-x-c-a-b-c-R-3-

Tinku Tara 0 Comments
Pin




Question Number 177306 by a.lgnaoui last updated on 03/Oct/22
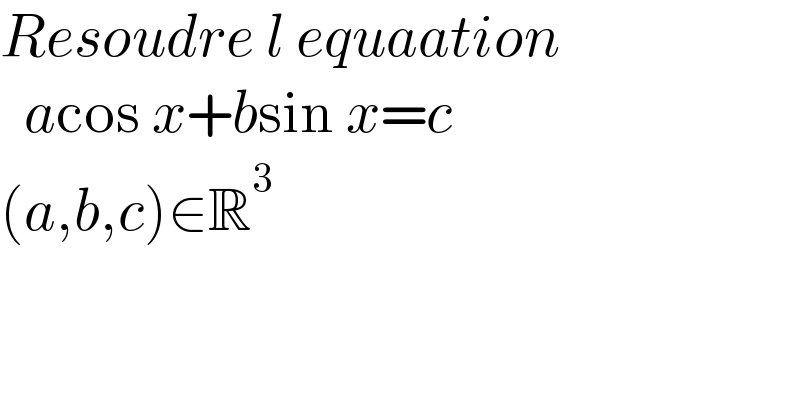
Resoudre l equaation acos x+bsin x=c (a,b,c)∈R^3
$${Resoudre}\:{l}\:{equaation} \\ $$$$\:\:{a}\mathrm{cos}\:{x}+{b}\mathrm{sin}\:{x}={c} \\ $$$$\left({a},{b},{c}\right)\in\mathbb{R}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$
Answered by Ar Brandon last updated on 03/Oct/22
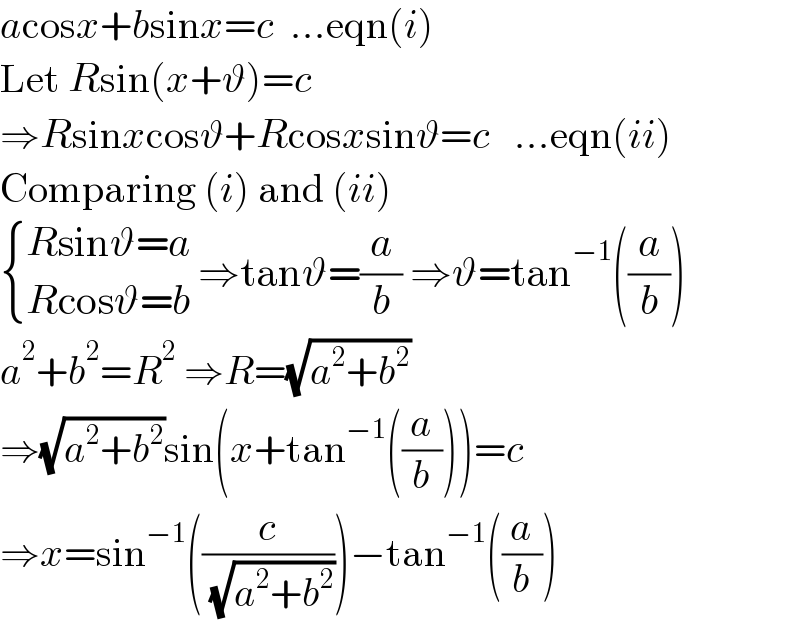
acosx+bsinx=c ...eqn(i) Let Rsin(x+ϑ)=c ⇒Rsinxcosϑ+Rcosxsinϑ=c ...eqn(ii) Comparing (i) and (ii) { ((Rsinϑ=a)),((Rcosϑ=b)) :} ⇒tanϑ=(a/b) ⇒ϑ=tan^(−1) ((a/b)) a^2 +b^2 =R^2 ⇒R=(√(a^2 +b^2 )) ⇒(√(a^2 +b^2 ))sin(x+tan^(−1) ((a/b)))=c ⇒x=sin^(−1) ((c/( (√(a^2 +b^2 )))))−tan^(−1) ((a/b))
$${a}\mathrm{cos}{x}+{b}\mathrm{sin}{x}={c}\:\:…\mathrm{eqn}\left({i}\right) \\ $$$$\mathrm{Let}\:{R}\mathrm{sin}\left({x}+\vartheta\right)={c} \\ $$$$\Rightarrow{R}\mathrm{sin}{x}\mathrm{cos}\vartheta+{R}\mathrm{cos}{x}\mathrm{sin}\vartheta={c}\:\:\:…\mathrm{eqn}\left({ii}\right) \\ $$$$\mathrm{Comparing}\:\left({i}\right)\:\mathrm{and}\:\left({ii}\right) \\ $$$$\begin{cases}{{R}\mathrm{sin}\vartheta={a}}\\{{R}\mathrm{cos}\vartheta={b}}\end{cases}\:\Rightarrow\mathrm{tan}\vartheta=\frac{{a}}{{b}}\:\Rightarrow\vartheta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}}{{b}}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={R}^{\mathrm{2}} \:\Rightarrow{R}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\mathrm{sin}\left({x}+\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}}{{b}}\right)\right)={c} \\ $$$$\Rightarrow{x}=\mathrm{sin}^{−\mathrm{1}} \left(\frac{{c}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}}{{b}}\right) \\ $$
Commented by a.lgnaoui last updated on 03/Oct/22
sin (x+tan^(−1) ((a/b)))=(c/( (√(a^2 +b^2 )))) x+tan^(−1) ((a/b))=sin^(−1) ((c/( (√(a^2 +b^2 ))))) x+α=β⇒x=β−α x=[sin^(−1) ((c/( (√(a^2 +b^2 )))))−tan^(−1) ((a/b))]
$$\mathrm{sin}\:\left({x}+\mathrm{tan}\:^{−\mathrm{1}} \left(\frac{{a}}{{b}}\right)\right)=\frac{{c}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${x}+\mathrm{tan}\:^{−\mathrm{1}} \left(\frac{{a}}{{b}}\right)=\mathrm{sin}^{−\mathrm{1}} \left(\frac{{c}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right) \\ $$$${x}+\alpha=\beta\Rightarrow{x}=\beta−\alpha \\ $$$${x}=\left[\mathrm{sin}\:^{−\mathrm{1}} \left(\frac{{c}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)−\mathrm{tan}\:^{−\mathrm{1}} \left(\frac{{a}}{{b}}\right)\right] \\ $$
Commented by a.lgnaoui last updated on 03/Oct/22
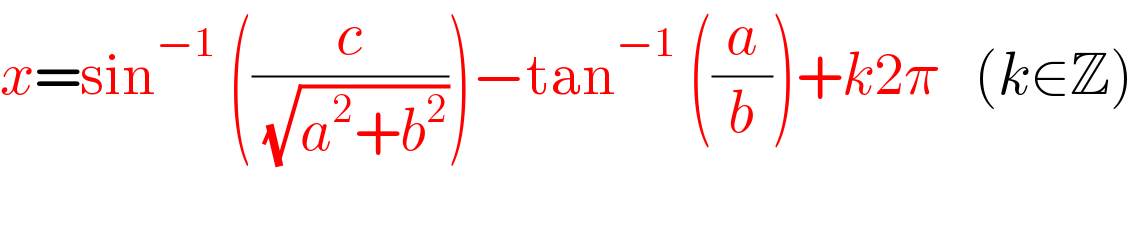
x=sin^(−1) ((c/( (√(a^2 +b^2 )))))−tan^(−1) ((a/b))+k2π (k∈Z)
$${x}=\mathrm{sin}^{−\mathrm{1}} \:\left(\frac{{c}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)−\mathrm{tan}^{−\mathrm{1}} \:\left(\frac{{a}}{{b}}\right)+{k}\mathrm{2}\pi\:\:\:\left({k}\in\mathbb{Z}\right)\: \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 03/Oct/22
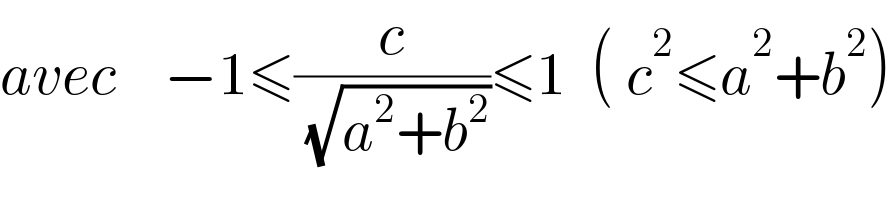
avec −1≤(c/( (√(a^2 +b^2 ))))≤1 ( c^2 ≤a^2 +b^2 )
$${avec}\:\:\:\:−\mathrm{1}\leqslant\frac{{c}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\leqslant\mathrm{1}\:\:\left(\:{c}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$
Answered by a.lgnaoui last updated on 03/Oct/22
on peut poser t=tan (( x)/2) sin x=((2t)/(2+t^2 )) cos x=((1−t^2 )/(1+t^2 )) a(1−t^2 )+2bt=c(1+t^2 ) t^2 −((2b)/(a+c))t+((c−a)/(c+a))=0 Δ′=(b^2 /((a+c)^2 ))−((c−a)/(a+c))=((a^2 +b^2 −c^2 )/((a+c)^2 )) (c^2 ≤a^2 +b^2 ) t=((b±(√(a^2 +b^2 −c^2 )))/(a+c)) (x_1 /2)=Arctan(((b+(√(a^2 +b^2 −c^2 )))/(a+c)) )+(2k+1)π x_1 =2Arctan( ((b+(√(a^2 +b^2 −c^2 )) )/(a+c)))+(2k+1)π (a+c≠0 et k∈Z) x_2 =2Arctan( ((b−(√(a^2 +b^2 −c^2 )))/(a+c)))+(2k+1)π
$${on}\:{peut}\:{poser}\:{t}=\mathrm{tan}\:\frac{\:{x}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:{x}=\frac{\mathrm{2}{t}}{\mathrm{2}+{t}^{\mathrm{2}} }\:\:\:\:\mathrm{cos}\:{x}=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${a}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+\mathrm{2}{bt}={c}\left(\mathrm{1}+{t}^{\mathrm{2}} \right) \\ $$$${t}^{\mathrm{2}} −\frac{\mathrm{2}{b}}{{a}+{c}}{t}+\frac{{c}−{a}}{{c}+{a}}=\mathrm{0} \\ $$$$\Delta'=\frac{{b}^{\mathrm{2}} }{\left({a}+{c}\right)^{\mathrm{2}} }−\frac{{c}−{a}}{{a}+{c}}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\left({a}+{c}\right)^{\mathrm{2}} }\:\:\:\left({c}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$${t}=\frac{{b}\pm\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }}{{a}+{c}} \\ $$$$\:\frac{{x}_{\mathrm{1}} }{\mathrm{2}}={A}\mathrm{rctan}\left(\frac{{b}+\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }}{\mathrm{a}+\mathrm{c}}\:\right)+\left(\mathrm{2k}+\mathrm{1}\right)\pi \\ $$$$\:{x}_{\mathrm{1}} =\mathrm{2}{A}\mathrm{rctan}\left(\:\frac{\mathrm{b}+\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \:}\:}{\mathrm{a}+\mathrm{c}}\right)+\left(\mathrm{2k}+\mathrm{1}\right)\pi\:\:\:\left({a}+{c}\neq\mathrm{0}\:{et}\:{k}\in\mathbb{Z}\right) \\ $$$${x}_{\mathrm{2}} =\mathrm{2}{A}\mathrm{rctan}\left(\:\frac{\mathrm{b}−\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }}{\mathrm{a}+\mathrm{c}}\right)+\left(\mathrm{2k}+\mathrm{1}\right)\pi \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *