Question Number 183835 by a.lgnaoui last updated on 30/Dec/22
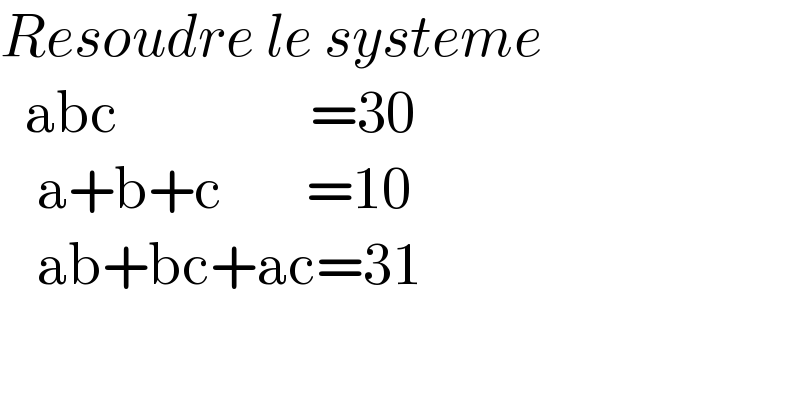
$${Resoudre}\:{le}\:{systeme} \\ $$$$\:\:\mathrm{abc}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{30} \\ $$$$\:\:\:\mathrm{a}+\mathrm{b}+\mathrm{c}\:\:\:\:\:\:\:=\mathrm{10} \\ $$$$\:\:\:\mathrm{ab}+\mathrm{bc}+\mathrm{ac}=\mathrm{31} \\ $$$$ \\ $$
Answered by Frix last updated on 30/Dec/22
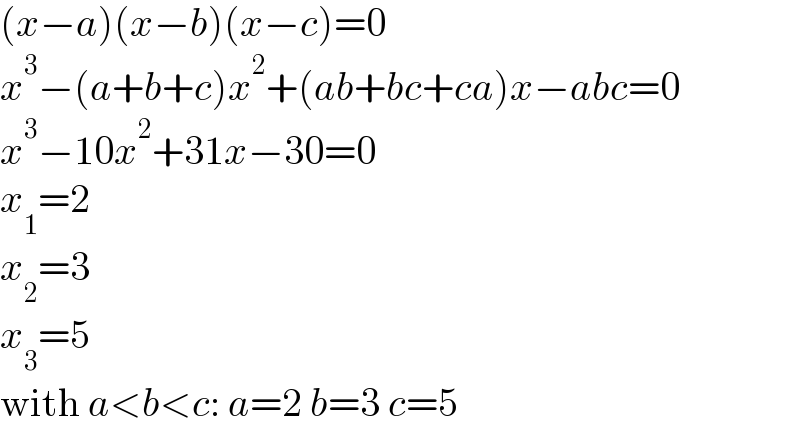
$$\left({x}−{a}\right)\left({x}−{b}\right)\left({x}−{c}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\left({a}+{b}+{c}\right){x}^{\mathrm{2}} +\left({ab}+{bc}+{ca}\right){x}−{abc}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{10}{x}^{\mathrm{2}} +\mathrm{31}{x}−\mathrm{30}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{2} \\ $$$${x}_{\mathrm{2}} =\mathrm{3} \\ $$$${x}_{\mathrm{3}} =\mathrm{5} \\ $$$$\mathrm{with}\:{a}<{b}<{c}:\:{a}=\mathrm{2}\:{b}=\mathrm{3}\:{c}=\mathrm{5} \\ $$
Commented by a.lgnaoui last updated on 30/Dec/22

$${thank}\:{you} \\ $$
Answered by a.lgnaoui last updated on 30/Dec/22
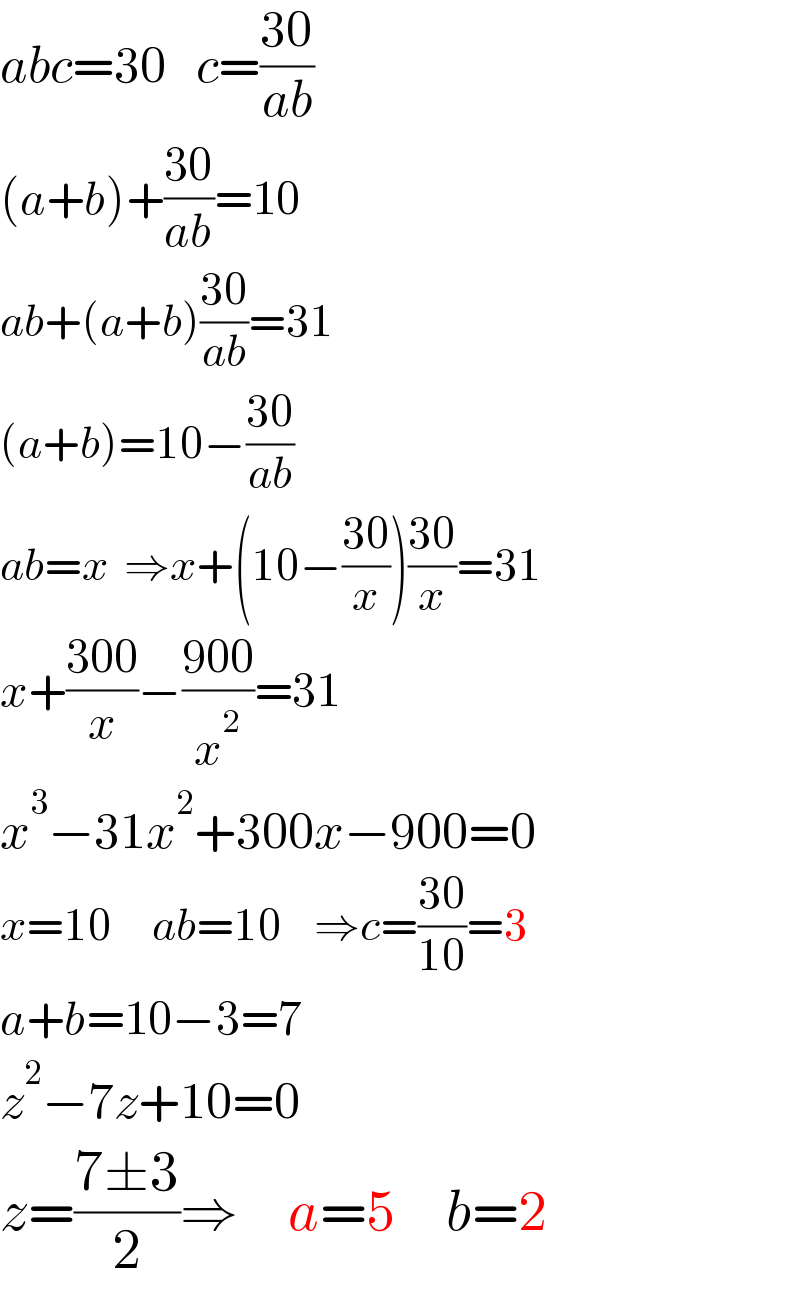
$${abc}=\mathrm{30}\:\:\:{c}=\frac{\mathrm{30}}{{ab}} \\ $$$$\left({a}+{b}\right)+\frac{\mathrm{30}}{{ab}}=\mathrm{10}\:\:\:\: \\ $$$${ab}+\left({a}+{b}\right)\frac{\mathrm{30}}{{ab}}=\mathrm{31} \\ $$$$\left({a}+{b}\right)=\mathrm{10}−\frac{\mathrm{30}}{{ab}} \\ $$$${ab}={x}\:\:\Rightarrow{x}+\left(\mathrm{10}−\frac{\mathrm{30}}{{x}}\right)\frac{\mathrm{30}}{{x}}=\mathrm{31} \\ $$$${x}+\frac{\mathrm{300}}{{x}}−\frac{\mathrm{900}}{{x}^{\mathrm{2}} }=\mathrm{31} \\ $$$${x}^{\mathrm{3}} −\mathrm{31}{x}^{\mathrm{2}} +\mathrm{300}{x}−\mathrm{900}=\mathrm{0} \\ $$$${x}=\mathrm{10}\:\:\:\:\:{ab}=\mathrm{10}\:\:\:\:\Rightarrow{c}=\frac{\mathrm{30}}{\mathrm{10}}=\mathrm{3} \\ $$$${a}+{b}=\mathrm{10}−\mathrm{3}=\mathrm{7}\:\:\:\: \\ $$$${z}^{\mathrm{2}} −\mathrm{7}{z}+\mathrm{10}=\mathrm{0} \\ $$$${z}=\frac{\mathrm{7}\pm\mathrm{3}}{\mathrm{2}}\Rightarrow\:\:\:\:\:{a}=\mathrm{5}\:\:\:\:\:{b}=\mathrm{2} \\ $$
