Menu Close

Rotating-a-curve-y-x-about-the-x-axis-produces-a-head-light-as-shown-below-What-is-the-area-of-disc-at-any-x-

Tinku Tara 0 Comments
Pin




Question Number 15036 by Tinkutara last updated on 07/Jun/17
Rotating a curve y = (√x) about the x- axis produces a “head light” as shown below. What is the area of disc at any x?
$$\mathrm{Rotating}\:\mathrm{a}\:\mathrm{curve}\:{y}\:=\:\sqrt{{x}}\:\mathrm{about}\:\mathrm{the}\:{x}- \\ $$$$\mathrm{axis}\:\mathrm{produces}\:\mathrm{a}\:“\mathrm{head}\:\mathrm{light}''\:\mathrm{as}\:\mathrm{shown} \\ $$$$\mathrm{below}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{disc}\:\mathrm{at}\:\mathrm{any}\:{x}? \\ $$
Commented by Tinkutara last updated on 07/Jun/17
Commented by Tinkutara last updated on 07/Jun/17
In the above problem what is the volume of this head light where x varies from 0 to 2?
$$\mathrm{In}\:\mathrm{the}\:\mathrm{above}\:\mathrm{problem}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{volume}\:\mathrm{of}\:\mathrm{this}\:\mathrm{head}\:\mathrm{light}\:\mathrm{where}\:{x}\:\mathrm{varies} \\ $$$$\mathrm{from}\:\mathrm{0}\:\mathrm{to}\:\mathrm{2}? \\ $$
Answered by ajfour last updated on 07/Jun/17
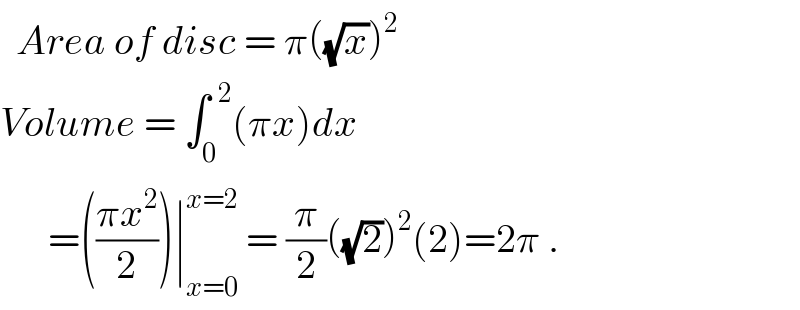
Area of disc = π((√x))^2 Volume = ∫_0 ^( 2) (πx)dx =(((πx^2 )/2))∣_(x=0) ^(x=2) = (π/2)((√2))^2 (2)=2π .
$$\:\:{Area}\:{of}\:{disc}\:=\:\pi\left(\sqrt{{x}}\right)^{\mathrm{2}} \: \\ $$$${Volume}\:=\:\int_{\mathrm{0}} ^{\:\:\mathrm{2}} \left(\pi{x}\right){dx} \\ $$$$\:\:\:\:\:\:=\left(\frac{\pi{x}^{\mathrm{2}} }{\mathrm{2}}\right)\mid_{{x}=\mathrm{0}} ^{{x}=\mathrm{2}} \:=\:\frac{\pi}{\mathrm{2}}\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{2}\right)=\mathrm{2}\pi\:. \\ $$
Commented by Tinkutara last updated on 07/Jun/17
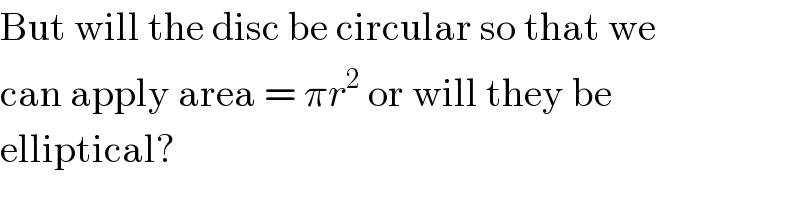
But will the disc be circular so that we can apply area = πr^2 or will they be elliptical?
$$\mathrm{But}\:\mathrm{will}\:\mathrm{the}\:\mathrm{disc}\:\mathrm{be}\:\mathrm{circular}\:\mathrm{so}\:\mathrm{that}\:\mathrm{we} \\ $$$$\mathrm{can}\:\mathrm{apply}\:\mathrm{area}\:=\:\pi{r}^{\mathrm{2}} \:\mathrm{or}\:\mathrm{will}\:\mathrm{they}\:\mathrm{be} \\ $$$$\mathrm{elliptical}? \\ $$
Commented by ajfour last updated on 07/Jun/17
an elementary layer of disc of at location t has its thickness dt and radius (√t) . Its volume will be dV=(Area×thickness) = π((√t))^2 dt to obtain the sum of volumes of such consecutive layers starting at t=0 till t=x , we integrate the expression of dV with limits t=0, to t=x . V (x)=π((t^2 /2))∣_(t=0) ^(t=x) =((πx^2 )/2) .
$${an}\:{elementary}\:{layer}\:{of}\:{disc}\:{of} \\ $$$${at}\:{location}\:{t}\:{has}\:{its}\:{thickness}\:{dt} \\ $$$${and}\:{radius}\:\sqrt{{t}}\:.\:{Its}\:{volume}\:{will}\:{be} \\ $$$${dV}=\left({Area}×{thickness}\right) \\ $$$$\:\:\:\:\:=\:\pi\left(\sqrt{{t}}\right)^{\mathrm{2}} {dt} \\ $$$${to}\:{obtain}\:{the}\:\:{sum}\:{of}\:{volumes} \\ $$$${of}\:{such}\:{consecutive}\:{layers}\:{starting} \\ $$$${at}\:{t}=\mathrm{0}\:{till}\:{t}={x}\:,\:{we}\:{integrate}\:{the} \\ $$$${expression}\:{of}\:{dV}\:\:{with}\:{limits} \\ $$$${t}=\mathrm{0},\:{to}\:\:{t}={x}\:. \\ $$$${V}\:\left({x}\right)=\pi\left(\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right)\mid_{{t}=\mathrm{0}} ^{{t}={x}} \:=\frac{\pi{x}^{\mathrm{2}} }{\mathrm{2}}\:. \\ $$
Commented by ajfour last updated on 07/Jun/17
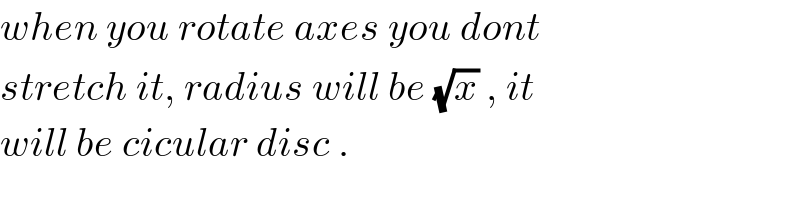
when you rotate axes you dont stretch it, radius will be (√x) , it will be cicular disc .
$${when}\:{you}\:{rotate}\:{axes}\:{you}\:{dont} \\ $$$${stretch}\:{it},\:{radius}\:{will}\:{be}\:\sqrt{{x}}\:,\:{it} \\ $$$${will}\:{be}\:{cicular}\:{disc}\:. \\ $$
Commented by Tinkutara last updated on 07/Jun/17
Thanks Sir!
$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *