Menu Close

S-1-1-10-2-1-10-2-4-1-10-4-8-1-10-8-

Tinku Tara 0 Comments
Pin




Question Number 154328 by liberty last updated on 17/Sep/21
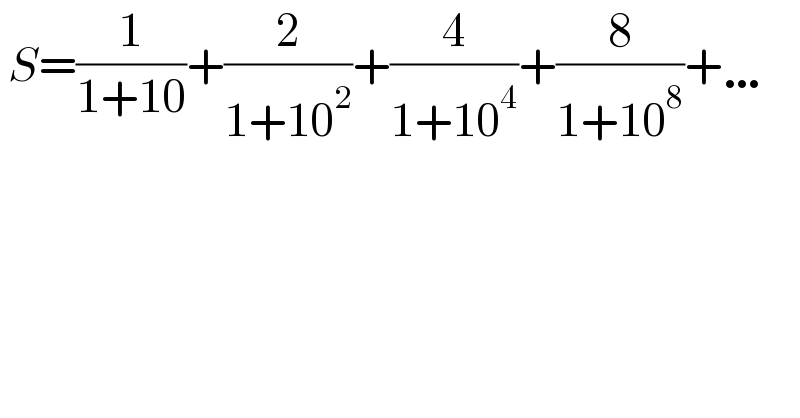
S=(1/(1+10))+(2/(1+10^2 ))+(4/(1+10^4 ))+(8/(1+10^8 ))+…
$$\:{S}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{10}}+\frac{\mathrm{2}}{\mathrm{1}+\mathrm{10}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{1}+\mathrm{10}^{\mathrm{4}} }+\frac{\mathrm{8}}{\mathrm{1}+\mathrm{10}^{\mathrm{8}} }+\ldots\: \\ $$$$ \\ $$
Answered by MJS_new last updated on 17/Sep/21
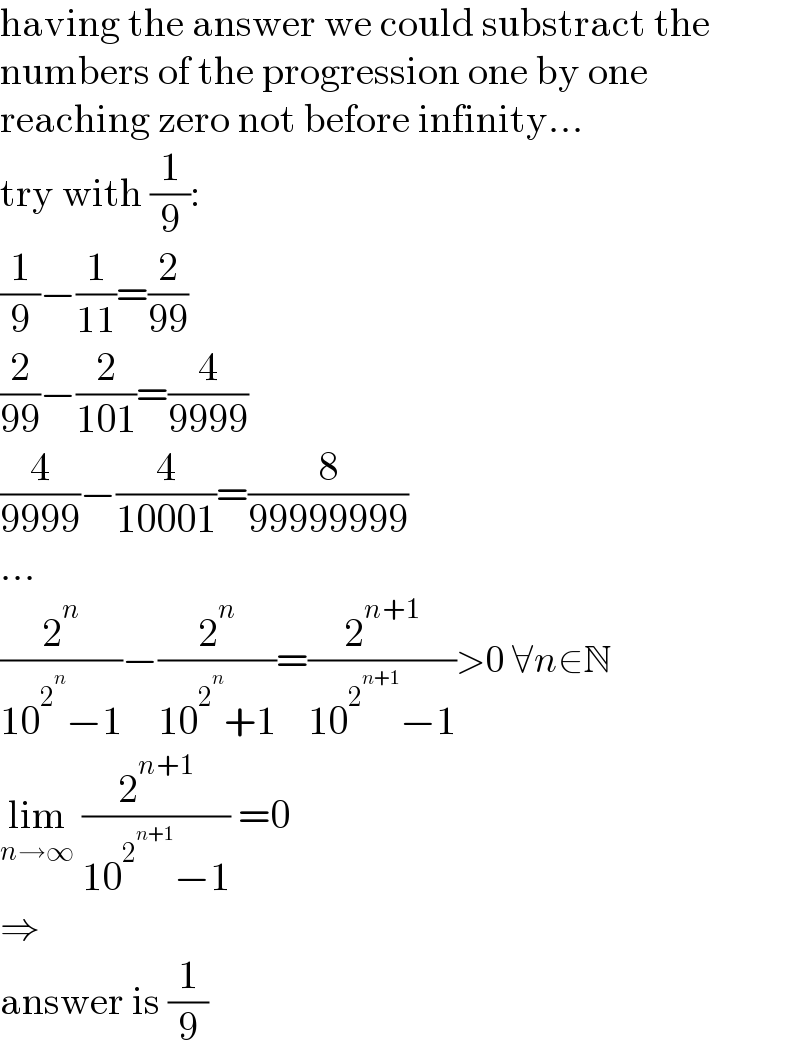
having the answer we could substract the numbers of the progression one by one reaching zero not before infinity... try with (1/9): (1/9)−(1/(11))=(2/(99)) (2/(99))−(2/(101))=(4/(9999)) (4/(9999))−(4/(10001))=(8/(99999999)) ... (2^n /(10^2^n −1))−(2^n /(10^2^n +1))=(2^(n+1) /(10^2^(n+1) −1))>0 ∀n∈N lim_(n→∞) (2^(n+1) /(10^2^(n+1) −1)) =0 ⇒ answer is (1/9)
$$\mathrm{having}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{we}\:\mathrm{could}\:\mathrm{substract}\:\mathrm{the} \\ $$$$\mathrm{numbers}\:\mathrm{of}\:\mathrm{the}\:\mathrm{progression}\:\mathrm{one}\:\mathrm{by}\:\mathrm{one} \\ $$$$\mathrm{reaching}\:\mathrm{zero}\:\mathrm{not}\:\mathrm{before}\:\mathrm{infinity}… \\ $$$$\mathrm{try}\:\mathrm{with}\:\frac{\mathrm{1}}{\mathrm{9}}: \\ $$$$\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{11}}=\frac{\mathrm{2}}{\mathrm{99}} \\ $$$$\frac{\mathrm{2}}{\mathrm{99}}−\frac{\mathrm{2}}{\mathrm{101}}=\frac{\mathrm{4}}{\mathrm{9999}} \\ $$$$\frac{\mathrm{4}}{\mathrm{9999}}−\frac{\mathrm{4}}{\mathrm{10001}}=\frac{\mathrm{8}}{\mathrm{99999999}} \\ $$$$… \\ $$$$\frac{\mathrm{2}^{{n}} }{\mathrm{10}^{\mathrm{2}^{{n}} } −\mathrm{1}}−\frac{\mathrm{2}^{{n}} }{\mathrm{10}^{\mathrm{2}^{{n}} } +\mathrm{1}}=\frac{\mathrm{2}^{{n}+\mathrm{1}} }{\mathrm{10}^{\mathrm{2}^{{n}+\mathrm{1}} } −\mathrm{1}}>\mathrm{0}\:\forall{n}\in\mathbb{N} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{2}^{{n}+\mathrm{1}} }{\mathrm{10}^{\mathrm{2}^{{n}+\mathrm{1}} } −\mathrm{1}}\:=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{9}} \\ $$
Commented by peter frank last updated on 17/Sep/21
more clarification please
$$\mathrm{more}\:\mathrm{clarification}\:\mathrm{please} \\ $$
Commented by liberty last updated on 17/Sep/21
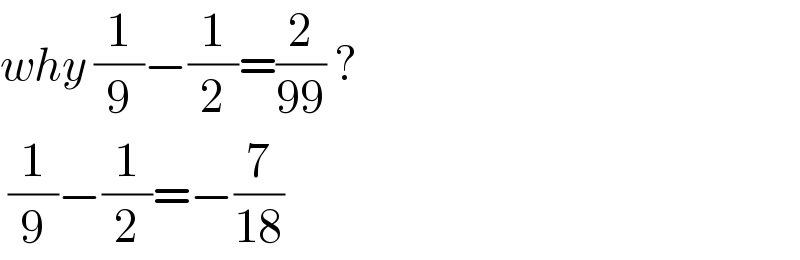
why (1/9)−(1/2)=(2/(99)) ? (1/9)−(1/2)=−(7/(18))
$${why}\:\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{99}}\:? \\ $$$$\:\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{7}}{\mathrm{18}}\: \\ $$
Commented by MJS_new last updated on 17/Sep/21
sorry typo
$$\mathrm{sorry}\:\mathrm{typo} \\ $$
Commented by MJS_new last updated on 17/Sep/21
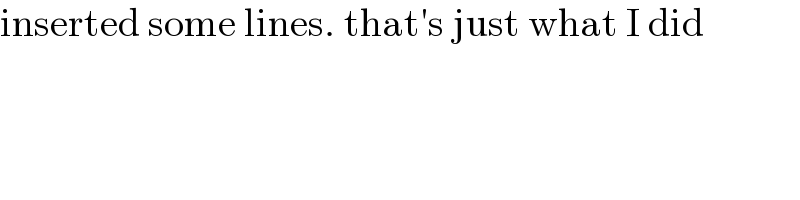
inserted some lines. that′s just what I did
$$\mathrm{inserted}\:\mathrm{some}\:\mathrm{lines}.\:\mathrm{that}'\mathrm{s}\:\mathrm{just}\:\mathrm{what}\:\mathrm{I}\:\mathrm{did} \\ $$
Answered by EDWIN88 last updated on 17/Sep/21
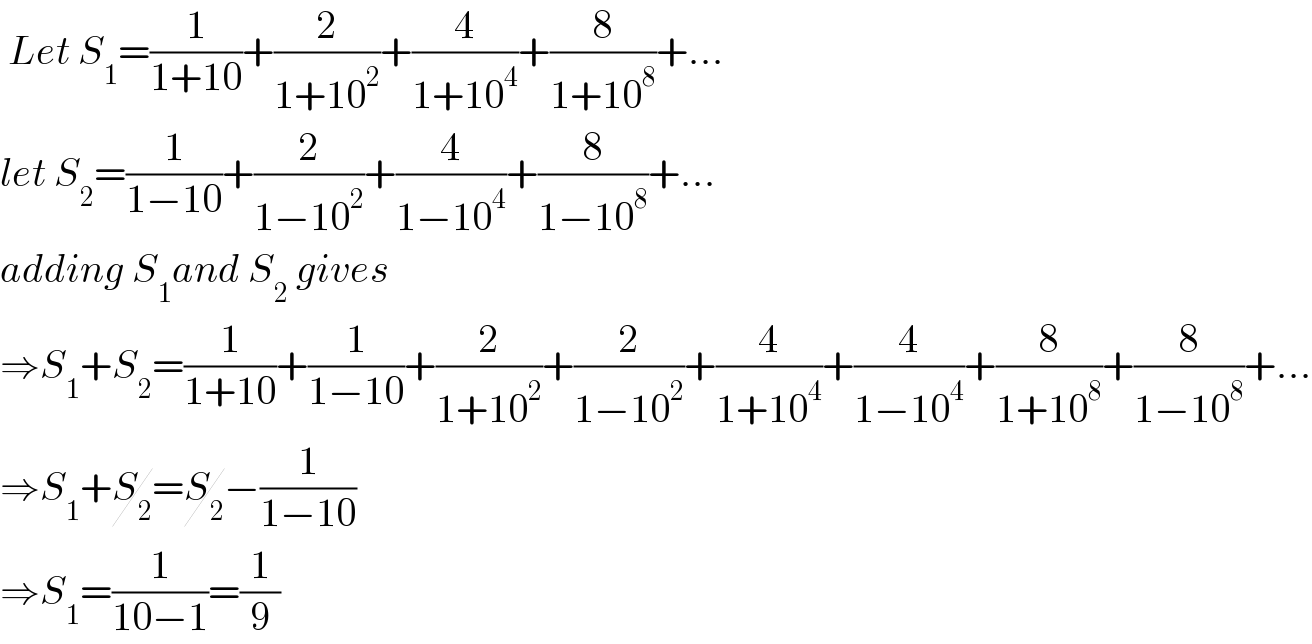
Let S_1 =(1/(1+10))+(2/(1+10^2 ))+(4/(1+10^4 ))+(8/(1+10^8 ))+... let S_2 =(1/(1−10))+(2/(1−10^2 ))+(4/(1−10^4 ))+(8/(1−10^8 ))+... adding S_1 and S_2 gives ⇒S_1 +S_2 =(1/(1+10))+(1/(1−10))+(2/(1+10^2 ))+(2/(1−10^2 ))+(4/(1+10^4 ))+(4/(1−10^4 ))+(8/(1+10^8 ))+(8/(1−10^8 ))+... ⇒S_1 +S_2 =S_2 −(1/(1−10)) ⇒S_1 =(1/(10−1))=(1/9)
$$\:{Let}\:{S}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}+\mathrm{10}}+\frac{\mathrm{2}}{\mathrm{1}+\mathrm{10}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{1}+\mathrm{10}^{\mathrm{4}} }+\frac{\mathrm{8}}{\mathrm{1}+\mathrm{10}^{\mathrm{8}} }+… \\ $$$${let}\:{S}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{1}−\mathrm{10}}+\frac{\mathrm{2}}{\mathrm{1}−\mathrm{10}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{1}−\mathrm{10}^{\mathrm{4}} }+\frac{\mathrm{8}}{\mathrm{1}−\mathrm{10}^{\mathrm{8}} }+… \\ $$$${adding}\:{S}_{\mathrm{1}} {and}\:{S}_{\mathrm{2}} \:{gives} \\ $$$$\Rightarrow{S}_{\mathrm{1}} +{S}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{1}+\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{10}}+\frac{\mathrm{2}}{\mathrm{1}+\mathrm{10}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{1}−\mathrm{10}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{1}+\mathrm{10}^{\mathrm{4}} }+\frac{\mathrm{4}}{\mathrm{1}−\mathrm{10}^{\mathrm{4}} }+\frac{\mathrm{8}}{\mathrm{1}+\mathrm{10}^{\mathrm{8}} }+\frac{\mathrm{8}}{\mathrm{1}−\mathrm{10}^{\mathrm{8}} }+… \\ $$$$\Rightarrow{S}_{\mathrm{1}} +\cancel{{S}_{\mathrm{2}} }=\cancel{{S}_{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{10}} \\ $$$$\Rightarrow{S}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{10}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *