Question Number 61613 by naka3546 last updated on 05/Jun/19
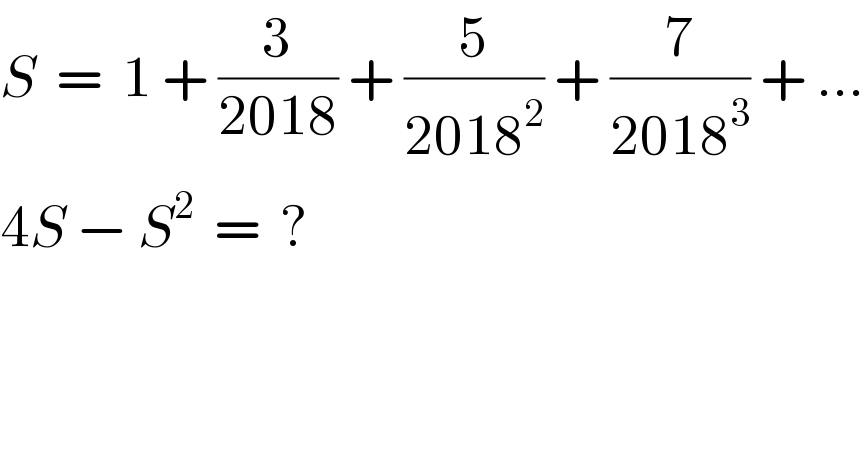
$${S}\:\:=\:\:\mathrm{1}\:+\:\frac{\mathrm{3}}{\mathrm{2018}}\:+\:\frac{\mathrm{5}}{\mathrm{2018}^{\mathrm{2}} }\:+\:\frac{\mathrm{7}}{\mathrm{2018}^{\mathrm{3}} }\:+\:… \\ $$$$\mathrm{4}{S}\:−\:{S}^{\mathrm{2}} \:\:=\:\:? \\ $$
Commented by maxmathsup by imad last updated on 05/Jun/19
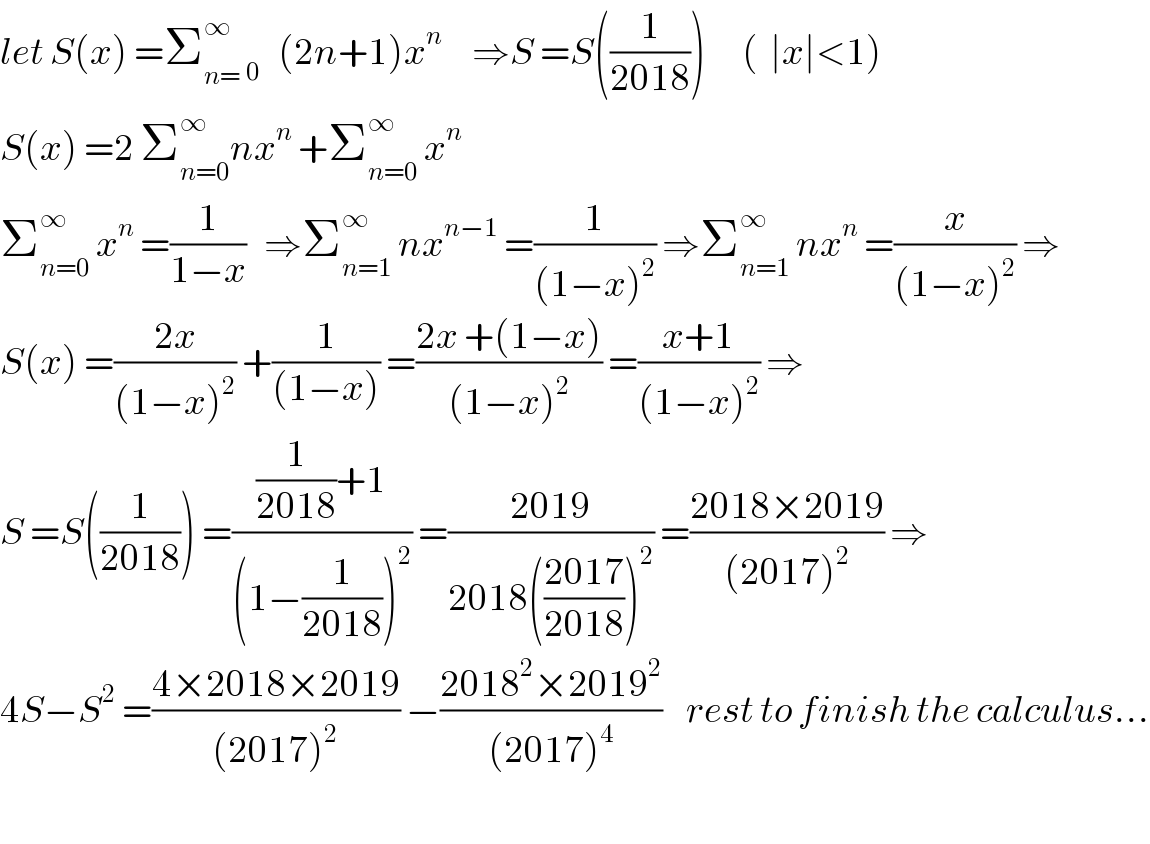
$${let}\:{S}\left({x}\right)\:=\sum_{{n}=} ^{\infty} \:_{\mathrm{0}} \:\:\:\left(\mathrm{2}{n}+\mathrm{1}\right){x}^{{n}} \:\:\:\:\:\Rightarrow{S}\:={S}\left(\frac{\mathrm{1}}{\mathrm{2018}}\right)\:\:\:\:\:\:\left(\:\:\mid{x}\mid<\mathrm{1}\right) \\ $$$${S}\left({x}\right)\:=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} {nx}^{{n}} \:+\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\:\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}−\mathrm{1}} \:=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}} \:=\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${S}\left({x}\right)\:=\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)}\:=\frac{\mathrm{2}{x}\:+\left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:=\frac{{x}+\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${S}\:={S}\left(\frac{\mathrm{1}}{\mathrm{2018}}\right)\:=\frac{\frac{\mathrm{1}}{\mathrm{2018}}+\mathrm{1}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2018}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2019}}{\mathrm{2018}\left(\frac{\mathrm{2017}}{\mathrm{2018}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2018}×\mathrm{2019}}{\left(\mathrm{2017}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{4}{S}−{S}^{\mathrm{2}} \:=\frac{\mathrm{4}×\mathrm{2018}×\mathrm{2019}}{\left(\mathrm{2017}\right)^{\mathrm{2}} }\:−\frac{\mathrm{2018}^{\mathrm{2}} ×\mathrm{2019}^{\mathrm{2}} }{\left(\mathrm{2017}\right)^{\mathrm{4}} }\:\:\:\:{rest}\:{to}\:{finish}\:{the}\:{calculus}… \\ $$$$ \\ $$
Answered by ajfour last updated on 05/Jun/19
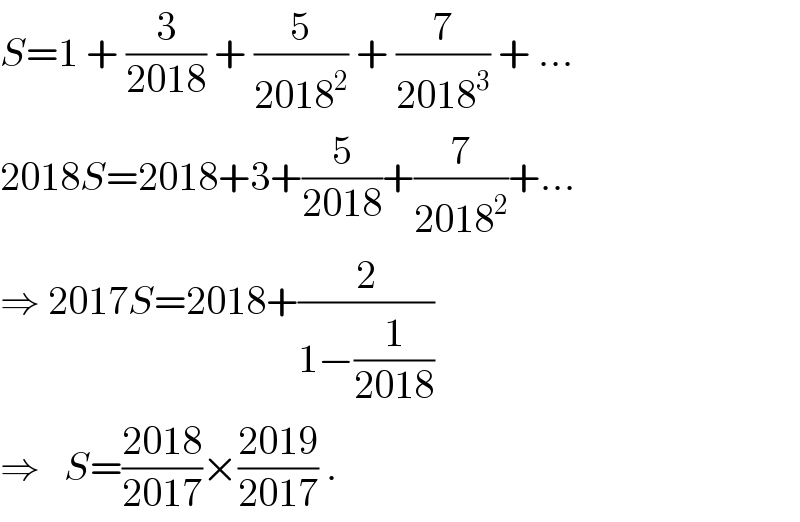
$${S}=\mathrm{1}\:+\:\frac{\mathrm{3}}{\mathrm{2018}}\:+\:\frac{\mathrm{5}}{\mathrm{2018}^{\mathrm{2}} }\:+\:\frac{\mathrm{7}}{\mathrm{2018}^{\mathrm{3}} }\:+\:… \\ $$$$\mathrm{2018}{S}=\mathrm{2018}+\mathrm{3}+\frac{\mathrm{5}}{\mathrm{2018}}+\frac{\mathrm{7}}{\mathrm{2018}^{\mathrm{2}} }+… \\ $$$$\Rightarrow\:\mathrm{2017}{S}=\mathrm{2018}+\frac{\mathrm{2}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2018}}} \\ $$$$\Rightarrow\:\:\:{S}=\frac{\mathrm{2018}}{\mathrm{2017}}×\frac{\mathrm{2019}}{\mathrm{2017}}\:. \\ $$
