Menu Close

s-2-11-0-6-11-10-11-2-14-11-3-18-11-4-s-

Tinku Tara 0 Comments
Pin




Question Number 184927 by mathlove last updated on 14/Jan/23
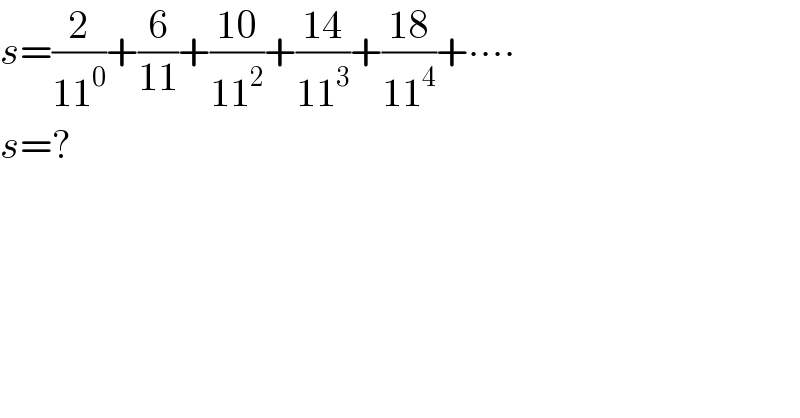
s=(2/(11^0 ))+(6/(11))+((10)/(11^2 ))+((14)/(11^3 ))+((18)/(11^4 ))+∙∙∙∙ s=?
$${s}=\frac{\mathrm{2}}{\mathrm{11}^{\mathrm{0}} }+\frac{\mathrm{6}}{\mathrm{11}}+\frac{\mathrm{10}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{14}}{\mathrm{11}^{\mathrm{3}} }+\frac{\mathrm{18}}{\mathrm{11}^{\mathrm{4}} }+\centerdot\centerdot\centerdot\centerdot \\ $$$${s}=? \\ $$
Answered by Rasheed.Sindhi last updated on 14/Jan/23
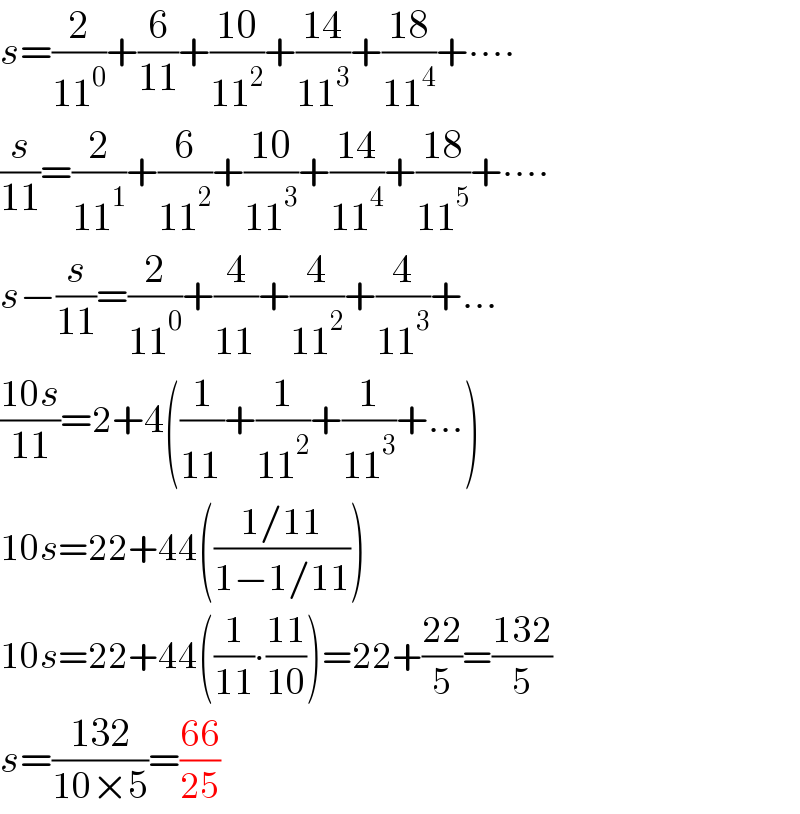
s=(2/(11^0 ))+(6/(11))+((10)/(11^2 ))+((14)/(11^3 ))+((18)/(11^4 ))+∙∙∙∙ (s/(11))=(2/(11^1 ))+(6/(11^2 ))+((10)/(11^3 ))+((14)/(11^4 ))+((18)/(11^5 ))+∙∙∙∙ s−(s/(11))=(2/(11^0 ))+(4/(11^ ))+(4/(11^2 ))+(4/(11^3 ))+... ((10s)/(11))=2+4((1/(11^ ))+(1/(11^2 ))+(1/(11^3 ))+...) 10s=22+44(((1/11)/(1−1/11))) 10s=22+44((1/(11))∙((11)/(10)))=22+((22)/5)=((132)/5) s=((132)/(10×5))=((66)/(25))
$${s}=\frac{\mathrm{2}}{\mathrm{11}^{\mathrm{0}} }+\frac{\mathrm{6}}{\mathrm{11}}+\frac{\mathrm{10}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{14}}{\mathrm{11}^{\mathrm{3}} }+\frac{\mathrm{18}}{\mathrm{11}^{\mathrm{4}} }+\centerdot\centerdot\centerdot\centerdot \\ $$$$\frac{{s}}{\mathrm{11}}=\frac{\mathrm{2}}{\mathrm{11}^{\mathrm{1}} }+\frac{\mathrm{6}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{10}}{\mathrm{11}^{\mathrm{3}} }+\frac{\mathrm{14}}{\mathrm{11}^{\mathrm{4}} }+\frac{\mathrm{18}}{\mathrm{11}^{\mathrm{5}} }+\centerdot\centerdot\centerdot\centerdot \\ $$$${s}−\frac{{s}}{\mathrm{11}}=\frac{\mathrm{2}}{\mathrm{11}^{\mathrm{0}} }+\frac{\mathrm{4}}{\mathrm{11}^{\:} }+\frac{\mathrm{4}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{11}^{\mathrm{3}} }+… \\ $$$$\frac{\mathrm{10}{s}}{\mathrm{11}}=\mathrm{2}+\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{11}^{\:} }+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{3}} }+…\right) \\ $$$$\mathrm{10}{s}=\mathrm{22}+\mathrm{44}\left(\frac{\mathrm{1}/\mathrm{11}}{\mathrm{1}−\mathrm{1}/\mathrm{11}}\right) \\ $$$$\mathrm{10}{s}=\mathrm{22}+\mathrm{44}\left(\frac{\mathrm{1}}{\mathrm{11}}\centerdot\frac{\mathrm{11}}{\mathrm{10}}\right)=\mathrm{22}+\frac{\mathrm{22}}{\mathrm{5}}=\frac{\mathrm{132}}{\mathrm{5}} \\ $$$${s}=\frac{\mathrm{132}}{\mathrm{10}×\mathrm{5}}=\frac{\mathrm{66}}{\mathrm{25}} \\ $$
Commented by mathlove last updated on 14/Jan/23
thanks dear
$${thanks}\:{dear} \\ $$
Answered by Rasheed.Sindhi last updated on 14/Jan/23
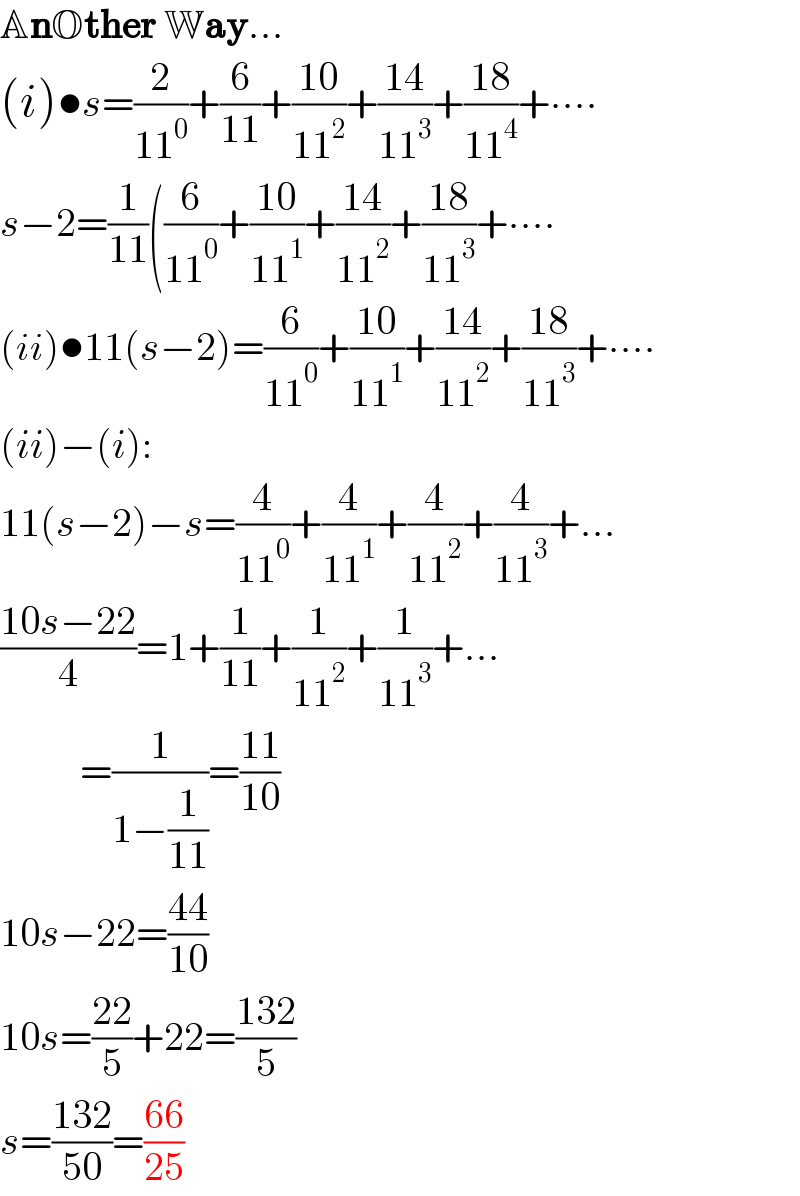
AnOther Way... (i)•s=(2/(11^0 ))+(6/(11))+((10)/(11^2 ))+((14)/(11^3 ))+((18)/(11^4 ))+∙∙∙∙ s−2=(1/(11))((6/(11^0 ))+((10)/(11^1 ))+((14)/(11^2 ))+((18)/(11^3 ))+∙∙∙∙ (ii)•11(s−2)=(6/(11^0 ))+((10)/(11^1 ))+((14)/(11^2 ))+((18)/(11^3 ))+∙∙∙∙ (ii)−(i): 11(s−2)−s=(4/(11^0 ))+(4/(11^1 ))+(4/(11^2 ))+(4/(11^3 ))+... ((10s−22)/4)=1+(1/(11))+(1/(11^2 ))+(1/(11^3 ))+... =(1/(1−(1/(11))))=((11)/(10)) 10s−22=((44)/(10)) 10s=((22)/5)+22=((132)/5) s=((132)/(50))=((66)/(25))
$$\mathbb{A}\boldsymbol{\mathrm{n}}\mathbb{O}\boldsymbol{\mathrm{ther}}\:\mathbb{W}\boldsymbol{\mathrm{ay}}… \\ $$$$\left({i}\right)\bullet{s}=\frac{\mathrm{2}}{\mathrm{11}^{\mathrm{0}} }+\frac{\mathrm{6}}{\mathrm{11}}+\frac{\mathrm{10}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{14}}{\mathrm{11}^{\mathrm{3}} }+\frac{\mathrm{18}}{\mathrm{11}^{\mathrm{4}} }+\centerdot\centerdot\centerdot\centerdot \\ $$$${s}−\mathrm{2}=\frac{\mathrm{1}}{\mathrm{11}}\left(\frac{\mathrm{6}}{\mathrm{11}^{\mathrm{0}} }+\frac{\mathrm{10}}{\mathrm{11}^{\mathrm{1}} }+\frac{\mathrm{14}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{18}}{\mathrm{11}^{\mathrm{3}} }+\centerdot\centerdot\centerdot\centerdot\right. \\ $$$$\left({ii}\right)\bullet\mathrm{11}\left({s}−\mathrm{2}\right)=\frac{\mathrm{6}}{\mathrm{11}^{\mathrm{0}} }+\frac{\mathrm{10}}{\mathrm{11}^{\mathrm{1}} }+\frac{\mathrm{14}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{18}}{\mathrm{11}^{\mathrm{3}} }+\centerdot\centerdot\centerdot\centerdot \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$$\mathrm{11}\left({s}−\mathrm{2}\right)−{s}=\frac{\mathrm{4}}{\mathrm{11}^{\mathrm{0}} }+\frac{\mathrm{4}}{\mathrm{11}^{\mathrm{1}} }+\frac{\mathrm{4}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{11}^{\mathrm{3}} }+… \\ $$$$\frac{\mathrm{10}{s}−\mathrm{22}}{\mathrm{4}}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{11}}+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{3}} }+… \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{11}}}=\frac{\mathrm{11}}{\mathrm{10}} \\ $$$$\mathrm{10}{s}−\mathrm{22}=\frac{\mathrm{44}}{\mathrm{10}} \\ $$$$\mathrm{10}{s}=\frac{\mathrm{22}}{\mathrm{5}}+\mathrm{22}=\frac{\mathrm{132}}{\mathrm{5}} \\ $$$${s}=\frac{\mathrm{132}}{\mathrm{50}}=\frac{\mathrm{66}}{\mathrm{25}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *