Question Number 30860 by ajfour last updated on 27/Feb/18
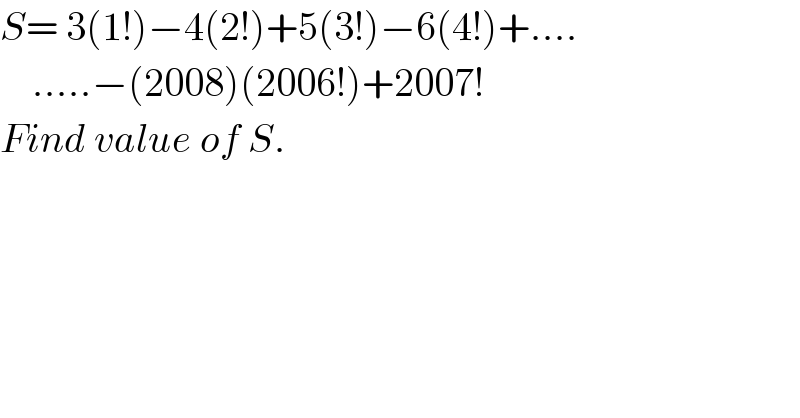
$${S}=\:\mathrm{3}\left(\mathrm{1}!\right)−\mathrm{4}\left(\mathrm{2}!\right)+\mathrm{5}\left(\mathrm{3}!\right)−\mathrm{6}\left(\mathrm{4}!\right)+…. \\ $$$$\:\:\:\:…..−\left(\mathrm{2008}\right)\left(\mathrm{2006}!\right)+\mathrm{2007}! \\ $$$${Find}\:{value}\:{of}\:{S}. \\ $$
Answered by MJS last updated on 27/Feb/18
![3∙1!−4∙2!=−5 [=−(3!−1)] ...+5∙3!=25 [=4!+1] ...−6∙4!=−119 [=−(5!−1)] ...+7∙5!=721 [=6!+1] ... ...−2008∙2006!=−(2007!−1) ...+2007!=1](https://www.tinkutara.com/question/Q30868.png)
$$\mathrm{3}\centerdot\mathrm{1}!−\mathrm{4}\centerdot\mathrm{2}!=−\mathrm{5}\:\left[=−\left(\mathrm{3}!−\mathrm{1}\right)\right] \\ $$$$…+\mathrm{5}\centerdot\mathrm{3}!=\mathrm{25}\:\left[=\mathrm{4}!+\mathrm{1}\right] \\ $$$$…−\mathrm{6}\centerdot\mathrm{4}!=−\mathrm{119}\:\left[=−\left(\mathrm{5}!−\mathrm{1}\right)\right] \\ $$$$…+\mathrm{7}\centerdot\mathrm{5}!=\mathrm{721}\:\left[=\mathrm{6}!+\mathrm{1}\right] \\ $$$$… \\ $$$$…−\mathrm{2008}\centerdot\mathrm{2006}!=−\left(\mathrm{2007}!−\mathrm{1}\right) \\ $$$$…+\mathrm{2007}!=\mathrm{1} \\ $$
Commented by ajfour last updated on 27/Feb/18

$${Great}!\:{Thanks}. \\ $$
