Question Number 148821 by vvvv last updated on 31/Jul/21
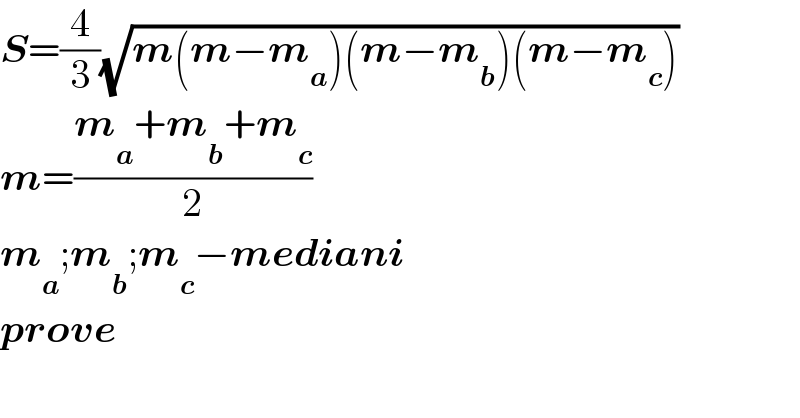
$$\boldsymbol{{S}}=\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\boldsymbol{{m}}\left(\boldsymbol{{m}}−\boldsymbol{{m}}_{\boldsymbol{{a}}} \right)\left(\boldsymbol{{m}}−\boldsymbol{{m}}_{\boldsymbol{{b}}} \right)\left(\boldsymbol{{m}}−\boldsymbol{{m}}_{\boldsymbol{{c}}} \right)} \\ $$$$\boldsymbol{{m}}=\frac{\boldsymbol{{m}}_{\boldsymbol{{a}}} +\boldsymbol{{m}}_{\boldsymbol{{b}}} +\boldsymbol{{m}}_{\boldsymbol{{c}}} }{\mathrm{2}} \\ $$$$\boldsymbol{{m}}_{\boldsymbol{{a}}} ;\boldsymbol{{m}}_{\boldsymbol{{b}}} ;\boldsymbol{{m}}_{\boldsymbol{{c}}} −\boldsymbol{{mediani}} \\ $$$$\boldsymbol{{prove}} \\ $$
Answered by mr W last updated on 31/Jul/21
Commented by mr W last updated on 01/Aug/21

$${i}\:{don}'{t}\:{know}. \\ $$
Commented by mr W last updated on 31/Jul/21
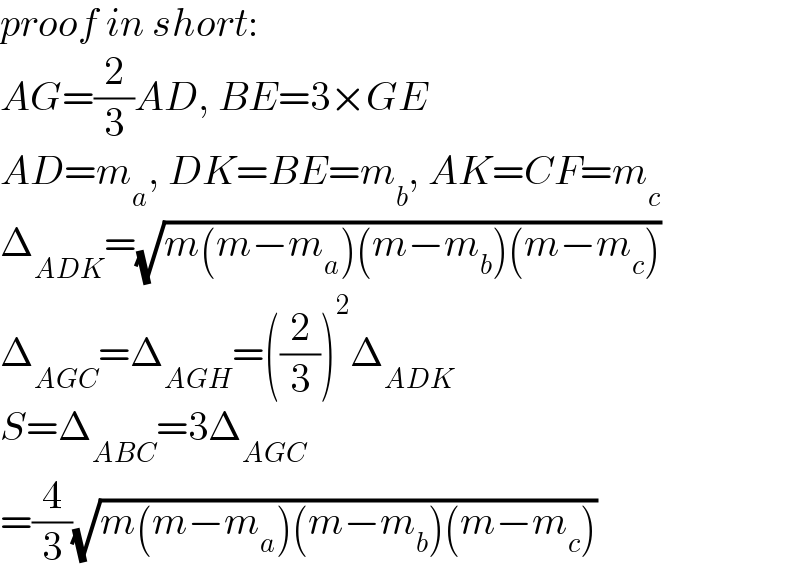
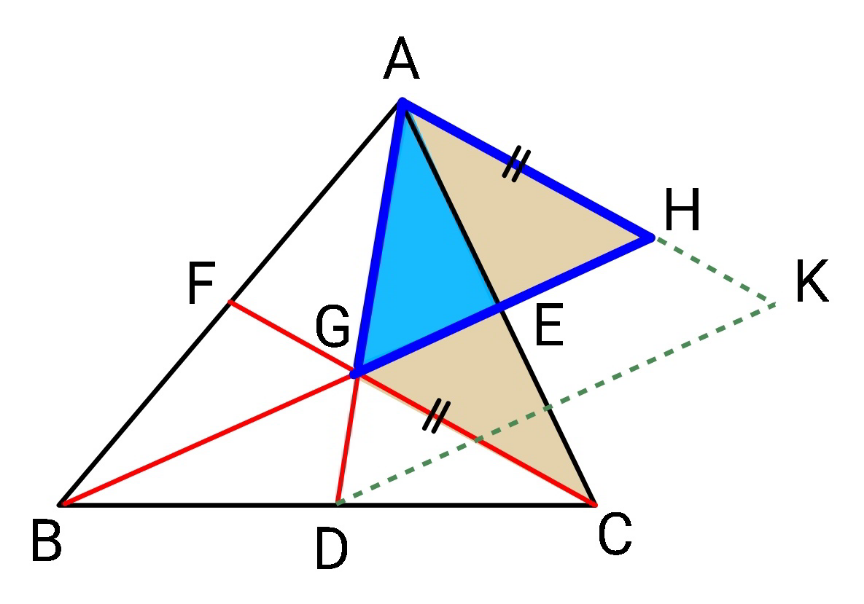
$${proof}\:{in}\:{short}: \\ $$$${AG}=\frac{\mathrm{2}}{\mathrm{3}}{AD},\:{BE}=\mathrm{3}×{GE} \\ $$$${AD}={m}_{{a}} ,\:{DK}={BE}={m}_{{b}} ,\:{AK}={CF}={m}_{{c}} \\ $$$$\Delta_{{ADK}} =\sqrt{{m}\left({m}−{m}_{{a}} \right)\left({m}−{m}_{{b}} \right)\left({m}−{m}_{{c}} \right)} \\ $$$$\Delta_{{AGC}} =\Delta_{{AGH}} =\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} \Delta_{{ADK}} \\ $$$${S}=\Delta_{{ABC}} =\mathrm{3}\Delta_{{AGC}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\sqrt{{m}\left({m}−{m}_{{a}} \right)\left({m}−{m}_{{b}} \right)\left({m}−{m}_{{c}} \right)} \\ $$
Commented by vvvv last updated on 31/Jul/21
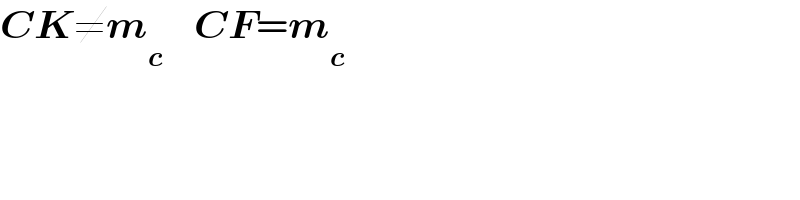
$$\boldsymbol{{CK}}\neq\boldsymbol{{m}}_{\boldsymbol{{c}}} \:\:\:\:\boldsymbol{{CF}}=\boldsymbol{{m}}_{\boldsymbol{{c}}} \\ $$
Commented by vvvv last updated on 31/Jul/21
$${draw}\:{software}\:{name}\:{please} \\ $$
Commented by mr W last updated on 31/Jul/21
$${LEKH}\:{DIAGRAM} \\ $$
Commented by EDWIN88 last updated on 01/Aug/21

$${compatible}\:{to}\:{pc}? \\ $$
